精准获取信息正确解答考题

崔恒刘

解答“统计与概率”方面的考题，关键是通过阅读题目，获取尽可能多的信息，然后利用获取的信息进行解答。下面以部分2018中考题为例，归纳、分析几类给出信息的方式，以帮助同学们提高获取数据信息的能力。

一、文字语言

例1（2018·江苏南京）甲口袋中有2个白球、1个红球，乙口袋中有1个白球、1个红球，这些球除颜色外无其他差别，分别从每个口袋中随机摸出一个球。

（1）求摸出的2个球都是白球的概率。

（2）下列事件中，概率最大的是（ ）。

A.摸出的2个球颜色相同

B.摸出的2个球颜色不相同

C.摸出的2个球中至少有1个红球

D.摸出的2个球中至少有1个白球

【解析】（1）把甲口袋中的2个白球、1个红球分别记为白1、白2、红1，乙口袋中1个白球、1个红球分别记为白3、红2，利用列举法得到所有可能的结果，再根据概率公式计算；（2）分别计算四个选项所对应事件的概率，再比较即可。

解：（1）把甲口袋中的2个白球、1个红球分别记为白1、白2、红1，乙口袋中1个白球、1个红球分别记为白3、红2，分别从每个口袋中随机摸出一个球，所有可能的结果有：（白1，白3），（白1，红2），（白2，白3），（白2，红2），（红1，白3），（红1，红2），共有6 种等可能的结果，其中摸出的2个球都是白球的结果有2种，∴P（摸出的2个球都是白球）

二、平面图形

例2（2018·甘肃武威）如图，在正方形方格中，阴影部分是涂黑3个小正方形所形成的图案。

（1）如果将一粒米随机地抛在这个正方形方格上，那么米粒落在阴影部分的概率是多少？

（2）现将方格内空白的小正方形（A、B、C、D、E、F）中任取2个涂黑，得到新图案。请用列表或画树状图的方法求新图案是轴对称图形的概率。

【解析】（1）阴影部分的面积占总面积的比例即为所求的概率；（2）利用列表或者树状图得到涂黑两个空白的所有情况，再根据轴对称图形定义，得到新图案是轴对称图形的情况数，即可求出概率。

解：（1）米粒落在阴影部分的概率

（2）列表：

共有30种等可能的情况，其中新图案是轴对称图形的有10种，故图案是轴对称图形的概率注：画树状图或列表正确均可得分。）

三、表格

例3（2018·广西桂林）某校为了解高一年级住校学生在校期间的月生活支出情况，从高一年级600名住校生中随机抽取部分学生，对他们今年4月份的生活支出情况进行调查统计，并绘制成如下的统计图表。

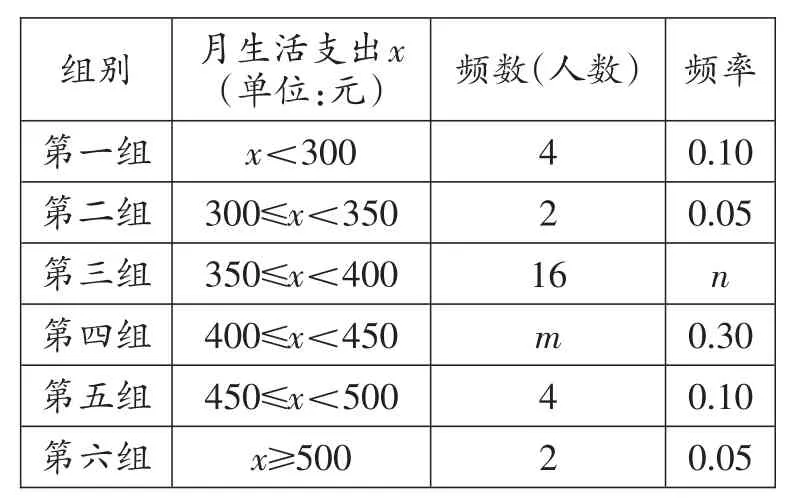
请根据图表中所给的信息，解答下列问题：

（1）这次调查共随机抽取了________名学生，图表中的m=_______，n=_______。

（2）请估计该校高一年级600名住校学生中今年4月份生活支出低于350元的学生人数。

（3）现有一些爱心人士有意愿资助该校家庭困难的学生，学校在本次调查的基础上，经过进一步核实，确定高一（2）班有A、B、C三名学生家庭困难，其中A、B为女生，C为男生。李阿姨申请资助他们中的两名，于是学校让李阿姨从A、B、C三名学生中依次随机抽取两名学生进行资助，请用列表法（或树状图法）求恰好抽到A、B两名女生的概率。

【解析】（1）由第一组的频数、频率可求得总人数，进而求得m、n的值。（2）用第一、二组的频率之和乘600即可求解。（3）可列表或画树状图求出所有可能出现的结果，然后再根据图表中的信息计算概率。

解：（1）4÷0.10=40（名），这次调查共随机抽取了40名学生。m=40×0.30=120.40。

（2）600×（0.10+0.05）=90（人）。所以该校高一今年4月份生活支出低于350元的学生有90人。

（3）列表如下：

画树状图如下：

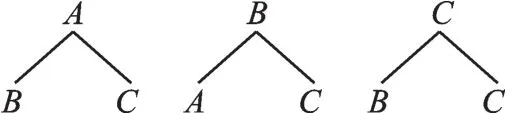
由列表或树状图可知，所有等可能的情况共有6种，其中恰好抽到A、B两名女生的结果有2种，所以恰好抽到A、B两名女生的概率

四、折线统计图和表格

例4（2018·山东菏泽）为了发展学生的核心素养，培养学生的综合能力，某中学利用“阳光大课间”，组织学生积极参加丰富多彩的课外活动，学校成立了舞蹈队、足球队、篮球队、毽子队、射击队等，其中射击队在某次训练中，甲、乙两名队员各射击10发子弹，成绩用下面的折线统计图表示：（甲为实线，乙为虚线）

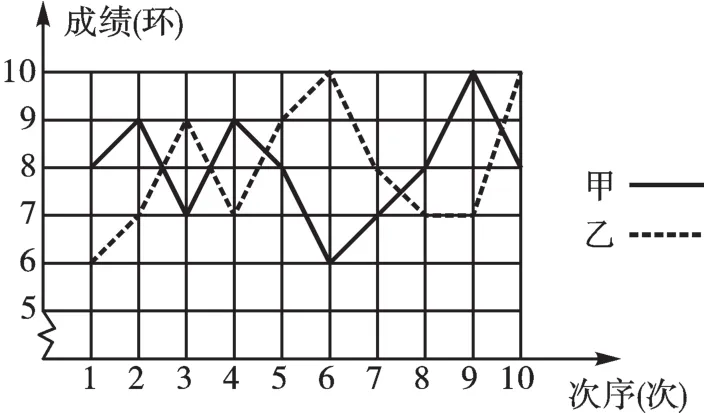
（1）依据折线统计图，得到下面的表格：

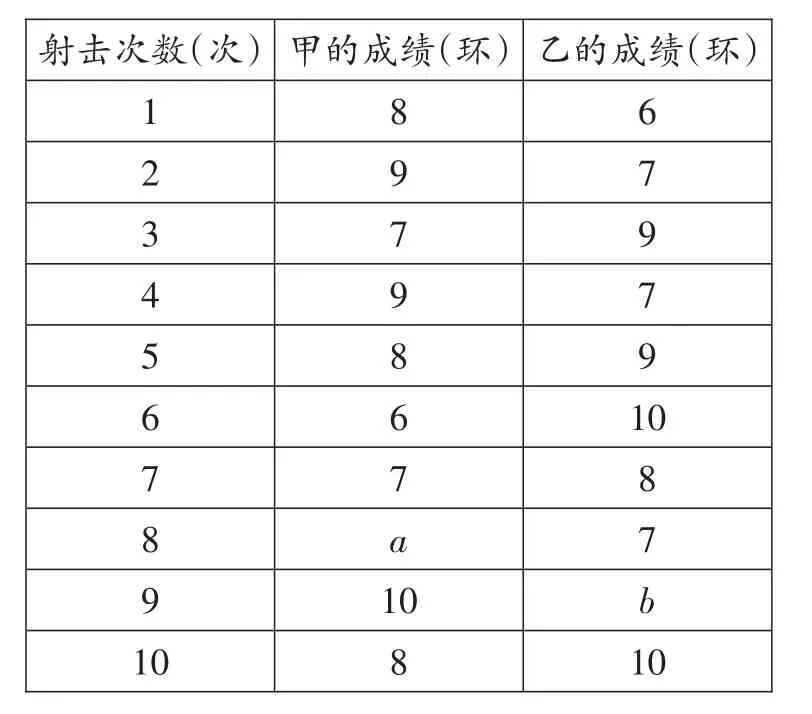
其中a=_______，b=_______。

（2）甲成绩的众数是_______环，乙成绩的中位数是_______环。

（3）请运用方差的知识，判断甲、乙两人谁的成绩更为稳定？

（4）该校射击队要参加市组织的射击比赛，已预选出2名男同学和2名女同学，现要从这4名同学中任意选取2名同学参加比赛，请用列表或画树状图法，求出恰好选到1男1女的概率。

【解析】（1）根据折线图标注的数据信息直接得到a与b的值。（2）甲的十次射击成绩中，出现次数最多的数字即为这组数据的众数；把乙的十次射击成绩按大小顺序排列，处于中间的第5、6个数的平均数即为中位数。（3）利用方差公式计算这两组数据的方差，方差小的成绩更为稳定。（4）利用树状图或列表，找出随机选中两人的所有情况数，再确定1男1女的情况数，利用概率公式计算结果。

（4）画树状图如下：

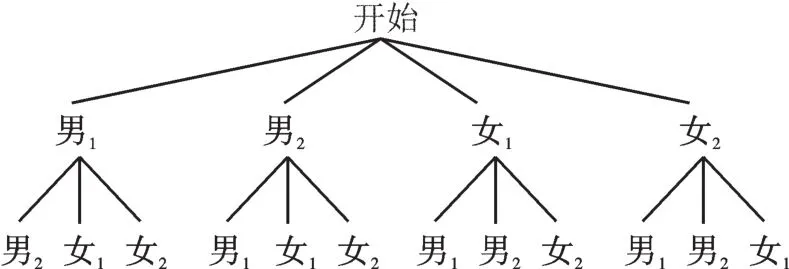
共有12种结果，符合条件的结果有8种，所以，恰好选到1男1女的概率列表（略）。

五、表格和条形图

例5（2018·山东淄博）“推进全科阅读，培育时代新人”。某学校为了更好地开展学生读书节活动，随机调查了八年级50名学生最近一周的读书时间，统计数据如下表：

（1）写出这50名学生最近一周读书时间的众数、中位数、平均数。

（2）根据上述表格补全下面的条形统计图：

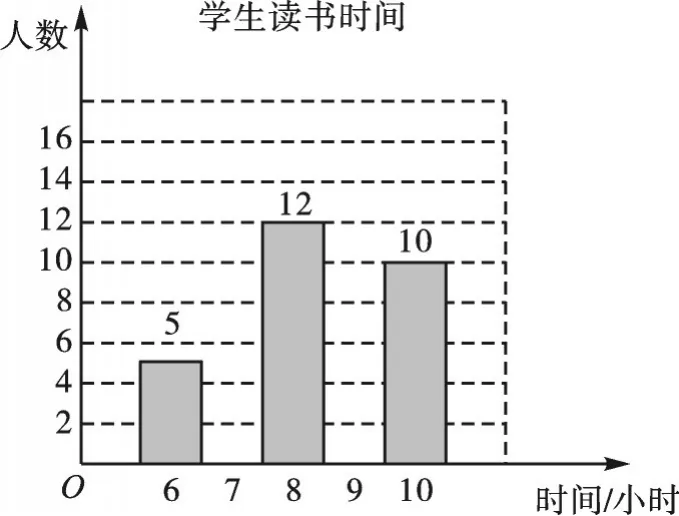
（3）学校从这50名学生中，随机抽取1名学生参加上级部门组织的读书活动，其中被抽到学生的读书时间不少于9小时的概率是多少？

【解析】（1）分别按照三类数的定义解答；（2）依据表格数据补图；（3）利用概率公式计算。

解：（1）众数是：9。中位数是=8.5。平均数是（6×5+7×8+8×12+9×15+10×10）=8.34（小时）。

（2）补全条形统计图：

从上面列举的例题中，我们可以发现：统计与概率方面的题目大多都有生活背景，这体现出“数学来源于生活”的道理。我们在平时的学习中也要多关注生活，学会用所学知识解决生活、学习中的实际问题，提高自己的问题意识、应用意识。