探究“概率”中考考点

程 辉

考点1 判定确定事件与随机事件

例1（2018·福建）投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则下列事件为随机事件的是（ ）。

A.两枚骰子向上一面的点数之和大于1

B.两枚骰子向上一面的点数之和等于1

C.两枚骰子向上一面的点数之和大于12

D.两枚骰子向上一面的点数之和等于12

【解析】投掷两枚质地均匀的骰子，骰子的六个面上分别刻有1到6的点数，则两枚骰子向上一面的点数之和可能是2、3、4、5、6、7、8、9、10、11、12。因此A为必然事件，B、C为不可能事件，D是随机事件。

答案：D。

【点评】此题主要考查随机事件，解题关键是掌握随机事件定义。事先能肯定它一定会发生的事件称为必然事件；事先能肯定它一定不会发生的事件称为不可能事件；在一定条件下，可能发生，也可能不发生的事件，称为随机事件。

考点2 用列表法或树状图法求概率

例2（2018·江苏南通）一个不透明的口袋中有三个完全相同的小球，把他们分别标号1、2、3。随机摸取一个小球，然后放回，再随机摸出一个小球，用列表或画树状图的方法，求两次取出的小球标号相同的概率。

【解析】根据题意画出如下树状图：

从树状图可以看出，可能出现的结果共有9种，并且它们出现的可能性相等，其中两次取出的小球标号相同的结果共有3种。

例3（2018·江苏盐城）端午节是我国传统佳节，小峰带了4个粽子（除粽馅不同外，其他均相同），其中有两个肉馅粽子，一个红枣馅粽子和一个豆沙馅粽子，准备从中任意拿出两个送给他的好朋友小悦。

（1）用树状图或列表的方法列出小悦拿到两个粽子的所有可能结果。

（2）请你计算小悦拿到的两个粽子都是肉馅的概率。

【解析】（1）根据题意画出如下树状图：

由树状图可知：小悦拿到两个粽子的所有可能结果共有12种。

（2）由树状图可知：小悦拿到的两个粽子都是肉馅的结果共有2种。

【点评】这类问题解决的策略是：先用枚举法、列表法或树状图法表示出所有可能出现的结果，然后找出欲求事件的结果数目，最后用概率公式求出概率。两例的区别在于，例3的“从中任意拿出两个”暗示着取到的粽子“不放回”，另外为了保证事件的等可能性，两个肉馅粽子分别记为肉馅1和肉馅2。

考点3 用频率估计概率

例4（2018·内蒙古呼和浩特）某学习小组做“用频率估计概率”的试验时，统计了某一结果出现的频率，绘制了如下折线统计图，则符合这一结果的试验最有可能的是（ ）。

A.袋中装有大小和质地都相同的3个红球和2个黄球，从中随机取一个，取到红球

B.掷一枚质地均匀的正六面体骰子，向上的面的点数是偶数

C.先后两次掷一枚质地均匀的硬币，两次都出现反面

D.先后两次掷一枚质地均匀的正六面体骰子，两次向上的面的点数之和是7或超过9

【解析】A选项中事件发生的概率为：0.6；B选项中事件发生的概率为：0.5；C选项中事件发生的概率为：0.25；D选项中事件发生的概率为折线统计图中试验的频率与D选项中事件发生的概率最接近。

答案：D。

【点评】此题考查利用频率估计概率，大量反复试验下频率稳定值即概率。用到的知识点为：频率=所求情况数与总情况数之比。

考点4 概率与面积

例5（2018·黑龙江绥化）如下图，一块飞镖游戏板由大小相等的小正方形格子构成。向游戏板随机投掷一枚飞镖，击中黑色区域的概率是________。

【解析】击中黑色区域的概率等于阴影面积与大正方形面积之比，即

【点评】此题考查几何概率计算公式以及其简单应用，注意，在等可能条件下，面积之比=几何概率。

考点5 概率与代数、几何等知识的综合运用

例6（2018·江苏扬州）4张相同的卡片分别写着数字-1、-3、4、6，将卡片的背面朝上，并洗匀。

（1）从中任意抽取1张，抽到的数字是奇数的概率是_______。

（2）从中任意抽取1张，并将所取卡片上的数字记作一次函数y=kx+b中的k；再从余下的卡片中任意抽取1张，并将所取卡片上的数字记作一次函数y=kx+b中的b。利用画树状图或列表的方法，求这个一次函数的图像经过第一、二、四象限的概率。

【解析】（1）从4张背面相同的卡片中任意抽取1张，有4种可能，分别是写有数字-1、-3、4、6的卡片，其中数字是奇数的卡片有-1和-3，∴抽到的数字是奇数的概率是

（2）正确画树状图或列表是解决问题的关键，注意本题是“不放回”，另外当k＜0，b＞0时，一次函数y=kx+b的图像经过第一、二、四象限。

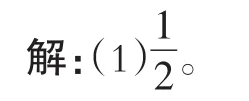
（2）根据题意列表得：

当k＜0，b＞0时，一次函数y=kx+b的图像经过第一、二、四象限。

由表格知：一共有12种可能，其中k＜0，b＞0的情况有4种，

本题也可以画树状图解决，树状图略。

【点评】本题既考查列表法与树状图法求概率，同时又考查了一次函数的性质。首先要画树状图展示所有12种等可能的结果数，然后利用一次函数的性质，找出k＜0，b＞0的结果数，最后根据概率公式求解。