纯电动客车用高速永磁轮边电机损耗分析方法研究

张洪兵，杨思雨，康 娟，丁计飞，秦亚坤

(1河南省财政厅机关服务中心,郑州 450008；2郑州市宇通客车股份有限公司,郑州 450061)

0 引 言

轮边驱动系统具有车内空间利用率高，平顺性与舒适性高的特点，是纯电动客车的发展趋势之一。随着整车续驶里程与可靠性需求的不断提高，对轮边驱动电机的效率与温升等特性提出了更高的要求。电机的损耗直接影响效率与温升，在电机设计时对影响电机损耗的主要因素进行分析，能够为降低电机损耗，提高电机效率，改善电机温升提供依据。高速永磁轮边电机运行时负载与转速非周期变化[1-2]，通过传统方法难以精确计算全工况点的电机损耗[3-4]。因此，需要对电机不同类型损耗进行分离，对全工况范围内损耗的变化趋势进行分析。

本文以一台40kW纯电动客车用高速永磁轮边电机为基础，通过电磁有限元模型对电机铜耗以及齿部、轭部、转子铁耗进行分析，建立考虑非正弦电流激励的电磁损耗模型。对无磁体转子与正常转子电机分别进行空载测试，分离空载铁耗与机械损耗，通过负载损耗测试分离杂散损耗，完成全工况点轮边电机损耗计算模型。最后，将该模型应用于同平台60kW轮边驱动电机的设计中，通过实验验证损耗分析方法的有效性。

1 电机损耗分析基础

永磁驱动电机损耗主要包括：定子铜耗PCu；铁耗PFe；杂散损耗Ps；机械损耗Pfw。

1.1 定子铜耗PCu

非正弦电流激励下，铜耗计算为

PCu=3∑I1k2R1

(1)

式中，I1k为定子相电流各次谐波有效值；R1为定子相电阻。

1.2 铁耗PFe

将总铁耗PFe分解为齿部铁耗PFet、轭部铁耗PFey以及转子铁耗PFer，考虑非正弦激励影响，建立计算模型：

PFei=fFei(n,α,THD)·PFei0

(2)

式中，PFei0为各空载转速点铁耗(i=t、y、r，t表示定子齿部，y表示定子轭部，r表示转子)；fFei为各部分负载铁耗与空载铁耗比例系数；n为电机转速；α为负载率；THD为电流激励谐波系数。

1.3 机械损耗Pfw

机械损耗与电机转速n相关，即

Pfw=ffw(n)

(3)

通过对无磁体转子电机进行空载损耗测试，分离机械损耗并进行建模。

1.4 杂散损耗Ps

杂散损耗可以等效为电机转速与负载功率的函数[5-7]，即

Ps=fs(n,P2)

(4)

在本文中，通过实验测试的总损耗分离出PCu、PFe、Pfw后的剩余损耗均认为是杂散损耗，基于实验结果确定fs并建立等效模型。

2 电磁损耗的确定

通过电磁有限元仿真模型，计算不同转速下电机空载铁耗，得到各部分空载铁耗与转速的关系。进而对正弦激励下负载时定子电流与各部分铁耗进行计算，对电机不同负载下的铁耗进行建模。最后考虑非正弦电流激励的影响，确定各部分铁耗谐波系数，完善铁耗模型。

2.1 电机参数与仿真模型

本文所分析的驱动电机为8极48槽永磁同步电机，定子槽型为梨形槽，转子为内置V字型结构，电机参数如表1所示。并建立如图1所示的单元电机有限元模型进行电磁损耗计算。

表1 电机主要参数

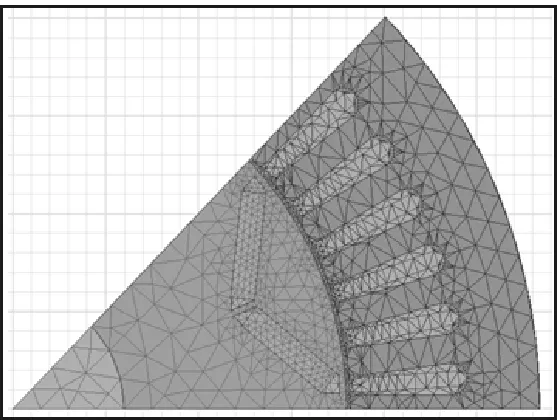
图1 2D电磁仿真模型

2.2 空载铁耗计算

通过对500～7500r/min转速下定子绕组开路时的定子齿部、定子轭部以及转子铁耗分别进行计算，得到不同转速下空载磁场所产生的铁耗。计算结果如图2所示。

图2 空载铁耗计算结果

从图2中的计算结果可以看出，由于电机空载磁场仅由转子磁钢产生，该磁场与转子同步旋转，仅通过齿槽效应使转子磁场产生交变，因此转子铁耗在总空载铁耗中占比较小。随着转速的提高，各部分铁耗变化规律也不同，定子齿部磁密较高，由于铁心饱和效应，齿部磁场谐波含量高于轭部，因此定子齿部铁耗随转速的提高增加速度高于定子轭部。根据图2的计算结果拟合得到各部分空载铁耗与电机转速的关系:

(5)

2.3 正弦激励下负载电磁损耗计算

对转速为500～7500r/min正弦激励额定与峰值工况点的电磁损耗进行计算。电机采用最大转矩电流比控制，定子电流为

(6)

式中，Tem为电机电磁转矩；id、iq分别为电机d、q轴电流；ω为电机电角频率；Ld、Lq分别为电机d、q轴电感；ψf为转子磁链；ulim为极限电压。

根据式(6)确定电机各工况点的定子电流，结合式(1)确定电机铜耗。在有限元模型中对定子绕组施加正弦电流激励，得到各工况点的铁耗计算结果如图3所示。

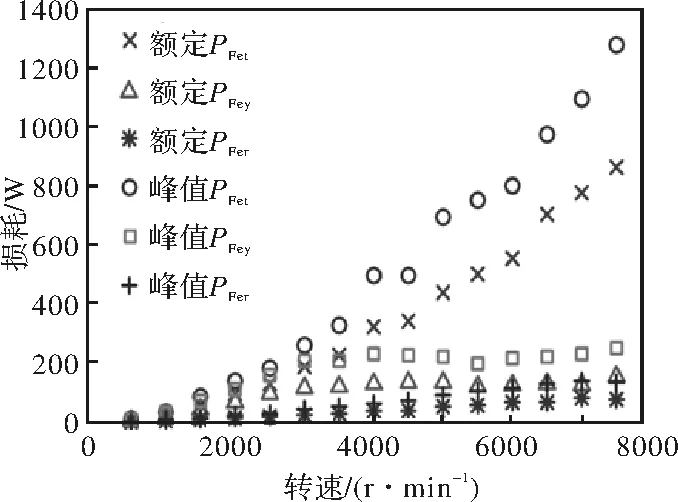
图3 额定与峰值负载下铁耗计算结果

从图3的计算结果可以看出，随着转速的增加，电机齿部铁耗呈现递增趋势。轭部铁耗在电机额定转速以下时有所增加，而在额定转速以上时随转速增加变化不明显。说明电机高速弱磁电流对轭部铁耗的影响高于齿部铁耗，通过分析可知，由于定子电流的弱磁作用，电机轭部磁场相比于定子开路时减小。由于定子绕组磁场在转子铁心中产生交变，因此转子铁耗显著增加。各部分负载铁耗可表示为

(7)

式中，Kt1、Ky1、Kr1为额定负载损耗系数，反映额定负载时各部分铁耗相对空载铁耗的增量；负载率函数ft(α)，fy(α)，fr(α)反映负载率的影响，在α=1时ft(α)，fy(α)，fr(α)均为1；Kw(n)为弱磁系数，反映定子电流弱磁效应对于轭部铁耗的影响，在低于弱磁转速时无弱磁效应。

根据轭部铁耗的计算结果拟合得到

(8)

式中，A1=-0.003738，B1=0.624。

根据额定工况下铁耗与空载铁耗计算结果可以得出，Kt1=2.07，Ky1=1.69，Kr1=4.79。

驱动电机在峰值工作点时各部分损耗相对于额定负载时均有所增加，根据峰值负载时各项铁耗的计算结果，在各部分负载铁耗中考虑负载率的影响，可以得到ft(α)=α0.747，fy(α)=α1.188，fr(α)=α0.614。

2.4 非正弦激励下负载电磁损耗计算

为研究非正弦电流激励对电机铁耗的影响。采用图4所示THD=5.23%的实测定子电流为激励源，进行额定工况负载损耗分析。通过各次谐波分解依据式(1)进行计算。

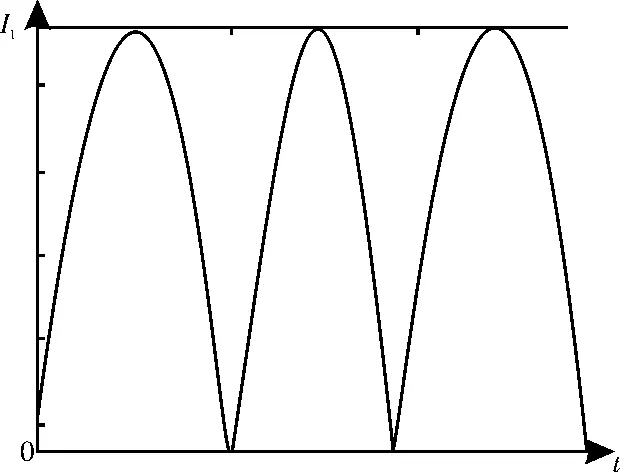
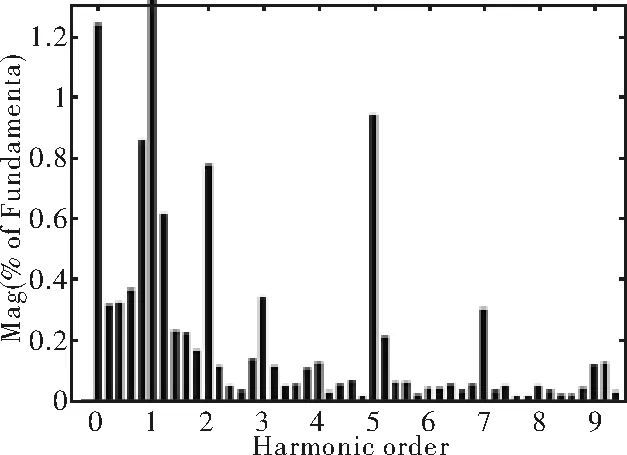
图4 实测电流波形与谐波分布

电机转速为2500r/min、5000r/min与7500r/min时正弦与非正弦激励下电机铁耗如表2所示。

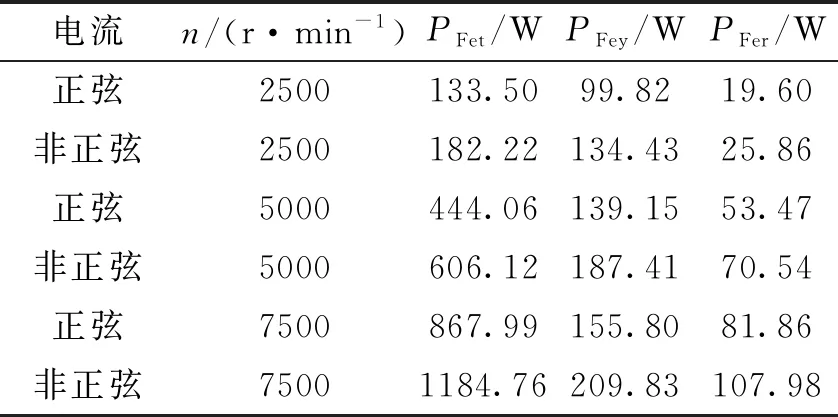
表2 非正弦激励时额定负载铁耗计算结果

从表2的计算结果可以看出，定子电流谐波对于铁耗有显著影响，由于谐波磁场的频率高于基波频率，电流谐波会在铁心中会产生明显的涡流与磁滞损耗。考虑非正弦激励时，各部分铁耗为

(9)

式中，QtTHD、QyTHD、QrTHD为各部分铁耗谐波系数。根据表5的计算结果可得，在THD=5.23%时，QtTHD=1.35，QyTHD=1.63，QrTHD=1.76。

通过电磁损耗有限元计算，确定全工况点电磁损耗基本模型。由于加工工艺会对硅钢片铁耗产生影响，需要通过实验对电磁损耗模型进行修正。

3 机械与杂散损耗分析与建模

通过电机空载测试与无磁体转子电机空载测试将空载铁耗与机械损耗进行分离，建立机械损耗模型，并对依据实验结果对铁耗模型进行修正。进而通过负载测试分离并完善杂散损耗模型。实现全工况点电机损耗分离计算模型的建立。

3.1 空载铁耗与机械损耗分离实验

实验测试中采用主动式测功机测试系统进行空载和负载实验，在测功机和被测电机测试过程中通过数据采集系统和功率分析仪记录测试的各项数据。测试系统如图5所示。

图5 损耗分离实验测试系统

空载损耗测试的目的是分离铁耗与机械损耗，为此，需要进行以下两步实验：

(1)测功机拖动待测电机，测得不同转速下输出的功率，即为待测电机在该转速下的空载总损耗。

(2)将待测电机转子更换为尺寸、重量以及表面粗糙度均相同的无磁体转子，使用测功机拖动待测电机，测得不同转速下测功机输出的功率，即为待测电机在该转速下的机械损耗。

通过以上实验可以计算出机械损耗以及空载铁耗，结果如图6所示。

图6 电机空载损耗实验分离结果

根据机械损耗测试结果，可以得到机械损耗与转速关系为

Pfw=0.000267n1.561

(10)

对图6中的实测空载铁耗与仿真模型计算空载铁耗进行对比，可以看出两者趋势基本一致，通过将各转速下PFe0实测值与PFe0计算值的比值进行平均，得到修正系数KFe=1.12，结合实验结果对式(9)的铁耗模型进行修正，得到各工况点铁耗

PFe=KFe(PFet+PFey+PFer)

(11)

3.2 杂散损耗分离与建模

负载实验测试的目的是进一步对杂散损耗以及电机铜耗进行分离。具体实验与分离计算步骤如下：

(1)测试电机全工作范围内损耗值。

(2)根据图6的结果分离机械损耗。

(3)根据式(11)计算各工况点铁耗。

(4)根据电流实测结果，计算各工况点铜耗。

(5)结合各项损耗实测值分离出杂散损耗。杂散损耗分离结果如图7所示。

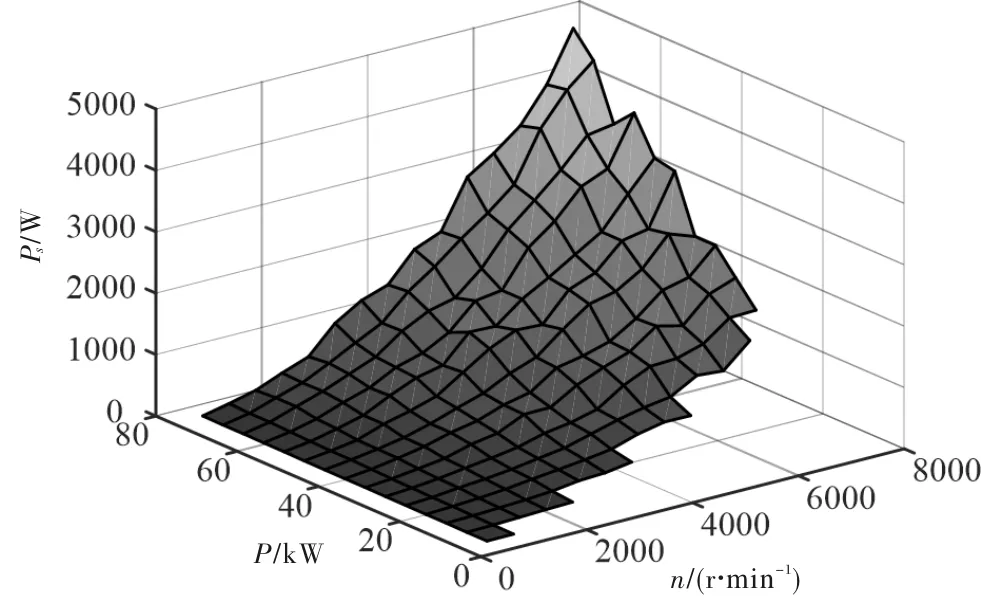
图7 杂散损耗分离结果

根据图7的计算结果，可以看出，在同样输出功率下，杂散损耗随转速增加趋势近似于线性；在相同转速下，随着输出功率的增加，杂散损耗呈指数型增长。因此可以认为杂散损耗主要与转速以及输出功率相关，如:

(12)

式中，n为电机转速；P2为电机输出功率；Ks为杂散损耗系数，根据图7所示的杂散分离结果，拟合参数得到Ks=1.228*10-3；x=1.198；y=1.824。

通过对电机的各项损耗进行仿真计算以及损耗分离实验测试的结果，完成了对电机各项损耗的分离计算模型，实现对轮边驱动电机全工况范围内的各项损耗进行计算。

4 损耗分析方法验证

本文所分析的电机各项损耗中，电机铜耗由定子电流、电阻确定；在同样冲片平台下，铁耗、机械损耗以及杂散损耗随电机转速、负载率等参数的变化趋势基本一致，本文认为其与电机铁心叠高成正比。通过实验验证本文提出的损耗分析方法的准确性。

4.1 电机基本参数

基于相同冲片平台，新设计一台额定功率60kW永磁驱动电机，电机基本参数如表3所示，样机测试如图8所示。

表3 60kW电机主要参数

图8 样机测试照片

4.2 实验验证与分析

应用本文所提出的损耗分离计算方法，对各工况点的各项损耗进行计算，得到由模型计算出的效率map如图9(a)所示。对电机进行效率测试，得到各工况点的效率map如图9(b)所示。最高效率与高效区对比如表4所示。

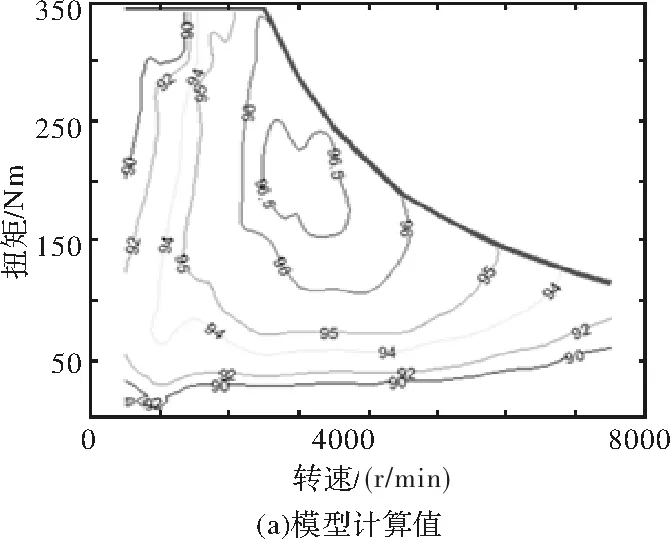
图9 电机效率map

参数计算值实测值最高效率96.56%96.88%80%效率以上高效区84.92%86.67%85%效率以上高效区80.64%81.05%

通过表4的对比可以看出，电机高效区计算结果与实验结果吻合度高。实验表明本文所建立的模型能够有效对同平台轮边电机的损耗与效率进行分析，为永磁轮边电机的设计提供参考。

5 结 论

本文首先针对一台40kW纯电动客车轮边电机进行电磁损耗的有限元计算，考虑非正弦激励影响，建立电磁损耗计算模型。利用实验分离机械与杂散损耗，并建立全工况下损耗计算模型。同平台60kW样机的测试结果表明，所建立的损耗模型能够准确计算电机损耗，有效支撑电动汽车平台化驱动电机的设计。