基于Elman神经网络观测器的永磁同步电机无传感器控制

孙凯翔 ,胡兆稳, 丁曙光,王 伟, 彭 群 ,阚超豪

(1.合肥工业大学 机械工程学院,合肥 230000；2.合肥工业大学 电气与自动化工程学院,合肥 230000)

0 引 言

永磁同步电机(PMSM)以其结构紧凑、转矩惯量比高、功率密度高、效率高等优点，在理论研究和应用中都得到了广泛的关注[1-2]。在传统的矢量控制系统中，通常采用传感器来获取电机的转速和位置信息。然而，在实际应用中，传感器不仅安装和维护困难，而且价格昂贵。另外也降低了系统的可靠性，限制了PMSM在恶劣环境中的应用[3]。因此，对PMSM无传感器控制方法的研究具有重要的意义。

目前，国内外学者提出了众多方法来估计电机转子的速度和位置。文献[4]提出了一种能满足低速和高速运行的变结构定子磁链观测器。在低速状态下，该方法比传统的磁链估计方法具有更高的精度。然而，转速估计值的波动较大，磁链估计误差较大。在高速状态下，转速估计误差增大，暂态收敛速度较慢。文献[5]提出了一种基于参数优化理论的PMSM模型参考自适应系统，该方法具有结构简单、响应速度快、精度高等优点。然而，该方法的精度过于依赖于精确的电机参数。文献[6]采用扩展卡尔曼滤波算法估计PMSM的转速和位置。该方法可用于噪声环境下的状态、参数和未知扰动的估计。然而，该方法计算量大，对电机参数有依赖，测量噪声和系统噪声的统计特性在实际应用中尚不明确。

近年来，随着人工神经网络(ANN)的发展，其突出的自学习和自适应能力越发引起人们的关注。对于数学定义不明确的系统，ANN可以实现结构化和非结构化的鲁棒逼近。并且理论上，它可以以任意的精度逼近任意的连续函数[7]。所有这些特征表明了ANN在电机驱动系统中的应用潜力[8-9]，包括PMSM的无传感器控制。在文献[10]中，采用3个对角递归神经网络(DRNN)来实现PMSM的无位置传感器控制。其中DRNN电流观测器和速度观测器都具有离线训练和在线训练过程，然而DRNN位置观测器只有离线训练过程。当电机参数发生变化时，无法保证DRNN位置观测器的位置估计精度，从而影响其他观测器的估计精度。文献[11]提出了一种基于递归神经网络的状态观测器来估计电机速度，并利用李雅普诺夫理论设计了在线训练律。然而，该方法在暂态过程中转速误差和位置误差较大，收敛速度较慢，且系统对电机参数扰动的鲁棒性没有得到验证。文献[12]选择直轴电压方程作为PMSM无位置传感器控制的估计模型，并采用递归Elman神经网络(ENN)估计转速。然而，转速的估计精度和收敛速度还有待进一步提高，同时对电机参数扰动的鲁棒性研究也不充分。

为了提高精度和误差收敛速度，提出了一种基于ENN的转速自适应观测器。研究了系统对影响PMSM无传感器控制性能的各种因素的鲁棒性，并利用Lyapunov稳定性理论分析了ENN训练过程的稳定性。ENN作为一种递归神经网络，具有较强的记忆历史数据的能力，因此可以有效地检测和识别时变模型[13]。根据ENN的训练特性和交轴电压方程，计算出实际电角速度与估计电角速度之间的误差，从而支持ENN的在线训练。采用Levenberg-Marqudt算法(LM算法)作为训练算法。该算法具有全局搜索和局部搜索特性，可以加快权值阈值的更新，使权值阈值收敛更加精确[14]。

1 PMSM建模

d-q坐标系下表贴式PMSM数学模型及动力学方程如下：

(1)

(2)

(3)

(4)

(5)

式中,ud,uq为d-q轴电压；R为电阻;id,iq为d-q轴电流；ψ为永磁体磁链；Ld,Lq为d-q轴电感；p为极对数；Te为电磁转矩；B为阻尼系数；TL为负载转矩；wm为机械角速度；J为转动惯量；we为电角速度；θe为电角度。

2 ENN及LM算法

2.1 Elamn神经网络结构

如图1所示，ENN包括输入层、隐藏层、递归层和输出层。与传统的前馈神经网络相比，ENN的特点是：隐层神经元具有递归层反馈，反馈连接之间存在一个采样周期延迟。由于隐藏层的反馈，ENN对历史数据很敏感，即ENN具有记忆功能。ENN的这一特性对动态系统的建模具有重要意义。

图1 ENN结构

第j个隐层神经元的输入如下：

(6)

式中，max(j) =max(J)。

第j个隐层神经元的输出为

vj(k)=f(Uj(k))

(7)

式中,f(·)为激活函数，通常为tansig函数：

(8)

第m个隐层神经元的输出为

(9)

其中,上标I,H,O分别代表输入层、隐藏层、输出层；wI,wHwO, 分别代表输入层与隐藏层、递归层与隐藏层、隐藏层与输出层的连接权值；Ii(k)为第i个输入层神经元在k时刻的输入；bH与bO分别代表隐藏层与输出层的阈值。

2.2 Levenberg-Marquardt算法

神经网络常用的误差反向传播算法(BP算法)及其改进算法遵循梯度下降原理。权值阈值沿误差梯度相反的方向移动，减小性能函数，直到性能函数达到目标值。基于BP算法的神经网络理论上能够逼近任意非线性连续映射，但存在一些已知的缺陷。BP算法的缺点主要是收敛速度慢，容易陷入局部极小值，数值稳定性差，学习速度、动量系数难以调整。这些缺点降低了BP算法于在线训练和控制中的表现。

LM算法是高斯-牛顿算法和梯度下降算法的结合，兼具高斯-牛顿算法的局部收敛性和梯度下降算法的全局收敛性。能够通过自适应调整阻尼因子，加快收敛速度，提高收敛精度，取得更好的性能[15]。

设神经网络权值阈值所组成的向量为

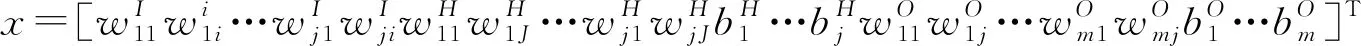
(10)

式中,上标T代表向量的转置。

第m个输出层神经元的期望输出与估计输出的误差为

em=dm-ym

(11)

神经网络性能函数为

(12)

权值阈值的变化为Δx，对于牛顿法有：

Δx=-[2V(x)]-1V(x)

(13)

(14)

式中,J(x)为雅克比矩阵，S(x)为误差函数：

(15)

式中,下标n为向量x的维度。

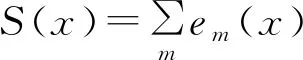
(16)

S(x)难以计算，LM算法将其忽略。

对于高斯-牛顿法为

Δx=-[JT(x)J(x)]-1JT(x)e(x)

(17)

LM算法是高斯-牛顿法的改进，即：

Δx=-[JT(x)J(x)+μI]-1JT(x)e(x)

(18)

式中,阻尼因子μ>0，I为单位矩阵。

从式(18)中可以知道，当μ很大时，LM算法近似于梯度下降法。当μ=0时，则为高斯-牛顿法。因为利用二阶导数信息，LM算法比梯度下降法快得多。而且JT(x)J(x) +μI是正定的，所以式(18)的解总是存在的，而对于高斯-牛顿法，JT(x)J(x)是否满秩还是一个潜在的问题。从这个意义上说，LM算法优于高斯-牛顿法。

LM算法流程如下：

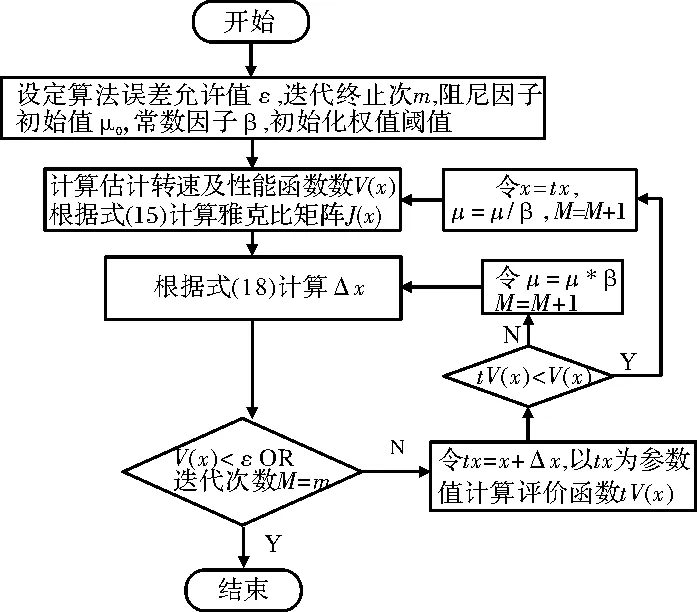
图2 LM算法流程

2.3 离线训练

设Ts为采样周期，将式(4)代入式(3)并离散化可以得到：

(19)

选择式(19)作为ENN速度观测器的估计模型。时刻k设为当前时刻，时刻k-1设为上一时刻。通常，负载转矩TL变化不频繁，将TL视为常数。离线训练数据来自于提前采集。离线训练开始于权值阈值的初始化，输入数据为we(k-1)和iq(k-1) ，期望输出为we(k)。每次训练，根据ENN输出与期望输出得到性能函数，然后根据训练法则调整ENN的权值阈值。当性能函数满足训练目标或达到最大训练次数，离线训练结束。

2.4 在线训练

对于ENN，在线训练过程与离线训练相似。然而，在PMSM无传感器控制中，转速和位置无法直接获得。因此，只能通过其他方法来获得转速信息。结合ENN学习特性将电压方程中的转速信息提取出来用于ENN在线学习。

将式(2)离散化，可以得到式(20)。其中所包含的物理量为实际值。

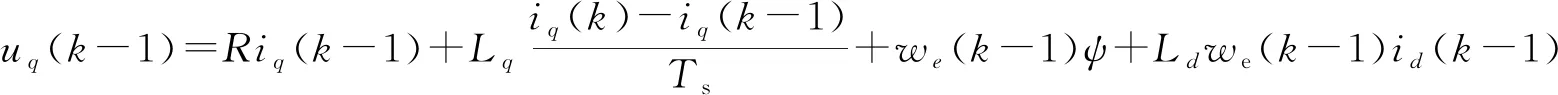
(20)

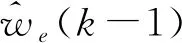
(21)

式(20)减去式(21)得到：

(22)

因此，k-1时刻的电角速度估计误差为

(23)

在k时刻得到k-1时刻的电角速度估计误差，将Δwe(k-1)用作ENN学习对象从而实现权值阈值调整。

如果选择式(1)构造电角速度估计误差，可以得到：

在电机运行过程中，当iq=0时，无法计算，因此不是理想选择。

(24)

(25)

2.5 训练过程稳定性分析

为了证明ENN训练过程的稳定性，定义如下李雅普诺夫函数：

(26)

式中,‖·‖为欧式范数，阻尼因子μ>0。

根据式(10)～式(15)，可以得到如下方程：

(27)

(28)

(29)

假设：状态x*是性能函数V(x)的平衡状态或最小值状态。

根据人工神经网络通用逼近理论[7]，ANN能够以任意精度逼近任意非线性函数。因此，当ENN经过足够的训练后，在平衡状态ENN的输出与实际输出之间的误差可以忽略。

在平衡状态可以得到以下方程：

V(x*)=0

(30)

(31)

定理：在平衡状态x*某邻域内，标量函数L(x)具有连续一阶偏导数，且满足

L(x)为正定的标量函数；

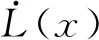
则平衡状态x*是一致渐进稳定的。

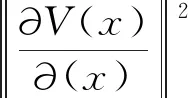
显然，L(x)是正定的。

将式(26)对时间微分，可以得到：

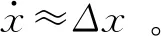
将式(18)代入式(33)，可以得到：

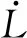
根据Lyapunov稳定性理论，ENN训练过程的稳定性得到证明。

3 仿真结果

离线训练后，通过多种因素验证ENN观测器的性能，例如：机械参数扰动、负载扰动、电磁参数扰动。PMSM参数如表一所示，控制系统框图如图3所示。

表1 永磁同步电机参数

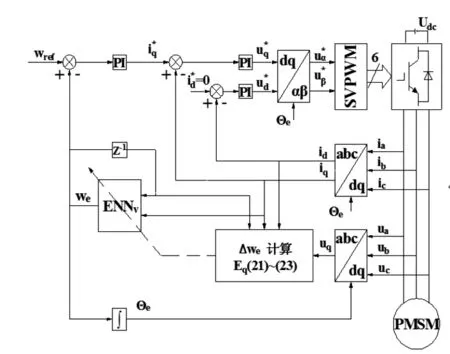
图3 PMSM控制系统框图

为了验证观测器对负载转矩扰动的鲁棒性，设定初始时TL=0，0.2 s时负载转矩变化为TL=3 Nm。从图4(a)可以看出无论在暂态还是稳态，ENN观测器的估计转速与电机实际转速非常接近。在0.2 s时，负载转矩发生变化，引起电机转速的变化。ENN观测器通过在线学习实时调整权值阈值，从而准确跟踪变化的转速。从图4(a)中0.2535～0.2550 s，估计转速在实际转速附近波动，且波动的范围很小。

图4 负载扰动时转速及位置跟踪

如图4(b)所示，在暂态时，观测器估计转速与实际转速最大误差达4 r/min。0.15～0.25 s稳态阶段，负载转矩变化前观测器估计误差非常小，在 0.1 r/min范围内波动。负载转矩变化后，观测器估计误差在 0.4 r/min范围内波动。因此，观测器能够准确跟踪电机实际转速。

如图4(c)与图4(d)所示，ENN观测器估计转速经过积分后得到的估计位置能够准确跟踪转子实际位置，且误差非常小。因此，转子位置能够被准确跟踪，ENN观测器对负载转矩扰动具有很强的鲁棒性。

为了验证ENN观测器对转动惯量扰动的鲁棒性，在0.004 s令转动惯量增大5倍。如图5所示，转动惯量的变化引起电机转速的变化。ENN观测器能够有效学习这种变化，逼近变化后的动力学方程(19)，从而准确跟踪变化的电机转速与位置。从相应的曲线可以看出，观测器的跟踪是准确有效的，ENN观测器对转动惯量的扰动具有很强的鲁棒性。

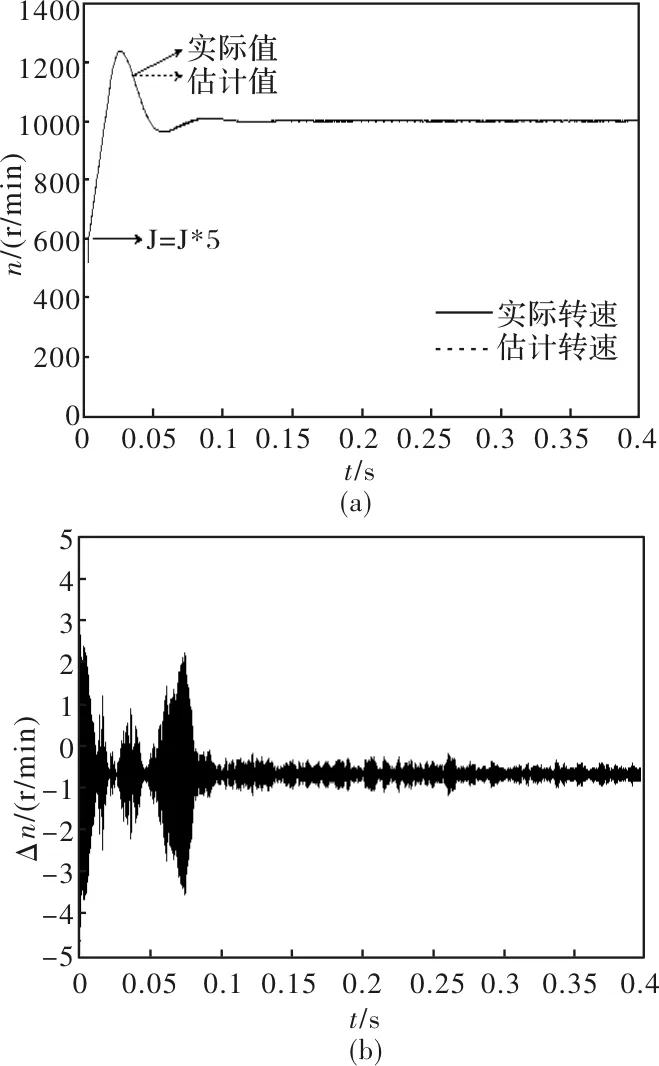
式(19)被选择为ENN转速观测器的估计模型，当其中的机械参数或负载转矩发生后，ENN能够通过自学习逼近变化后的动力学方程，从而能够始终准确的估计电机转速，对机械参数，负载转矩具有很强的鲁棒性。

以上的研究是基于电磁参数准确的前提下，然而在电机运行过程中，电磁参数会因为受到温度变化，磁饱和，负载扰动的影响而发生变化。为了验证ENN观测器对电磁参数的鲁棒性，程序中式(21)、式(22)、式(23)所包含的电磁参数如表1设置。电机的实际电阻值、电感值、磁链值分别增大10%、3%、10%。

如图6所示，在电阻值有10%误差前提下，观测器仍然能够准确跟踪电机转速。在暂态阶段，转速及位置的估计误差相对较大，然后转速估计误差迅速收敛并在±3r/min范围内波动，位置估计误差收敛到4*10-3rad。结果表明在电阻值不准确的情况下ENN观测器仍有较好的性能。

图7 电感不准确时转速及位置跟踪

如图7所示，在电感值有3%误差前提下，ENN观测器的估计转速与实际转速之间有较大的误差，对电感扰动比较敏感。但是由于ENN观测器的估计转速围绕实际转速比较均匀的上下波动，电机实际转速能够稳定上升至额定转速，且位置估计误差较小。

图8 磁链不准确时转速及位置跟踪

如图8所示，在磁链值有10%误差前提下，ENN观测器的转速估计仍然准确。暂态时，转速估计误差相对较大，然后迅速收敛并在±0.5r/min范围内波动。位置估计误差收敛至0.107rad。

4 结 语

为了解决PMSM无传感控制问题，本文提出了一种基于ENN观测器的控制方法，并制定了有效的神经网络在线学习策略。另外，通过Lyapunov稳定性理论证明了神经网络权值阈值的平衡状态是一致渐进稳的。仿真结果证明，无论在暂态还是稳态，ENN观测器能够准确跟踪电机转速及位置；对于机械参数扰动、负载扰动具有很强的鲁棒性；对于电磁参数在一定范围内的扰动具有较强的鲁棒性。因此，所提出的控制方法对高性能伺服驱动的发展是有意义的。

然而，当电磁参数扰动较大时，ENN观测器会有一定的估计误差，为了保证高性能伺服驱动所需精度，ENN观测器可以结合适当的电磁参数辨识方法。