基于MRAS的无轴承同步磁阻电机无位移传感器控制

张汉年，段向军，张 涛，鲍安平

(1.南京信息职业技术学院 中认新能源技术学院，南京 210023； 2.淮阴工学院 自动化学院，江苏 淮安 223003)

0 引 言

无轴承同步磁阻电机是一种集成转子悬浮支撑与旋转功能于一体的新型特种磁悬浮电机[1]，它将产生转子悬浮力的悬浮绕组叠放于普通同步磁阻电机电枢铁心中，通过悬浮绕组和转矩绕组电流形成两种不同极对数的旋转磁场，两种磁场相互作用实现转子的高速旋转和稳定悬浮。同其他类型的无轴承交流电机相比，具有凸级转子的无轴承同步磁阻电机以免润滑、控制简单、转子坚固可靠、转速高等优点，在飞轮储能发电、高速精密机床电力驱动、高洁净生物医学工程等领域具有较大的工程应用前景。

为满足无轴承同步磁阻电机高速、高精度悬浮控制的需要，必须对转子径向位置进行闭环控制，通常是在电机内部安装机械式电涡流位移传感器进行转子位移的精确检测，但安装机械位移传感会使电机轴向长度变长、破坏电机固有的机械结构、增大位移信号检测系统的安装和调试难度、影响系统的廉价性，将进一步制约无轴承同步磁阻电机的推广应用。

成本低、可靠性高的无位移传感器技术成为当前无轴承同步磁阻电机领域的研究重点，目前已经提出了多种无位移传感器控制策略。文献[2-3]是基于电机电感参数和精确数学模型，提出了无轴承同步磁阻电机的无位移传感自检测技术，但该方案对参数变化较为敏感，转子位移估算误差较大。文献[3]提出在无轴承同步磁阻电机悬浮绕组和转矩绕组注入高频脉动信号，以提取转子位移信息，但额外注入的高频信号会带来电磁转矩脉动增强、转子悬浮控制精度降低等问题。基于模型参考自适应系统(MRAS)的电机无传感器控制是将实际运行的控制模型作为参考模型，并以此建立可调模型，再设计一个自适应机构去调整参考模型和可调模型的输出误差为零，得到待辨识量。模型参考自适应法目前在交流电机无速度传感器控制和电机参数辨识等领域获得广泛应用[4]，但尚未发现其用于无轴承同步磁阻电机的无位移传感器控制。本文提出了基于模型参考自适应的无轴承同步磁阻电机转子位移估计方法，仿真和实验结果证实了该方案的有效性。

1 模型参考自适应转子位移估计系统

1.1 转子位移MRAS估计原理

无轴承同步磁阻电机在两相同步旋转d、q坐标系中的磁链方程为[5]

(1)

式中，Ψd、Ψq分别为转矩绕组磁链d、q轴分量，Ψx、Ψy分别为悬浮绕组磁链d、q分量，Ld、Lq分别为转矩绕组电感d、q轴分量，Lx、Ly分别为悬浮绕组电感d、q轴分量，x、y分别为两轴方向转子径向位移，K1、K2分别为悬浮力/电流常数d、q轴分量，id、iq分别为转矩绕组电流d、q轴分量，ix、iy分别为悬浮绕组电流d、q轴分量。

无轴承同步磁阻电机在d、q坐标下定子绕组的电压方程可表示为

(2)

式中，ud、uq分别为转矩绕组电压d、q轴分量，ux、uy分别为悬浮绕组电压d、q轴分量，d/dt为微分算子，Rs1、Rs2分别为转矩绕组和悬浮绕组每相电阻，w为转子角速度。

将式(1)代入式(2)，并忽略x、y的二次项，可得无轴承同步磁阻电机定子电流数学模型为

(3)

式中,i=[idiqixiy]T,u=[uduquxuy]T,

由式(3)可看出电机电流模型与转子位移有关，可将其作为电机定子电流参考模型。

依据式(3)，进一步设计电机定子电流观测器的并联可调模型为

(4)

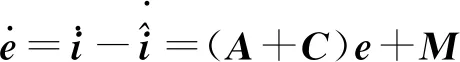
(5)

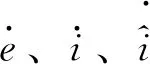
(6)

式中，Kp1、Ki1分别为转子x轴方向PI调节器比例、积分系数，Kp2、Ki2分别为转子y轴方向PI调节器比例、积分系数，s为拉普拉斯算子，

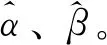
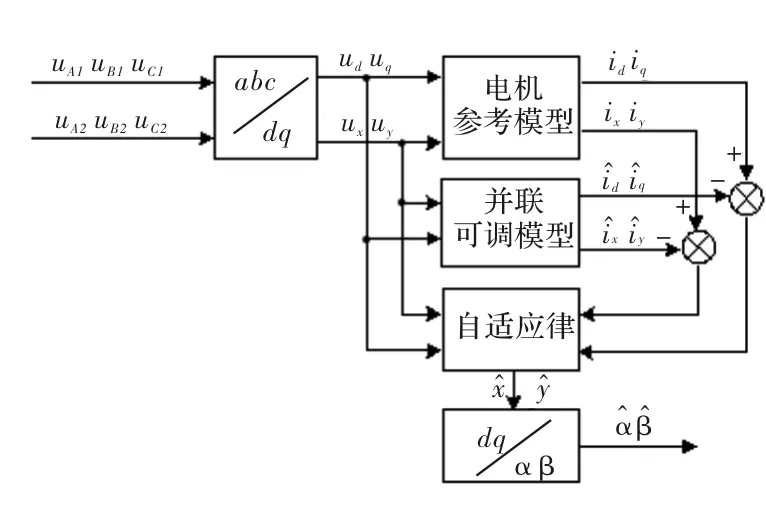
图1 MRAS转子位移估计系统

1.2 基于MRAS的无位移传感器控制系统

无轴承同步磁阻电机转矩子系统与普通同步磁阻电机控制策略相同，此处采用恒定id控制(id=常数，但不为零)。在d、q坐标下，电磁转矩Te的表达式为

(7)

式中，p1为转矩绕组极对数。

α、β静止坐标下电机悬浮力/电流调制模块的数学模型[6]

(8)

式中，Fα、Fβ分别为悬浮力α、β轴分量，iα2、iβ2分别为悬浮绕组电流α、β轴分量，θ为电机转子位置角。

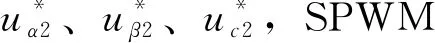
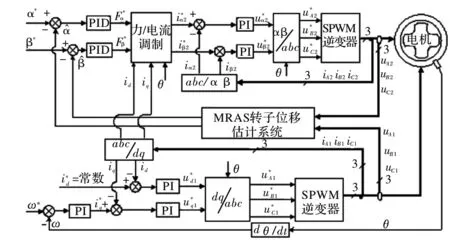
图2 电机无位移传感器控制系统结构

2 仿真实验分析

2.1 仿真研究

为验证模型参考自适应无位移传感器控制方法的有效性，基于图2系统结构建立了仿真模型，进行了仿真研究。电机主要参数如表1所示，仿真结果如图3～图6所示。

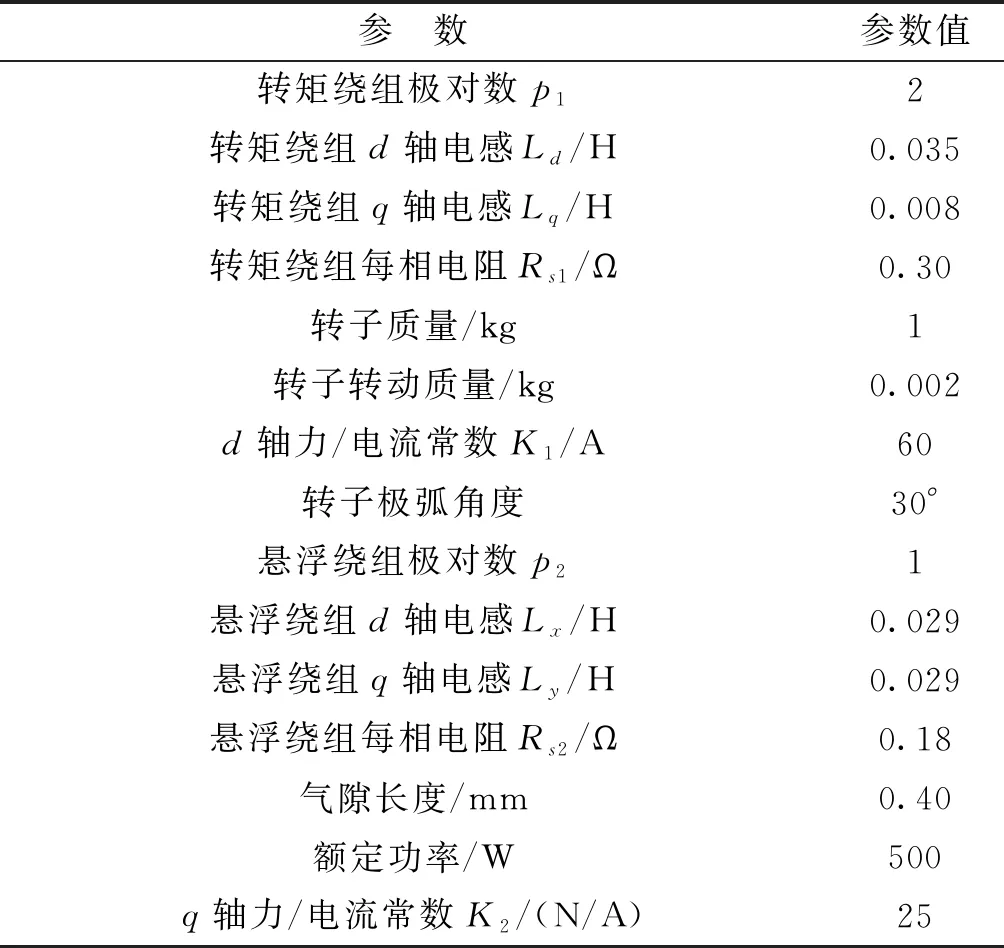
表1 电机参数

图3、图4分别为电机转矩和转速仿真曲线。图3为电机空载起动，0.02 s时突加3 Nm负载。图4为转速初始值设置为1000 r/min，0.2s突变为2000 r/min。由图可知，电机转矩和转速稳态误差小，动、静态调节性能良好。

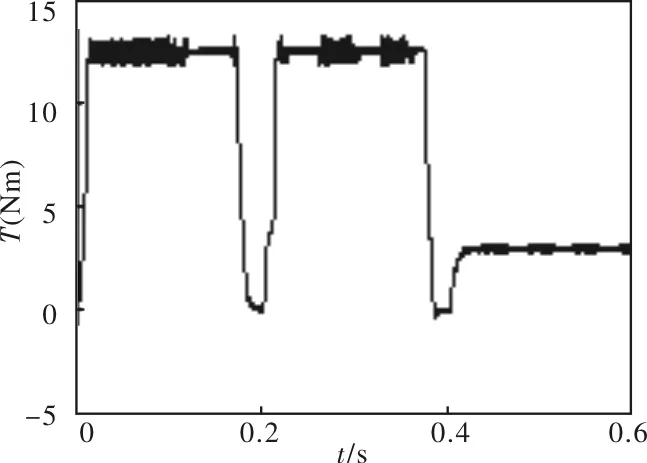
图3 转矩仿真曲线

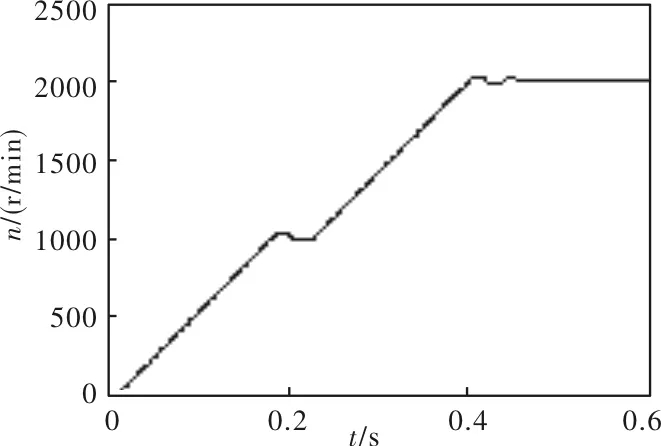
图4 转速仿真曲线

图5、图6分别为α、β轴转子位移在有传感器检测和MRAS位移估计法(无位移传感器)条件下的对比图，此时电机转矩和转速仍按上述给定条件。

图5中α轴初始位移设定为α=-0.10 mm，由对比曲线可以看出，相比有位移传感器，MRAS估计法α轴位移偏差增大、响应速度稍慢，但转子位移脉动范围未超过电机限位轴承气隙0.4mm，转子最终能趋于α=0位置。

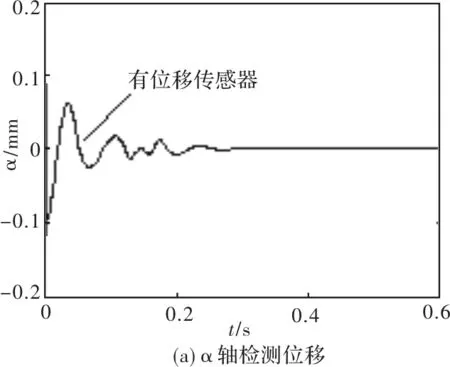
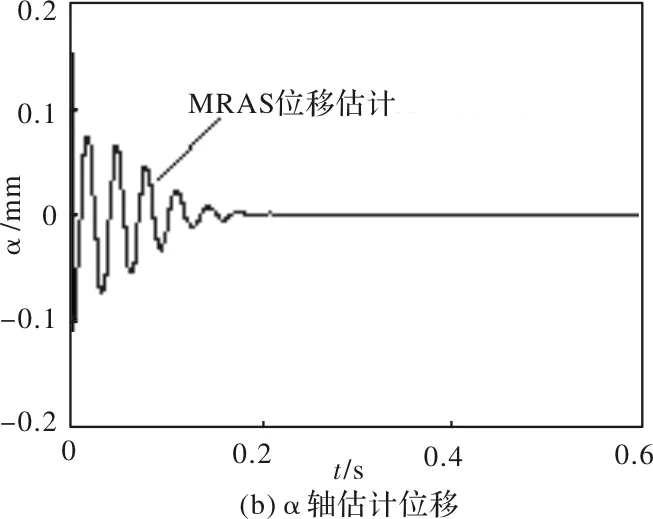
图5 α轴位移仿真曲线

图6中β轴初始位移设定为β=0.10 mm，由对比曲线可看出，采用MRAS估计法比有位移传感器时转子位移振动幅度要大，但没有超出限位轴承气隙长度，经过一段时间的波动后转子最终能收敛于β=0位置。

结合图3～图6可以看出，电机转矩和转速突变过程中，转子径向位移并未受到影响，能实现稳定悬浮运行，表明模型参考自适应无位移传感器系统具有良好的抗干扰能力。

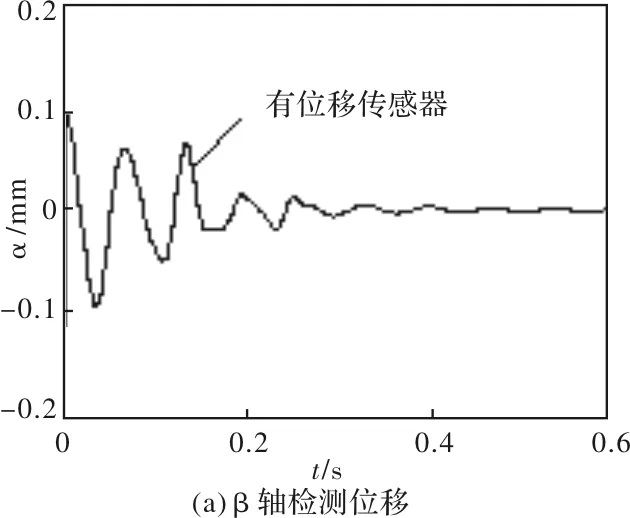
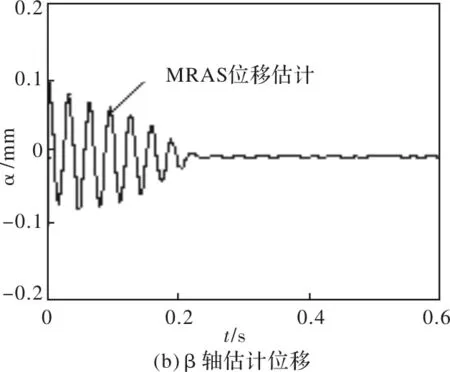
图6 β轴位移仿真曲线

2.2 实验结果

图7为电机在转速1500 r/min稳态运行时α、β轴转子位移曲线。可以看出，MRAS位移估计法与有位移传感器相比，转子径向位移总的跳动幅度稍大。但MRAS法转子位移波动的最大范围不超过145 μm，远小于电机机械辅助限位轴承气隙0.4 mm，转子能够实现平稳悬浮，进一步表明本文所提方法的可行性。

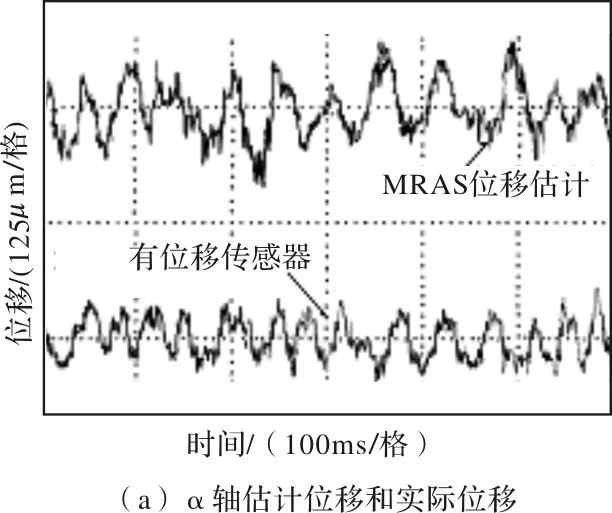
图7 转子估计位移和实际检测位移对比曲线

3 结 语

基于MRAS的无轴承同步磁阻电机无位移传感器控制方法克服了机械位移传感器带来的不利影响，是实现低成本、高可靠性无轴承同步磁阻电机悬浮运行的有效途径。本文对无轴承同步磁阻电机转子位移MRAS估计方法进行了研究，分析了MRAS转子位移辨识原理，建立电机定子电流的参考模型和可调模型，设计出电机无位移传感器整体控制系统。为验证方法的可行性，进行了系统的仿真和实验研究，结果表明模型参考自适应法能够实现转子位移的实时跟踪和准确估计，电机悬浮性能良好，系统具有较好的抗干扰能力。