基于分类型矩阵对象数据的MD fuzzy k-modes聚类算法
2019-06-26李顺勇张苗苗曹付元
李顺勇 张苗苗 曹付元
1(山西大学数学科学学院 太原 030006)2(山西大学计算机与信息技术学院 太原 030006)
聚类算法中最具代表性的是k-means,k-modes,k-prototype算法,其中,k-means[1]主要用于对数值型数据进行聚类.现实中,分类型属性数据也常见.1998年Huang[2]提出了k-modes算法,该算法用简单匹配计算2个对象间的距离,用modes代替means,基于频率来更新类中心.2001年Chaturvedi等人[3]改进了k-modes算法,提出了k-modes-CGC算法,有效地运用非参数方法对分类型数据进行聚类.随后,Huang等人[4]证明了二者的等价性.此外,在初始类中心的选取上,Ying等人[5]考虑将迭代求精法与k-modes算法结合;在相异性度量的选取上,Ng等人[6]和San等人[7]基于属性频率计算相似度,Li等人[8]基于生物特征计算距离.Liang等人[9-14]也基于不同度量提出了多种k-modes的改进算法.
以上种种算法在考虑类别归属时,其隶属度只考虑了0,1这2个值,即只能划分到确定的某一类中,属于硬划分.而数据的不同属性重要度会给部分数据的真实类别归属带来模糊性.粗糙集[15]和模糊集[16]理论的提出为数据在数据集中的位置提供了有利的基础,软划分应运而生.Bezdek提出的fuzzyc-means(FCM)算法[17]是软划分聚类的典例.1999年Huang等人[18]在FCM算法的基础上引进模糊因子、隶属度矩阵等,进一步提出fuzzyk-modes算法.2004年Kim等人[19]用模糊集对类中心的模糊化刻画分类数据中类的不确定性,提出了具有模糊类中心的Fuzzyk-modes算法.2005年Li等人[20]提出了基于特征加权的模糊聚类新算法(novel feature weighted clustering algorithm, NFWFCA).2007年Cai等人[21]结合局部空间和灰度信息,提出了快速通用的聚类算法(fast generalized fuzzyc-means, FGFCM).2016年Zhou等人[22]结合多目标优化算法与模糊中心点聚类,提出一种新颖的多目标模糊聚类算法.总之,k-modes算法对后续众多的拓展算法起到了积极的铺垫作用.
已有的聚类算法普遍使用X={X1,X2,…,Xn}的数据表示模式,X表示由n个对象组成的对象集,Xi=(Xi1,Xi2,…,Xim)表示每个对象由m个属性特征描述,每个属性特征有且仅有唯一的取值.然而实际应用中,对象的每个属性特征可能有不同的取值.例如顾客购物时,可能同时购买多个产品,这就容易产生矩阵对象数据[23].若利用已有的聚类算法处理该类数据,需用先验知识来选取其中一条记录,这会严重损失信息并破坏数据的原始性,且违背了以数据总体来做数据分析的初衷.因此,为了利用多条消费记录发现客户的消费喜好,从而做出更具针对性的推荐[23],有必要研究基于矩阵对象数据的聚类算法.Cao等人[24]首先提出基于集值对象的Set-Valuek-modes (SV-k-modes)算法和fuzzy Set-Valuek-modes(fuzzy SV-k-modes)算法[25].之后,Cao等人又提出基于矩阵对象的k-multi-weighted-modes(k-mw-modes)聚类算法[23].该算法在考虑类别归属的同时,其隶属度也仅仅考虑了0,1这2个值.由于数据集中属性重要度的不同,常常会给部分数据的真实类别归属带来模糊性.本文兼顾模糊集引入模糊因子,提出一种基于矩阵对象数据的模糊聚类算法(matrix-object data fuzzyk-modes, MD fuzzyk-modes).本文的主要贡献有4个方面:
1) 结合模糊集的概念提出了一种更新类中心启发式算法;
2) 提出了基于分类型矩阵对象数据的MD fuzzyk-modes聚类算法;
3) 实验验证了MD fuzzyk-modes算法的有效性;
4) 分析了模糊因子β与隶属度w的关系.
1 回顾fuzzy k-modes算法
设X={X1,X2,…,Xn}是由n个对象、m个属性描述的分类型数据集,则Xi与Xj间的相异性度量定义为
(1)
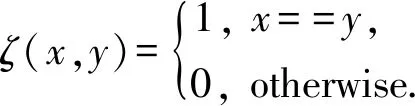
Q是X的类中心,如果Q能最小化
(2)
fuzzyk-modes算法用迭代方式将数据分为k类, 此算法的目的是最小化目标函数:
(3)
其中,W为隶属度矩阵.
2 MD fuzzy k-modes聚类算法
经典的k-type算法[1-2]主要由3部分组成:相异性度量的定义、类中心的表示和类中心的更新过程.本文提出的MD fuzzyk-modes算法也从这3方面考虑.
2.1 矩阵对象间的相异性度量
用简单0-1匹配、属性频率等相异性度量来计算数据间的距离适用于1对1对象数据,而矩阵对象数据每个属性有多于一个的属性值,这些相异性度量对矩阵对象数据有一定的局限性,由于k-mw-modes算法[23]中定义了2个矩阵对象间的相异性度量,本文直接引用此相异性度量.
定义1.相异性度量.给定矩阵对象Xi,Xj,每个对象由m个分类型属性{A1,A2,…,Am}来描述,则Xi与Xj的相异性度量定义为
(4)
其中:
δ(Xis,Xjs)=
(5)
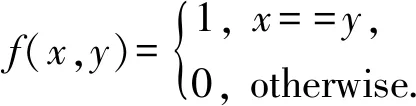
(6)
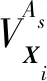
可以验证该相异性度量满足非负性、对称性和三角不等式性,的确是一个距离.
例1.表1是某一矩阵对象数据集的描述,其中X={X1,X2},A={A1,A2},计算X1,X2间的距离.
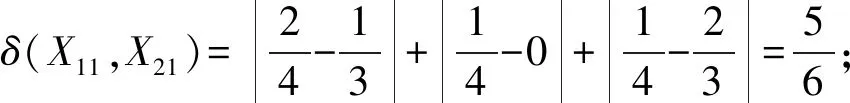

Table 1 A Matrix-Object Data Set表1 某一矩阵对象数据集
2.2 类中心的定义及启发式更新过程
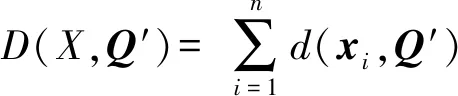
定义2.类中心.如果Ql能使目标函数达到最小:
(7)
则Ql是X的类中心.
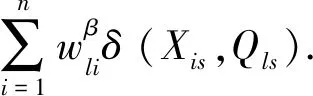
这种全局性更新类中心算法的时间复杂度为O(nmtk×2|V′|),n表示对象数,m表示属性个数,k表示分类个数,t表示迭代次数,|V′|=max{|Vs|,1≤s≤m}.由此可知,全局性更新类中心的算法时间复杂度随着对象个数、属性个数、分类数及迭代次数的增多呈线性增长,属性值的个数呈指数增长.
当矩阵对象数据中属性值个数过多时,全局更新类中心的算法计算量过大,耗时增强,故本文提出了启发式更新类中心算法.首先分析
(8)
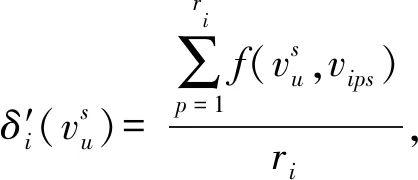


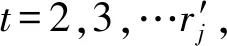
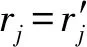

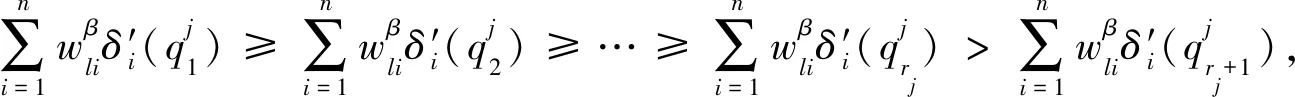
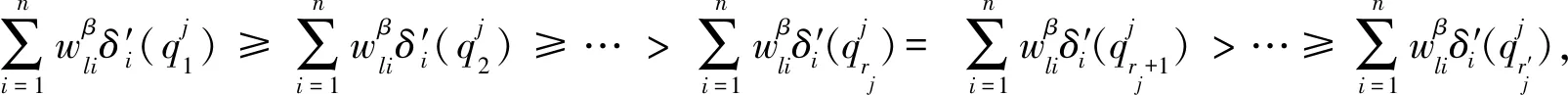
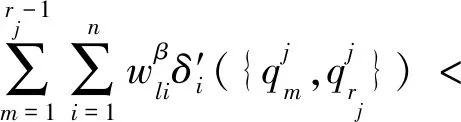
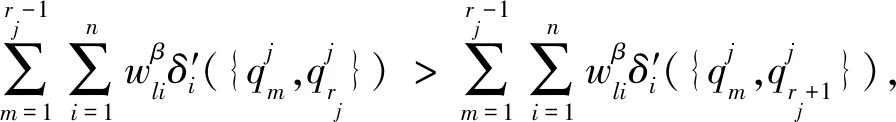
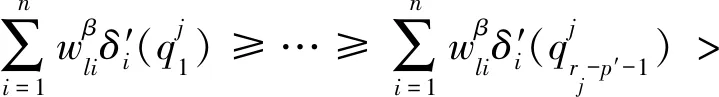
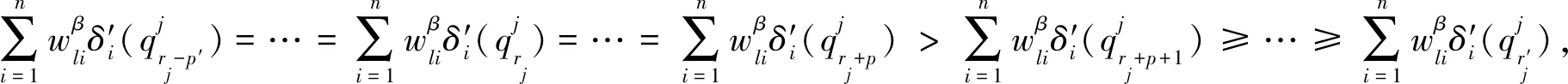
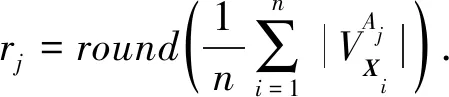
2.3 MD fuzzy k-modes聚类算法
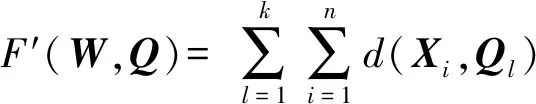
本文在k-mw-modes算法的基础上,引入模糊因子并改进了类中心的表示及更新过程,提出了MD fuzzyk-modes算法.
定义3.最小化目标函数.将一矩阵对象数据集X={X1,X2,…,Xn}划分为k类,则需最小化目标函数:
(9)
且满足:
wli∈[0,1], 1≤l≤k, 1≤i≤n,
(10)
(11)
(12)
其中,Q=(Q1,Q2,…,Qk)中的元素Ql表示第l类的中心,Ql=(Ql1,Ql2,…,Qlm);W=(wli)是一个k×n维的隶属度矩阵,wli=1表示Xi被分到l类.
为使F′(W,Q)达到最小,要通过多次迭代过程使其收敛:1) 初始化类中心Qt;2) 固定Qt,找出使F′(W,Q)最小的Wt;3) 固定Wt,用启发式更新算法找出Qt+1使F′(W,Q)达到最小;4) 重复步骤1)2)3),直到类中心不变或目标函数小于阈值为止.
其中,隶属度矩阵W由定理1计算而来,类中心Q的更新由启发式更新算法而来.
定理1.固定Q,在式(10)~(12)的限制下使F′(W,Q)最小,则W的更新为
(13)
MD fuzzyk-modes算法的基本步骤:
1) 随机选取k个对象作为初始类中心;
2) 根据2.1节,计算每个对象到k个中心的距离,将对象分配到与其距离最小的类中;
3) 根据2.2节,计算每个对象到k个中心的隶属度,并更新k个类的类中心;
4) 重复步骤2)3),直到类中心或目标函数不变为止.
算法1.MD fuzzyk-modes算法.
输入:X为由m个属性描述的n维矩阵对象数据,k为需要聚类个数,ε为阈值,idCenters为k个初始类中心的标签,β为模糊因子;
输出:cid是聚类后所有对象的标签,num是迭代次数.
①Q是初始类中心,value=0,num=0;
② whilenum<100 do
③newvalue=0;
④ fori=1 tondo
⑤ forl=1 tokdo
⑥ 计算第i个对象到第l个中心的距离d(Xi,Ql)(用式(4));
⑦ end for
⑧ end for
⑨ fori=1 tondo
⑩ forl=1 tokdo
3 实验分析
为了评价MD fuzzyk-modes算法的有效性,本文考虑了5个真实数据集:Market Basket,Micro-soft Web,Musk,MovieLens,Alibaba.Market Basket记录了1 001个顾客的交易记录,每条记录由用户ID、交易时间、产品名称和产品ID这4个属性描述;Microsoft Web来自UCI数据集,记录了1998年1月份某周内32 711个匿名用户的网页浏览情况,每个用户由用户ID和网页ID这2个属性描述;Musk也来自UCI数据集,包括92个对象,每个对象由167个属性描述;MovieLens从MovieLens网站上下载,本文只使用其中的ratings数据,它记录了6 040个观众对3 900部电影的1 000 209条评分情况,每条记录由用户ID、电影ID、用户评分和提交评价的时间这4个属性描述;Alibaba是884个用户浏览某些品牌的182 880条记录,也由4个属性描述.这5个数据集均为矩阵对象数据集.为了增强聚类效果,本文对各数据集的属性做了相应的预处理,预处理后的数据形式如表2所示:
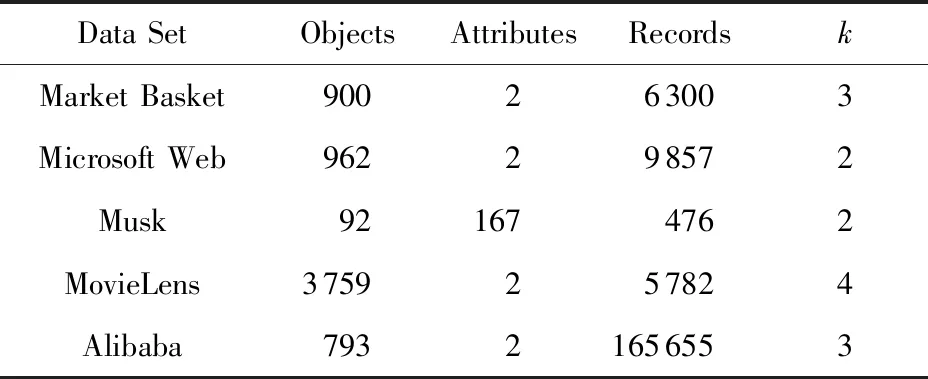
Table 2 Data Set after Preprocessing表2 预处理后的数据集
3.1 评价标准
本文采用精度(AC)、纯度(PR)、召回率(RE)、兰德指数(ARI)、归一化互信息(NMI)这5个评价指标对所提算法进行了有效性评价.AC表示分类正确的比例;PR表示预测为正的样本中有多少是对的;RE表示样本中的正例有多少被预测正确;ARI和NMI用来衡量2个数据分布的吻合程度.AC,PR,RE,ARI,NMI的值越大,聚类结果越接近于数据集的真实划分,聚类效果越好.
设X是一矩阵对象数据集,C={C1,C2,…,Ck}是X的聚类结果,P={P1,P2,…,Pk′}是真实标签,聚类个数为k,真实类别数为k′.假定k=k′,5种评价指标定义为
(14)
(15)
(16)
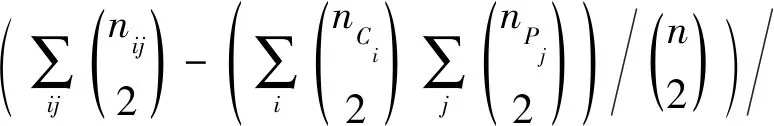
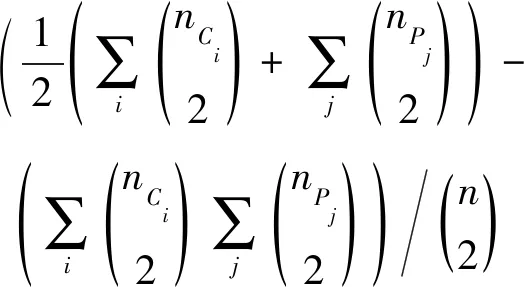
(17)
(18)
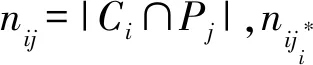
3.2 启发式与全局性更新类中心算法的比较
为了评价启发式更新类中心算法的有效性,本节在用MD fuzzyk-modes算法聚类的过程中,分别采用启发式(HAMF)和全局性算法(GAMF)更新类中心,对比了实验结果与运行时间.以Market Basket为例,运行10次,结果如表3和表4所示.其中,表3的“±”前后分别表示均值和标准差.

Table 3 Comparison Results of the MD fuzzy k-modes Algorithms with GAMF and HAMF表3 在MD fuzzy k-modes算法中用GAMF和HAMF更新类中心的结果比较
Table 4Running Time of the MD fuzzyk-modes Algorithms
with GAMF and HAMF
表4 MD fuzzyk-modes算法中用GAMF和HAMF更新
类中心的运行时间

AlgorithmsRunning Time∕sMD fuzzy k-modes+GAMF3.46725×105 MD fuzzy k-modes+HAMF160.313812
Notes: The bold value represents that the running time of the MD fuzzyk-modes algorithm with HAMF is much shorter than GAMF.
从表3和表4可以看出,用全局性算法更新类中心的聚类效果要好于启发式更新算法,但耗时长达96 h.而启发式更新算法在聚类效果相似的情况下只需耗时160 s.因此,在用MD fuzzyk-modes算法进行聚类时,选用本文提出的启发式更新算法更有效.
3.3 MD fuzzy k-modes算法与其他算法的比较
本文选SV-k-modes,k-mw-modes,fuzzyk-modes,fuzzy SV-k-modes这4种算法与MD fuzzyk-modes算法进行比较,其中,fuzzyk-modes算法必须把矩阵数据转换为单值属性值形式,SV-k-modes,fuzzy SV-k-modes算法需把矩阵数据转换为集值数据形式.在与SV-k-modes,k-mw-modes算法比较时,由于这2种算法不含模糊因子β,本文假定MD fuzzyk-modes算法中的β=1.1.在与fuzzyk-modes,fuzzy SV-k-modes算法进行比较时,由于在fuzzyk-type聚类算法[17-21]中,初始类中心的选取和模糊因子β对聚类结果有重要的影响,不同的初始化类中心和不同的β取值会导致聚类结果不同.本文从这2方面验证MD fuzzyk-modes算法的有效性.在β的取值上,目前很多学者研究这一问题.Pal和Bezdek[26]在fuzzyk-means算法中设置β∈[1.5,2.5],Zhou等人[27]认为β的最优区间是[2.5,3],Huang等人[18]设置最小值β=1.1.由于β的取值没有公认的准则,目前研究的最小值为1.1,最大值为3.本文设置β∈[1.1,2.9],步长为0.2.在初始类中心的选择上,本文随机初始化类中心30次,即2种算法在不同的β取值下分别运行30次,通过计算平均聚类质量来验证MD fuzzyk-modes算法的有效性.数据集Market Basket,Microsoft Web,Musk,MovieLens,Alibaba在这5种评价标准上的实验结果如表5~9所示.其中,“±”前后分别表示30次实验结果的均值和标准差.
从表5可以看出,在不考虑模糊因子β的情况下,新提出的MD fuzzyk-modes算法比SV-k-modes算法、k-mw-modes算法在5种评价标准上的值高,说明聚类效果更好.
表6~9显示,考虑模糊因子β时, MD fuzzyk-modes算法相较fuzzyk-modes算法在5种评价标准上的值有明显提高.尤其是Market Basket和Microsoft Web数据集上,AC,PR,RE,ARI,NMI值有30%~60%的提高,这说明MD fuzzyk-modes算法要比fuzzyk-modes算法的聚类效果好得多.在MovieLens数据集上RE值虽有所下降,但在其他评价标准上有20%左右的提高;Musk数据集的实验结果虽然没有前3个数据集的效果明显,但仍比fuzzyk-modes算法的值高.再者,相较fuzzy SV-k-modes算法,5种评价标准上的值也有所提高.在Market Basket和Microsoft Web数据集上,AC,PR,RE,ARI,NMI值有10%~20%的提高,在Musk,MovieLens数据集上的值相近,但比fuzzy SV-k-modes算法的值高,也说明聚类效果好.
上述实验结果充分验证了MD fuzzyk-modes算法对矩阵对象数据进行聚类具有较好的可行性与有效性.
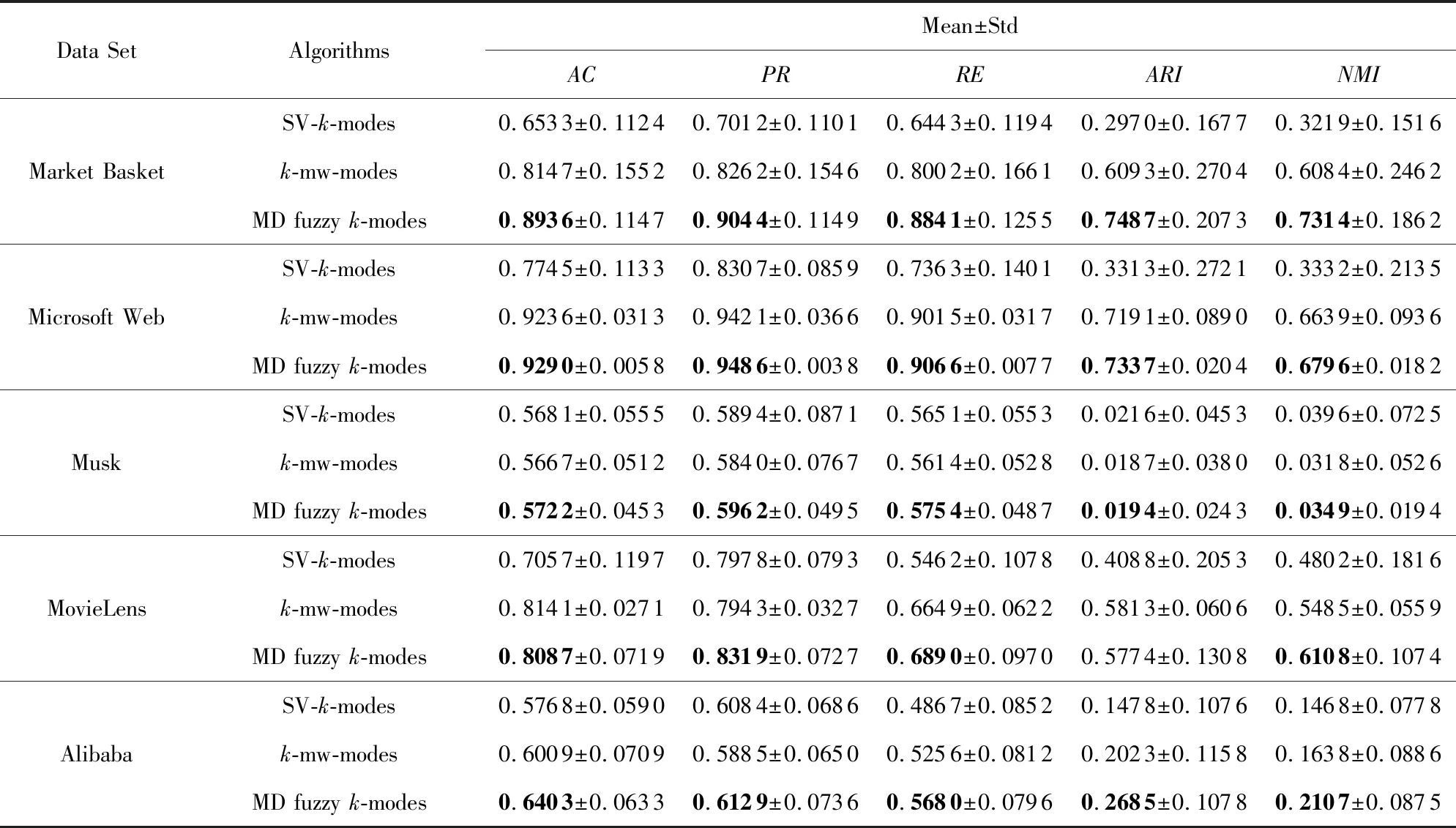
Table 5 Comparison Results of the Three Algorithms on Five Data Sets表5 在5个数据集上3种算法的对比
Notes: The bold values represent that the highest value obtained by the MD fuzzyk-modes algorithm.
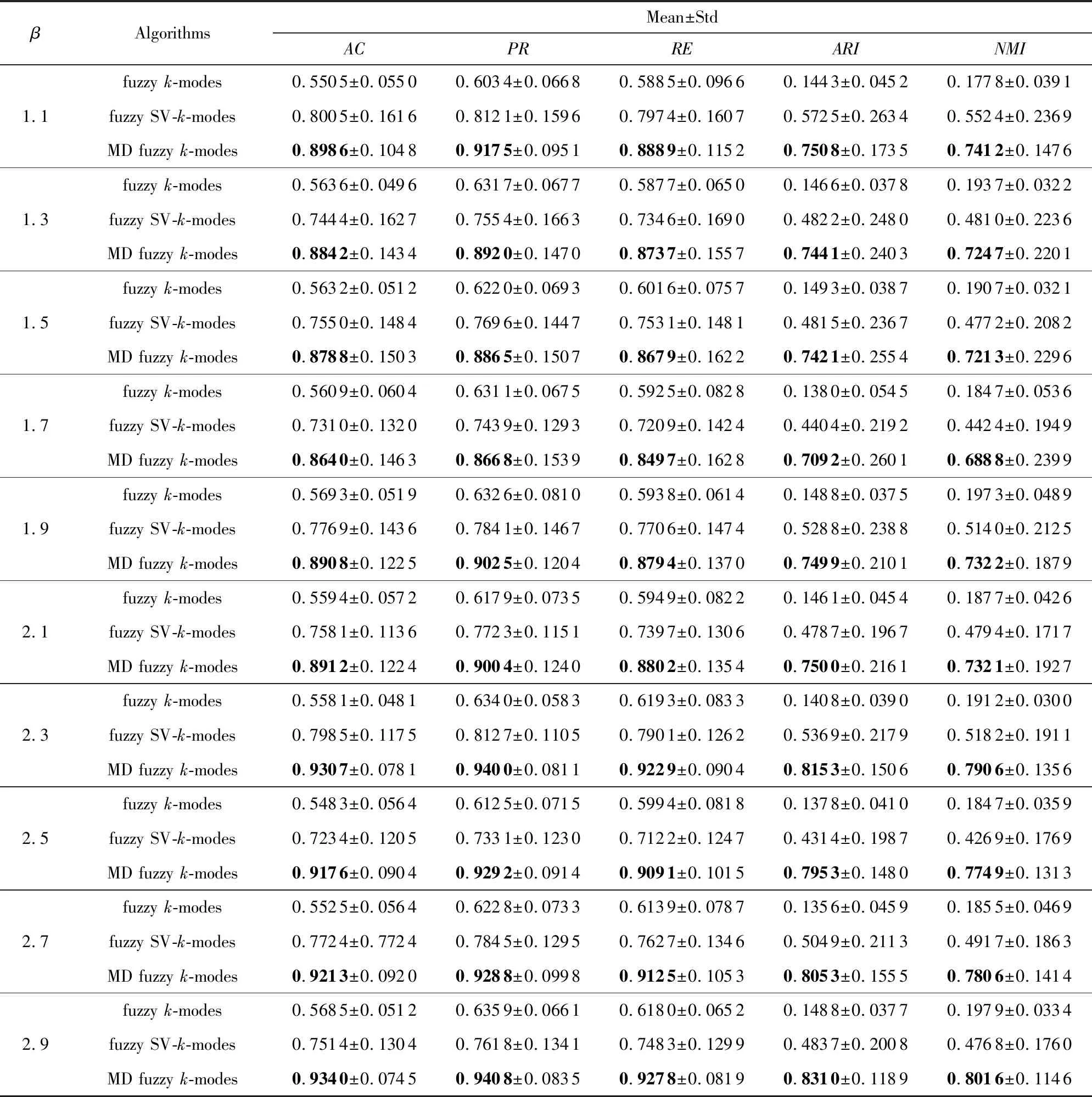
Table 6 Comparison Results of the Three Algorithms on Market Basket表6 在Market Basket数据集上3种算法的对比
Notes: The bold values represent that the highest value obtained by the MD fuzzyk-modes algorithm.
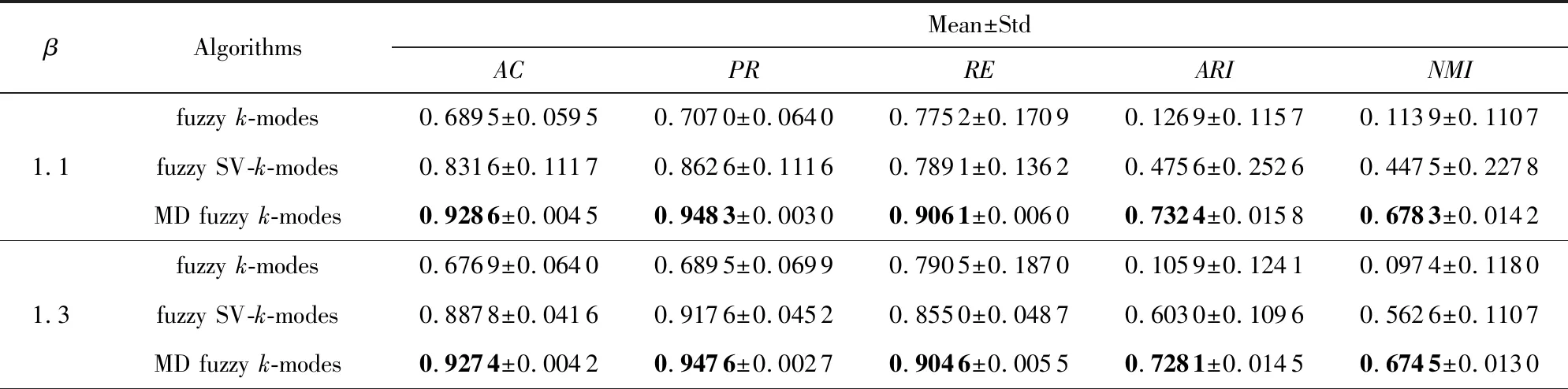
Table 7 Comparison Results of the Three Algorithms on Microsoft Web表7 在Microsoft Web数据集上3种算法的对比
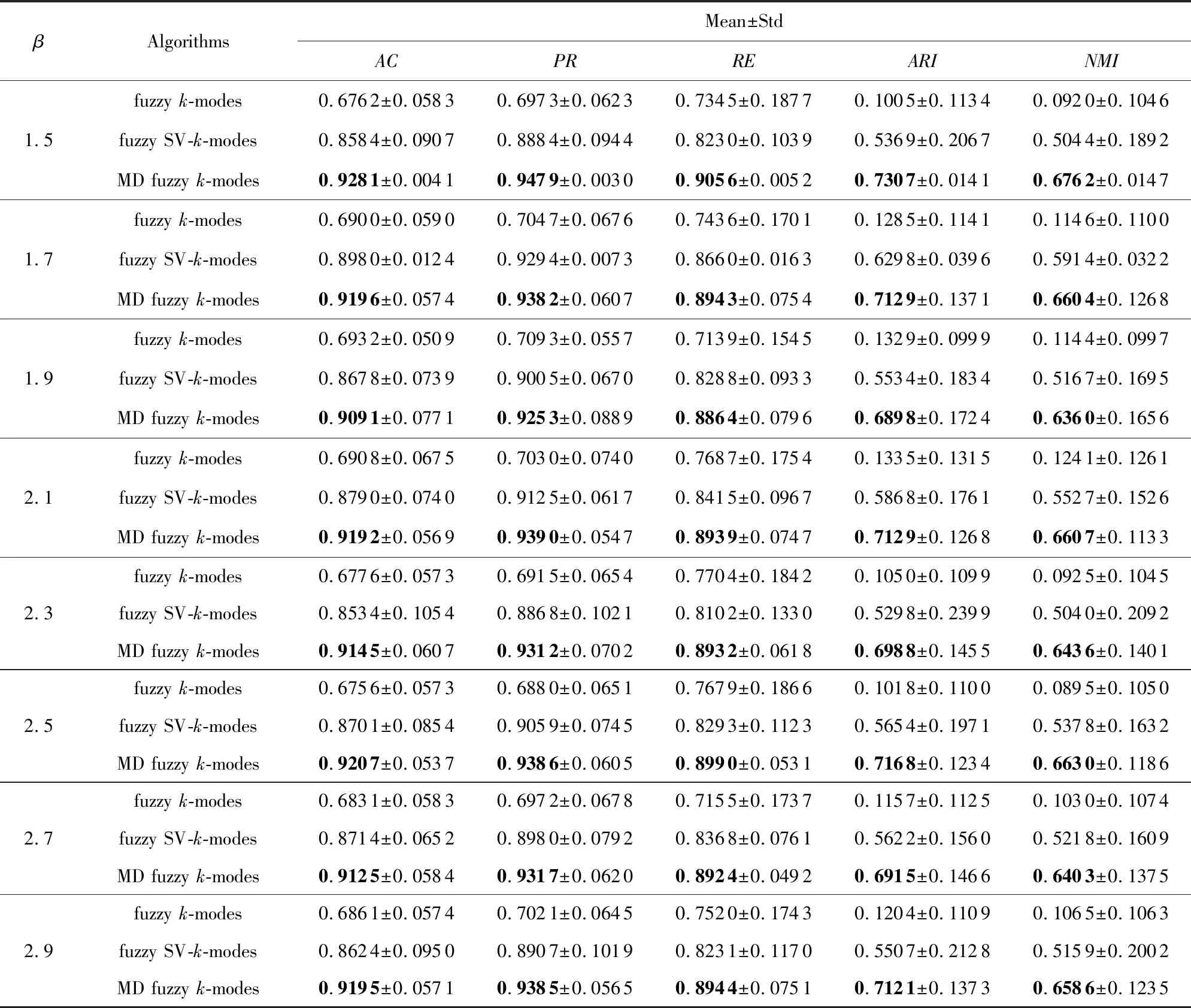
Continued (Table 7)
Notes: The bold values represent that the highest value obtained by the MD fuzzyk-modes algorithm.
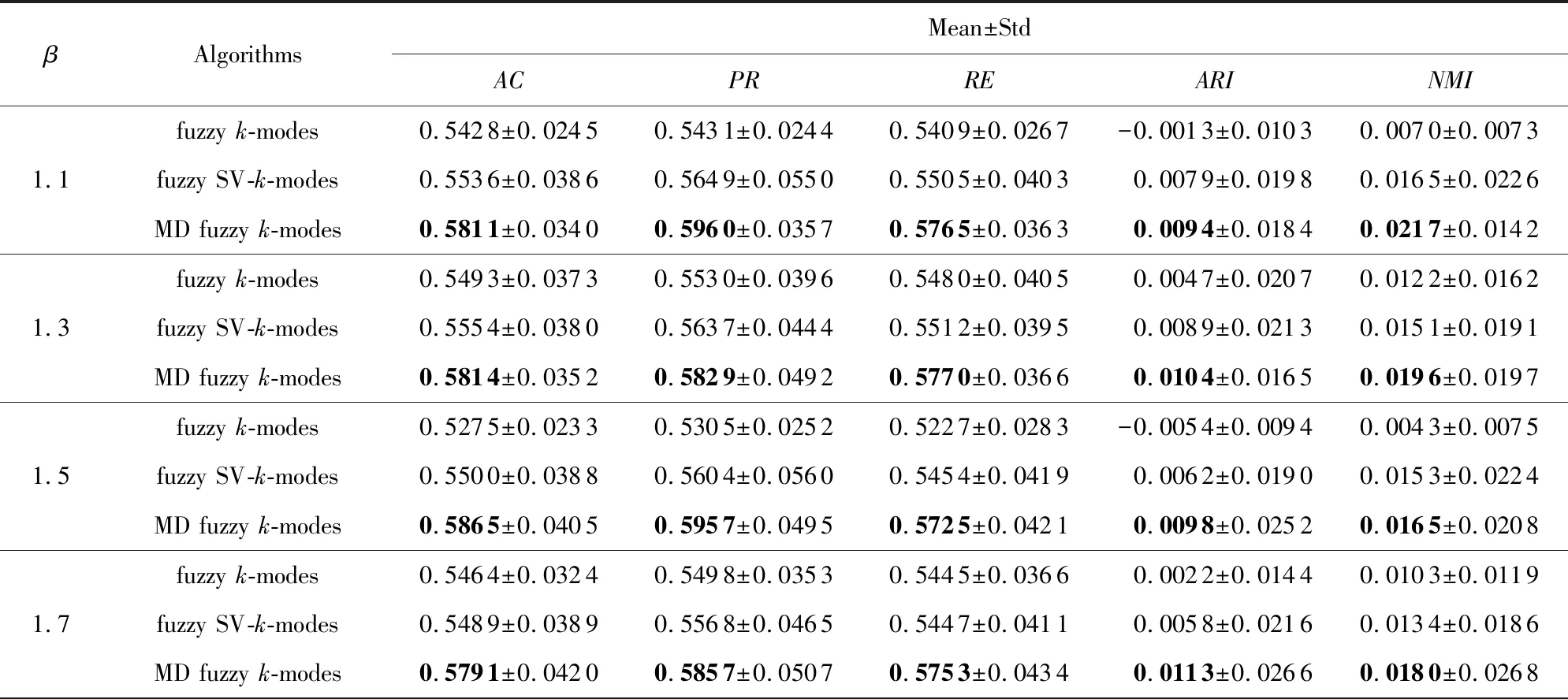
Table 8 Comparison Results of the Three Algorithms on Musk表8 在Musk数据集上3种算法的对比
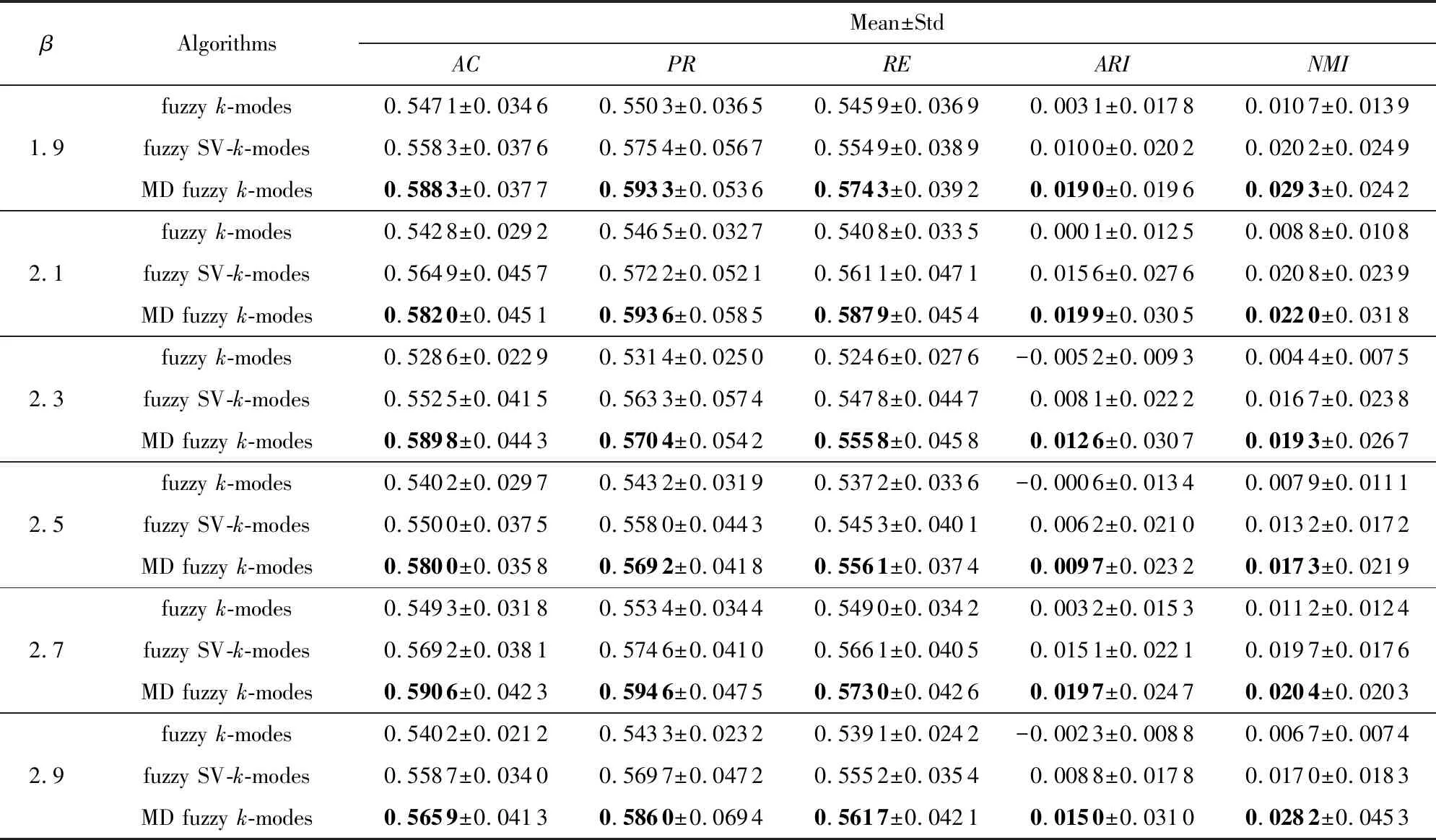
Continued (Table 8)
Notes: The bold values represent that the highest value obtained by the MD fuzzyk-modes algorithm.
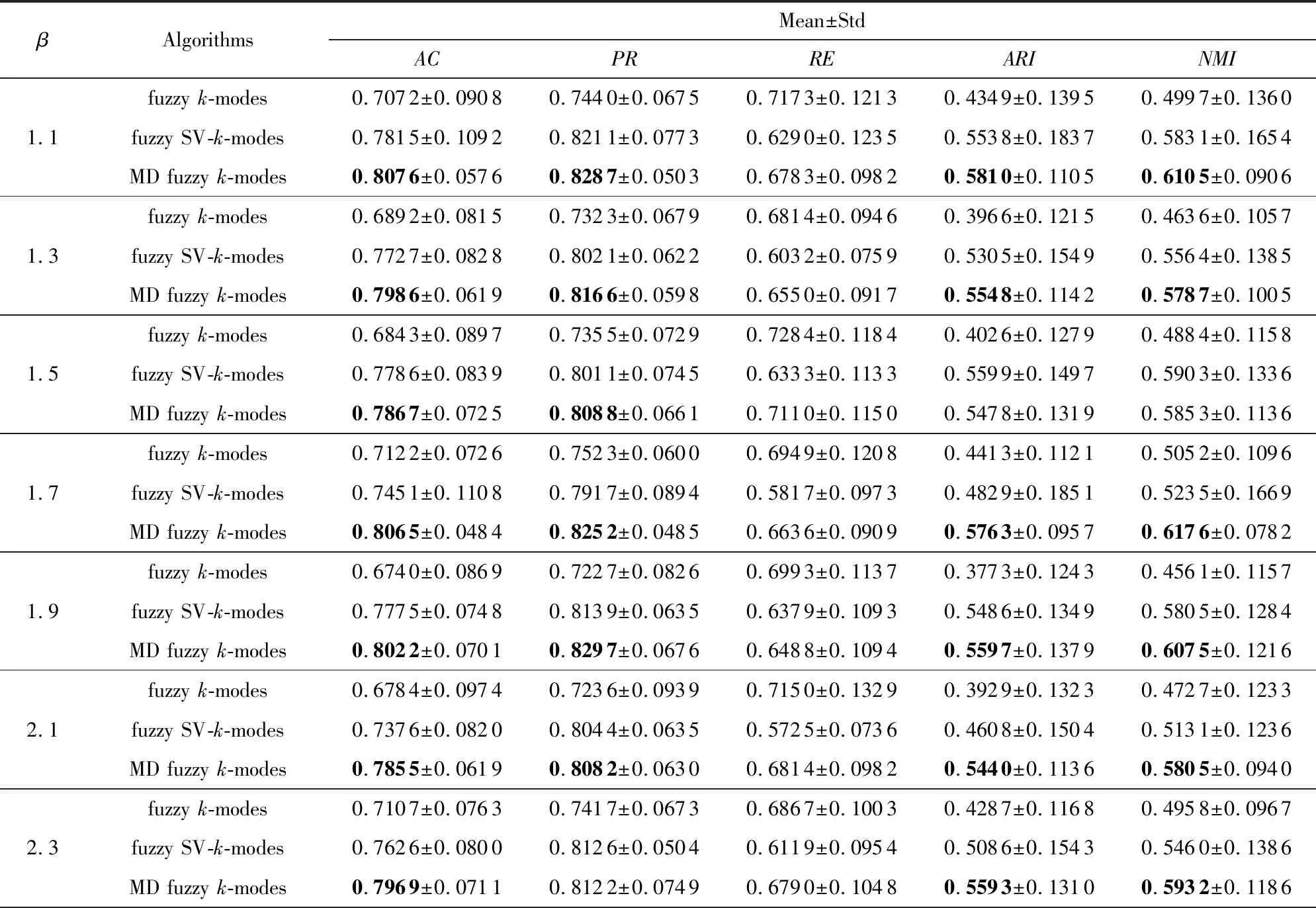
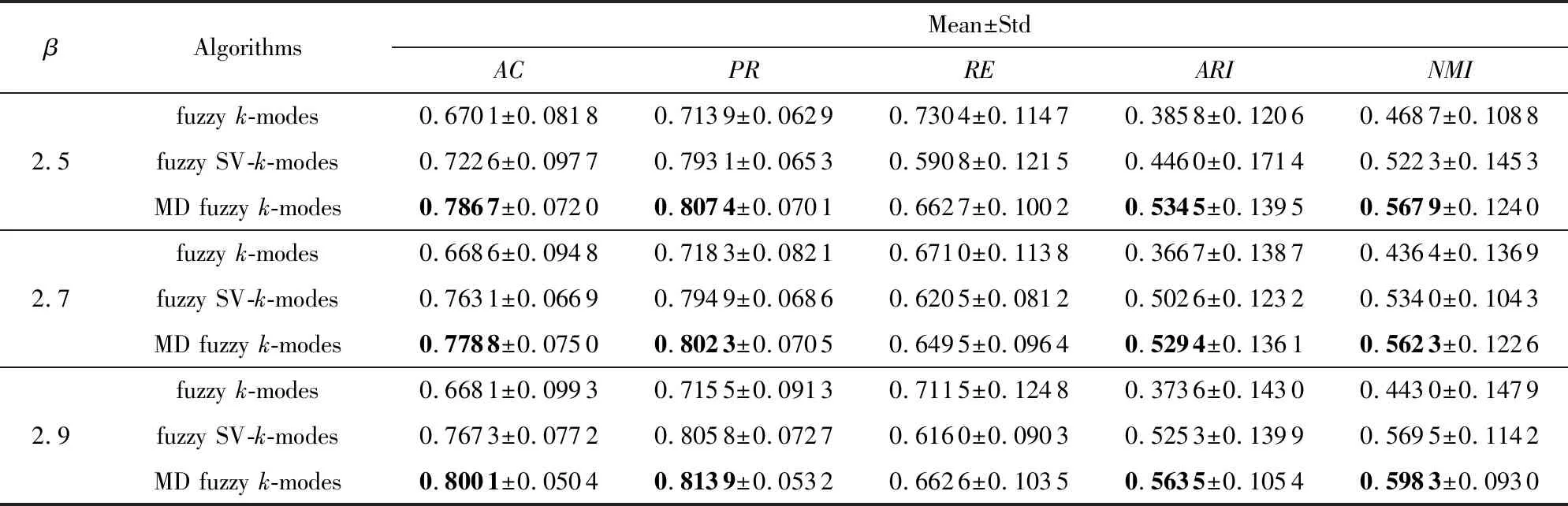
Table 9 Comparison Results of the Three Algorithms on MovieLens表9 在MovieLens数据集上3种算法的对比
Continued (Table 9)
Notes: The bold values represent that the highest value obtained by the MD fuzzyk-modes algorithm.
3.4 β与w的关系
由于β的取值直接影响矩阵对象归属到每个类别的隶属度,因此有必要分析模糊因子β与隶属度w的关系.由于数据集的对象数过多,本文只取前10个对象作为研究对象.经过30次实验后求平均,Market Basket,Microsoft Web,Musk,MovieLens这4个数据集的实验结果分别如图1~4所示.其中,“○”表示矩阵对象分到第1类,“★”表示矩阵对象分到第2类,“□”表示矩阵对象分到第3类,“+”表示矩阵对象分到第4类.
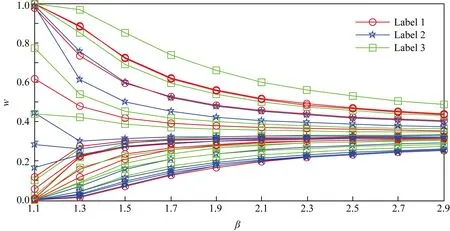
Fig. 1 Relationship between β and w on Market Basket图1 在Market Basket数据集上β与w的关系图
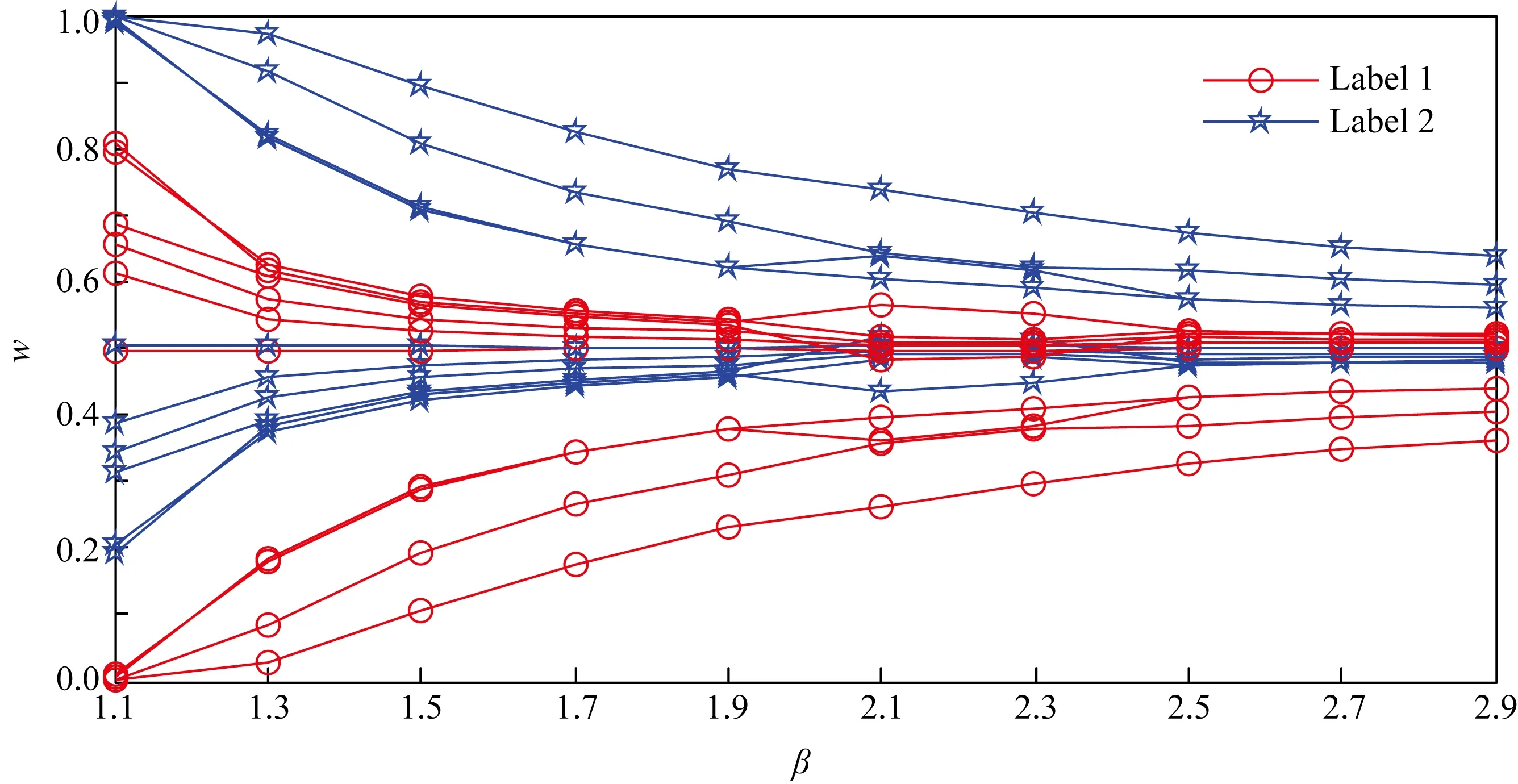
Fig. 2 Relationship between β and w on Microsoft Web图2 在Microsoft Web数据集上β与w的关系图
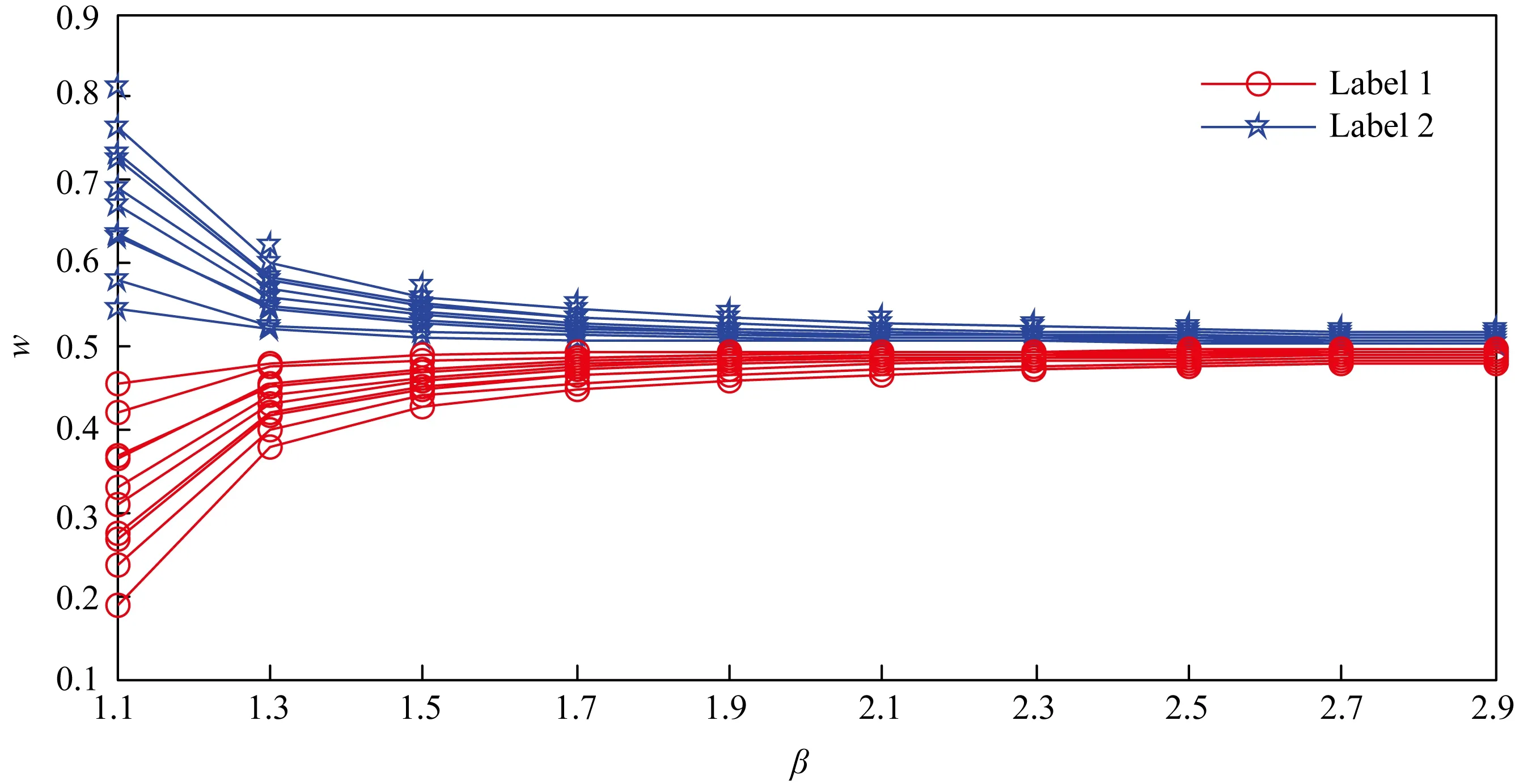
Fig. 3 Relationship between β and w on Musk图3 在Musk数据集上β与w的关系图
由图1~4可知:隶属度w明显受模糊因子β的影响.随着β的增大,w的值呈递减(或递增)形式变化.β的值越大,曲线越平缓,即隶属同一类别的可能性越趋于一致.
4 结 论
实际应用中,大多数数据都是矩阵对象数据,为了对这类数据进行聚类,本文提出了一种新的聚类算法——MD fuzzyk-modes算法.首先,引用了矩阵对象间的相异性度量;其次,给出类中心的表示及启发式更新算法;再次,提出了MD fuzzyk-modes算法;最后通过在Market Basket,Microsoft Web,Musk,MovieLens,Alibaba这5个数据集上的实验分析,验证了本文所提出的MD fuzzyk-modes算法在聚类效果上的有效性并分析了模糊因子β与隶属度w之间的关系.大数据时代,通过MD fuzzyk-modes算法对多条记录进行聚类,能更易发现客户的消费喜好,从而做出具有针对性的推荐.
