无线传感器网络节点位置验证框架

苗春雨 陈丽娜 吴建军 周家庆 冯旭杭

1(杭州安恒信息技术股份有限公司 杭州 310051)2(浙江师范大学网络应用安全研究中心 浙江金华 321004)

无线传感器网络(wireless sensor networks, WSNs)是物联网(Internet of things, IOT)的重要组成部分[1].节点定位技术则是WSN中重要的支撑技术之一，大量场景中缺少位置的感知数据是无意义的[2]，且诸如基于地理位置的路由、拓扑控制和节点部署等技术均以节点的相对或绝对位置为基础[3-4].学者们从不同的方法论角度出发，提出了大量的WSN节点定位算法[5]，这些算法通常由网络中的信标节点为普通节点的定位过程提供位置参考，以估算其绝对地理位置.最常见的节点定位技术分类方法是按照定位过程是否需要测量节点间的距离分为测距(range-based)算法和非测距(range-free)算法2类[6].在实际应用场景中，信标节点提供的位置参考并不总是可靠的[7]，而传统的定位算法不考虑信标提供的位置参考信息可靠性问题，导致众多性能表现优异的节点定位算法无法适用于信标位置不可靠的场景[8].为解决位置不可靠的信标节点带来的定位精度下降导致网络服务质量降低的问题，提出一种适用于2类定位算法的轻量级信标位置验证方法，作为底层框架(无须采集原定位算法所需的额外参数，同时具有可重用性)，对传统定位算法提供不可靠信标过滤服务，以扩展传统算法的应用范畴.据作者所知，在节点位置验证方面的已有工作，很少在纵向上将3类不可靠信标和横向上的2种测距技术进行统一考虑.

本文的主要贡献有3方面:

1) 提出了一种适用于多种不可靠信标节点共存的节点位置验证框架，为实现可靠的定位提供底层服务；

2) 提出的框架支持测距和非测距2类传统节点位置算法，具有较好的普适性；

3) 节点可信定位框架利用了群智感知信誉模型，具有轻量级分布式的特点，适合大规模的、计算能力有限的无线传感器网络应用场景.

1 相关工作

针对信标位置不可靠问题展开的WSN节点位置验证方法可分为2类：1)漂移信标和恶意信标方面的研究；2)针对定位过程的重放攻击(以虫洞攻击为代表)方面的研究.

以漂移信标和恶意信标为主要研究目标的研究工作分为可容忍测距异常值的算法[9]及带有可靠信标选择的定位算法[10].前者比较适用于存在测距信息干扰和信标移动距离较小的场景.这类算法的主要思想是降低不可靠信标的定位参考作用，但当参考位置误差较大时，算法的定位精度严重下降.可靠信标选择即对位置不可靠的信标进行过滤，以排除其对定位过程的影响.文献[11]提出一种可以应用于任何测距技术的点对点位置验证算法，但需要配备GPS的节点作为校验节点，文献[12]也采用类似的方法，由AP节点进行集中式的节点位置校验，以实现可信的定位.文献[13]提出基于Huber损失函数的恶意信标节点检测算法，具有高效且轻量级的特点，属于可信的测距定位算法.He等人[14]则提出一种应用于到达时间(time of arrival, TOA)测距技术的、可排除异常测距值的可信定位算法;而文献[15]中提出的恶意信标过滤机制也是基于TOA或到达时间差(time difference of arrival, TDOA)测距技术，采用每个节点在自己的视角通过准确地测距构建局部坐标一致集，通过对局部坐标一致集的合并，排除恶意信标.而对接收信号强度指标(received signal strength indication,RSSI)测距技术，由于其测距本身的误差，对可信定位算法的设计带来更大的挑战.Kuo等人[16]提出的信标移动检测算法(beacon movement detection, BMD)，主要用来识别网络中的部分位置发生被动改变的信标节点.其思路为：在网络中设置一个BMD引擎来收集全网络的RSSI信息并进行处理，在一定容错范围内能够识别出信标节点的位置是否已发生移动.但集中式的算法因其计算量较大，且在信息收集阶段产生大量的通信开销，不适用于由随机撒播部署的网络连通度较高、规模较大的WSN网络；也有一些集中式的算法，采用隐藏的位置校验节点对信标位置进行验证[17]，由于需要额外的可信节点作为检验者，导致其普适性不高.文献[18-19]运用图论中的刚性理论作为节点间相互位置的基本原理，用于排除定位过程中的位置参考异常值，确保节点定位的可信性，但此类方法运算量较大，且刚性理论对节点间测距精度有很高的要求.Garg等人[20]采用识别和排除在节点定位算法收敛过程中提供了较大下降梯度的信标节点，提高定位结果的可信性，但由于算法只依赖信标节点，缺少对普通节点位置的参考，不太适用于信标节点稀疏的WSN，且也存在计算开销较大的问题.Ansari等人[21]也采用了相似的方法，并存在同样的问题.文献[22]采用分布式的信誉模型设计可信定位算法，但对网络的变化需要较长的反应时间.Wei等人[23]根据邻居节点间的相互观测信息建立了位置验证概率模型，并取得较好的效果，但也只适用基于测距的定位算法.文献[24]运用分布式的基于RSSI变化的邻居节点评分机制来识别位置被动改变的信标节点，但不能运用于信标节点被诱捕的情况.文献[25]则通过凸优化方法，对主动提供不可信位置参考的信标进行识别，但也存在集中运算导致计算量过大的问题.

而另外一些工作则将可信定位的重点放在抵抗攻击的安全定位方面，最典型的是抗虫洞攻击的定位算法，代表了信标节点信息被重放的外部攻击类型(恶意节点属内部攻击)[26].文献[27-28]对WSN节点定位方面的安全威胁和安全算法进行了综述.文献[26]对常见的攻击方法进行了分类，并将现有的安全定位算法进行分类比较；而文献[27]则重点描述了威胁的类型；文献[28]不但将安全定位算法进行了综述，同时将节点位置验证的方法进行了介绍.Lazos等人[29]的工作分析了虫洞攻击、女巫攻击和捕获信标节点的攻击对定位过程的影响，采用方向天线和加密等技术提供安全可信的非测距定位方法.文献[30]提出的安全定位算法则适用于基于测距的定位场景，能够通过距离约束完成恶意节点检测和抵抗虫洞攻击，但属于集中式的算法.Dong等人[31]的工作则阐明由于虫洞攻击改变局部的网络拓扑结构，则可利用拓扑结构信息检测虫洞攻击；而文献[32]的工作与其类似，利用网络连通度的一致性检验来检测虫洞攻击.Che等人[33]针对安全定位(主要考虑虫洞攻击引起的信标重放问题)做了连续的工作，包括提出利用节点间的距离约束抵抗虫洞攻击，属于基于测距技术的安全定位算法.在文献[34-35]中分别提出利用节点间的3种数据传输特征：1)发送数据自我排斥特性；2)邻居数据接收唯一性；3)传输距离约束，进行测距定位技术下和非测距定位技术下的虫洞攻击检测算法.Bao等人[36]则运用证据理论进行节点可信值计算，采用博弈论算法按节点可信等级进行分类，排除对定位影响较大的恶意信标节点，以抵抗信标重放攻击提高定位精度.

目前的研究工作虽然在非测距WSN节点定位算法的信标位置验证问题上取得的进展较少，还是对解决由信标位置不可靠引起的定位质量下降问题提供了借鉴.存在3方面问题：1)研究成果无法同时适用于基于测距和非测距的定位算法，不具备通用性；2)集中式算法能够提供全局视野，但不符合大规模WSN分布式计算的需求；3)现存的大量节点位置验证方法均只针对某种特定场景进行研究，可谓各自为战，并没有将存在3类不可信的信标进行统一考虑和解决，因此，提出的方法缺少普适性.

2 问题描述与解决思路

2.1 相关定义

WSN部署到特定场景后，出于成本的考虑，往往只给部分节点配备GPS或预先定义其位置，使其成为信标，其他节点依靠信标广播的位置作为参考，通过特定的算法估算自身位置.因节点位置可能因为外界原因而发生改变，在每个时间周期T重新定位，即可完成位置校准，但在校准过程中，若信标提供的位置参考是不可靠的，则定位质量会严重降低.我们定义3类位置不可靠的信标.

定义1.漂移信标.在某些应用场景中，网络部署并完成节点定位后可能发生节点自身位置发生被动的改变(如被动物影响等)，这种现象叫作节点漂移，发生漂移的信标称为漂移信标.

定义2.虚假信标.信标节点广播的Beacon信息被通过某种方式在网络的另外区域重放，使得原来不能接收到该Beacon信标的节点误以为有1个可用信标，这种被信息重放影响而多出来的信标节点称为虚假信标.

定义3.恶意信标.信标节点因为内部软件错误或硬件故障，造成其广播的位置参考信息与其实际位置信息不一致；或在敌对环境中(如战场环境)，某些信标节点可能被敌方捕获，而故意广播虚假的位置参考信息.这种主动或被动地提供错误位置信息的信标节点，均被认为是恶意信标.

定义3的场景可由虫洞攻击而出现，如图1所示.图1中A1和A2为2个信标节点，相互间的距离大于通信半径，S1和S4处于A1的通信范围之内，而S2，S3处于A2的通信范围之内；通过S1与S2这2个节点实施虫洞攻击，将各自听到的Beacon信息通过特殊的链路(可以是有线连接[37])双向重放，使得S3和S4分别收到来自A1和A2的Beacon信息，使得各自的通信范围内存在1个虚假信标节点.

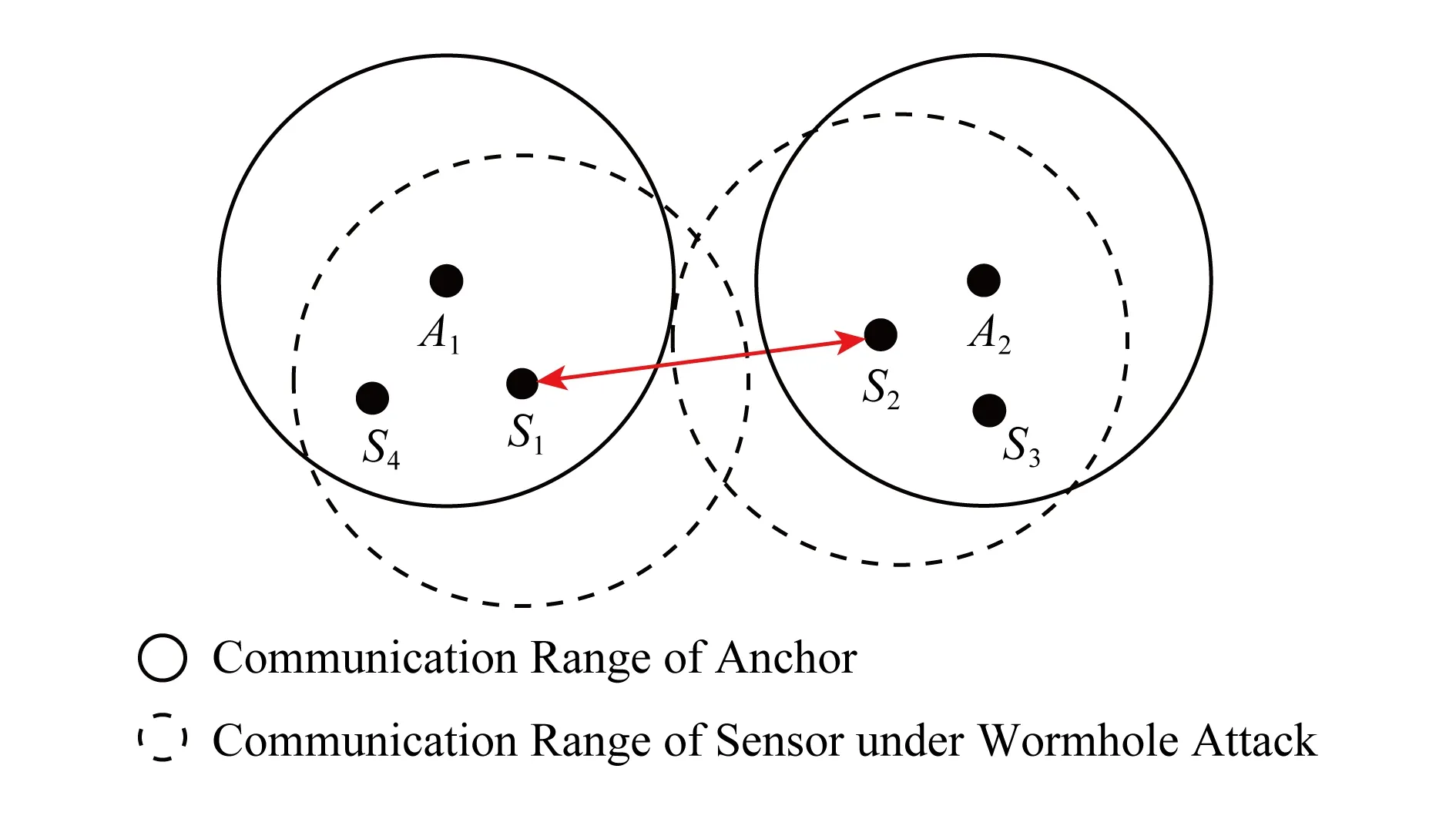
Fig. 1 False beacon suffered from worm-hole attack图1 受虫洞攻击而出现的虚假信标

可见，漂移信标、恶意信标和虚假信标均是位置不可靠的信标，其中恶意信标属于内部攻击，另外2种属于外部攻击[37]，恶意信标相对来讲更加难于检测，因其不会以合作的态度参与到检测过程.

2.2 问题建模

2.3 解决思路

节点位置验证框架(node location verification framework, NLVF)的实现思路是将每个节点对其邻居的位置观察结果与其他节点的观察进行综合，得到某一特定节点位置可靠性的判断；用带有直接和间接信誉的模型来表征这2种观察结果，并依靠2种信誉值计算综合信誉值来表征节点位置的可靠程度.计算过程中通过带有可信度更新机制的间接信誉计算方法克服恶意评价的影响.为使其适用于基于测距和非测距的2类定位算法，在直接信誉值计算过程屏蔽2类算法的距离表达差异.NVLF结构如图2所示:

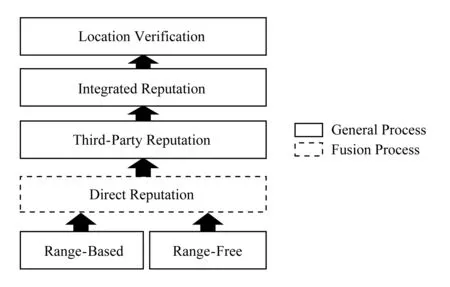
Fig. 2 Framework of location verification图2 位置验证框架结构图

3 分布式位置信誉模型

3.1 距离的定义

NLVF以节点间的相互位置观测结果作为分布式信誉模型的构建基础，而节点间的位置相互观测则以距离作为度量，对于测距技术的定位算法，节点i可测量与其能够直接通信的信标节点j之间的信号特征计算2点间的距离δij，比如在基于RSSI的定位算法中，可计算测量距离δij[38]:

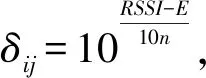
(1)

其中，E为基础信号强度，通常取1 m距离上的接收信号强度；n为损耗系数，取值范围为[2,4](真空中取2，干扰较大的环境取4).

Fig. 3 RSSI vs. distance under ideal condition图3 理想情况下RSSI与距离的关系

Fig. 4 RSSI vs. distance under ideal condition with identical orientation of different nodes图4 理想情况下不同节点在同一方向上RSSI与距离的关系

图5则是在行人和车辆随机经过实验场景的情况下，经过高斯过滤后的3个节点的RSSI平均值曲线.可以看出RSSI受到较大的影响，当节点间距较近时，RSSI基本上反映出这种距离的远近关系;但当节点相距较远时，表现则不明显.这也为基于分级制的跳数划分提供了依据.

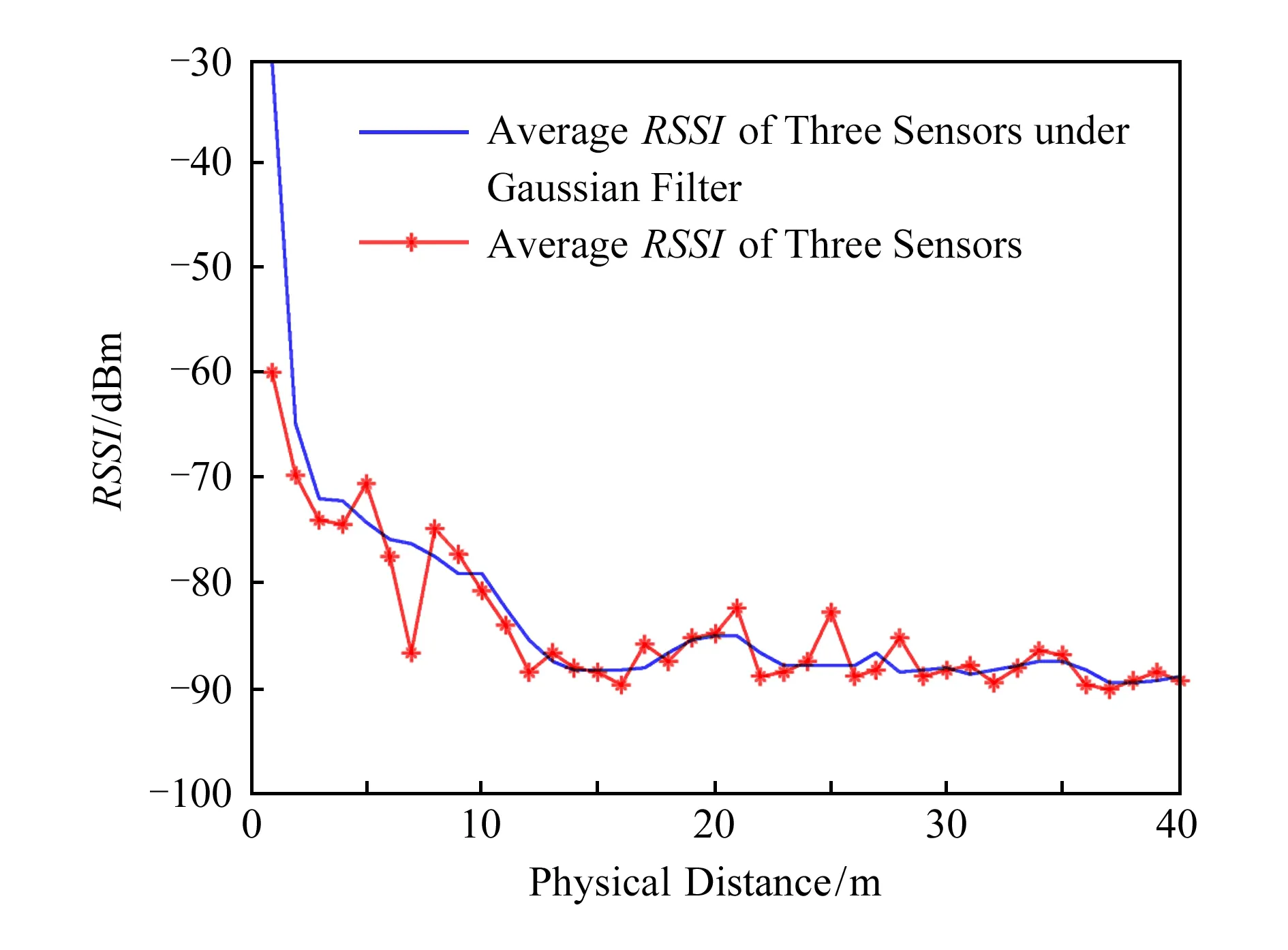
Fig. 5 RSSI vs. distance under severe interferences图5 严重干扰情况下RSSI与距离的关系

因此，本节用log函数定义节点间跳数：

(2)

其中RSSI(i,m) min为节点i接收到其邻居的所有RSSI值中的最小值.式(2)没有采用固定的RSSI作为基准而是采用节点接收到的RSSI最小值，有效地表达了局部观测结果，本算法的分布式特性与这种局部表达高度吻合.

采用式(2)，相当于将节点间的距离进行了等级划分，克服了采用0-1模型带来的输入过于简单的问题；而对数形式的节点间距离划分，又较好地表达了RSSI与距离之间的关系.假设1对节点Si，Sj之间传递了若干数据包，采用Dixion准则进行异常值的过滤后按式(2)进行计算，对应的距离等级集合表达为Vi={v1,v2,v3,v4,v5},i=1,2,…,n，表示对节点之间的距离的等级划分，其中v1,v2,v3,v4,v5可看作表示近、较近、较远、远、很远.

假设Ui={u1,u2,u3,u4,u5},i=1,2,…,n，表示2节点间收发的RSSI强度， 我们用模糊评价矩阵M表示U和V之间的模糊关系，其形式为

(3)

假设SA节点向SB节点发送n个RSSI数据报，rij表示在当|SA,SB|∈vi时其RSSI数据报中在Uj对应的RSSI值范围的个数为m，rij=mn.

获得模糊评价矩阵M后，假设S1接收到S2的n个RSSI数据时，计算其在u1,u2,u3,u4,u5对应RSSI范围的概率分别为a1,a2,a3,a4,a5，通过F(∧,∨)计算得到模糊评价向量(b1,b2,b3,b4,b5)，其计算为

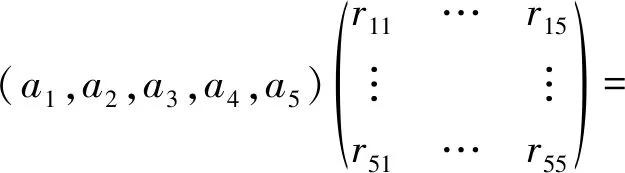
(4)

最终按照最大隶属度原则，获得最终的距离评级vk.

算法1.基于RSSI值的节点距离模糊划分算法.

输入：RSSI;

输出：距离等级.

Step1. 通过实验获得RSSI-距离模型以及通信范围；

Step2. 构建距离等级V和RSSI-距离关系U，计算模糊评价函数；

Step3. 节点与邻居节点互相发送n个RSSI值数据包；

Step4. 节点将收到的RSSI值数据包计算得到对应V中距离等级的概率分布向量A；

Step5. 计算得到模糊评价向量B=A·M=(b1,b2,b3,b4,b5)；

Step6. 按照最大隶属度原则，得到距离等级B(vk)=max(b1,b2,b3,b4,b5).

若要将算法1定义的跳数转化为传统非测距定位算法中以小于1的实数定义的跳数，可计算为

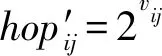
(5)

其中vmax为跳数估算的广播阶段中节点收到的等级划分最大值.

3.2 直接信誉值

(6)

不同的测距技术使得δij虽然包含一定的误差项(如采用超宽带技术下的TOA测距时误差较小)，但其能够反映相对真实的节点间距离.但当节点进行相对较大位移的漂移或广播明显错误的位置参考时，邻居节点对其的信誉值下降.式(6)很好地体现了距离越接近的节点，相互测距越准确的实际情况[38]；同时，对于新加入的邻居节点采用不信任原则.

而对于非测距技术来讲，我们虽然将节点间的距离按RSSI值表达成等级划分，但带来的问题是当2节点本身相距较远时，该距离等级对应的距离也较长，又因节点通信半径较大，会出现节点位置改变后仍处于同一等级的问题，即距离变化不敏感的问题.

Fig. 6 Relationship between distance and rank图6 距离等级变化示意图

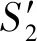
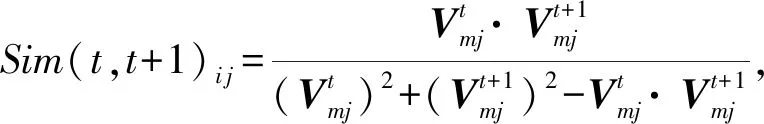
(7)

Jaccard系数法源于余弦定理，但能够克服除数为0的情况.

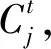
(8)

下文中可以看到，在信誉模型中，间接信誉值也是根据直接信誉值计算并迭代更新的，因此，采用不同的方法计算直接信誉值后，测距的和非测距的可信定位框架在其他运算过程均一致，体现了其普适性.

3.3 间接信誉值

WSN中因随机冗余部署的原因，每个节点都有多个邻居节点，Sj(t)表示在时刻t能够和节点j直接通信的节点集合.只要Sj(t)中的节点将自己对j的信誉度局部广播给其2跳邻居，就能确保本集合之中所有节点均能相互交换对节点j的信任度，对节点i来讲，综合计算其收到的其他节点对j的信誉值，通过一定的计算可以得到反映其他邻居节点对节点i的定位精度的信任程度.计算方法为

(9)

其中,Rmj(t)表示时刻t节点m对节点j的信任度，Cim(t)表示时刻t在节点i的视角上节点m的推荐可信度，Rmj(t)定义为

Rmj(t)=Dmj(t),

(10)

而Cim(t)的计算相对复杂，无法从节点i的视角直接得到，因为要考虑到其他节点可能产生漂移而引起的间接可信度恶化的情况.如图7所示，时刻t节点S5已经产生漂移，但节点S1与节点S5的相对距离并无改变，因此，可以获得较高的DS1,S5(t)，而节点S5与节点S2，S4的距离变化将导致S1来自S5视角的对S2，S4的推荐度较低.而根据式(8)，因节点S3第1次能够与S5通信，在S1的视角上，S3获得的来自S5的间接信誉值为0，因此，必须采取一定的推荐可信度更新机制，使得节点间的相互观察能够收敛至稳定可信.

Fig. 7 Circumstance of identical direct reputation图7 直接信誉值不变的情况

为解决上述问题，我们引入信任度更新机制[40]，首先计算节点信誉差Dif和相对信誉偏差RTD为

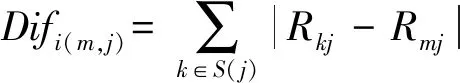
(11)

RTDi(m,j)=Difi(m,j)STDj,

(12)

其中，Difi(m,j)表示在节点i的视角下，节点m对节点j的信誉值偏差；|S(j)|表示集合S(j)的基；STDj表示S(j)中所有节点对节点j信誉值的标准方差.当RTDi(m,j)≤1时，节点i认为节点m对节点j的位置可信度判断与其他节点一致；否则，认为节点m产生了间接可信度恶化的现象.Cim(t)根据RTDi(m,j)进行更新的计算式为

Cim(t)=

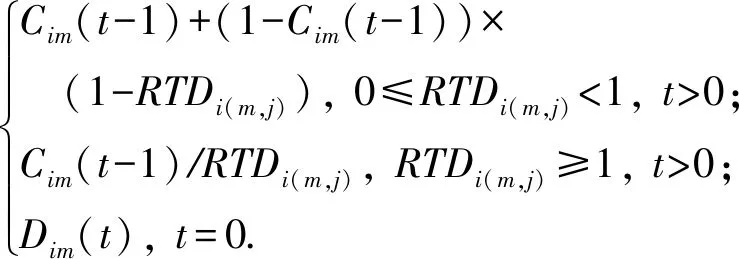
(13)

信任度更新机制将降低节点漂移或不可靠信标节点对间接信任值计算的影响.

3.4 综合信誉值

在时刻t，当节点i计算得到节点j的直接信誉值Dij(t)和间接信誉值Iij(t)后计算其综合信誉值Tij(t):

Tij(t)=αDij(t)+(1-α)Ii,j(t),

(14)

其中,α为信誉值权重，其大小解决了对自己的判断和其他节点的推荐信誉值的依赖程度.当节点本身发生漂移或2节点同时漂移且相对距离变化不大时，如果α值较大时，易造成位置验证的性能下降；若α取值过小，则受到其他节点的误判影响较严重.关于α的取值将在第5节通过仿真实验进行讨论.

4 节点位置验证框架

基于分布式信誉模型的可信定位基本思路如图8所示，节点i通过其他节点信誉值所反映的位置可靠程度来判断其他节点是否可信；通过对直接信誉值和间接信誉值的一致性来判断自身是否产生了漂移.若节点i自身产生了漂移，则在排除了不可靠的信标节点后，通过重新调用定位算法进行位置验证，如果重定位过程中可用信标数小于定位算法的最低要求，则通过基于信誉值的临时信标择算法进行信标补充.因不可信信标的存在，网络部署后，位置验证和重定位是周期性进行的，因此以位置验证为目地收集到的RSSI信息同样服务于重定位，因此，并没有额外的通信开销.下面按顺序对可信定位中的2个处理环节(即节点位置的验证与重定位)进行详细说明.

Fig. 8 Flow chart of NLVF图8 NLVF工作流程图

Fig. 9 Schematic diagram of reputation in reliable localization图9 可信定位过程信誉值示意图

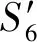
5 实验结果与讨论

仿真环境在500 m×500 m的正方形区域内，随机部署n个普通传感器节点和m个信标节点(每对信标节点的间距不小于5 m).所有节点具有相同的通信半径r=50 m.在网络成功部署及初始定位完成后，有m′个节点成为位置不可信节点，它们位置的改变大于20 m，其中被捕获的信标节点比例不高于50%.所有实验结果为50次实验的平均值.

5.1 算法参数选择

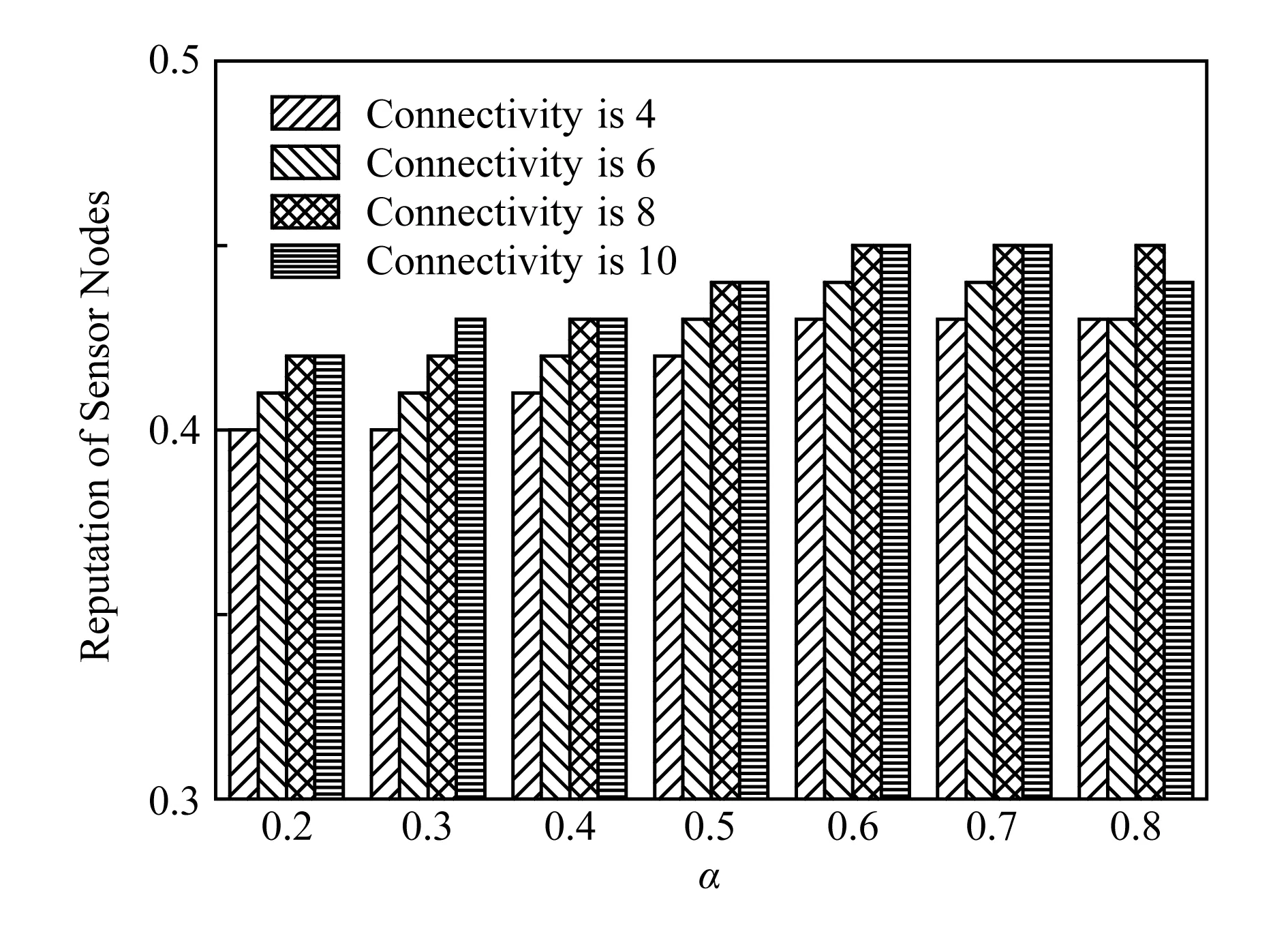
Fig. 10 Average mean variation with 10 percent unreliable anchor图10 位置不可靠信标占比10%时信誉值平均偏差

信誉值计算公式中权重参数α的取值难以利用封闭表达式进行描述，在产生漂移的节点和不可靠信标数量比重变化的场景中，对α不同取值情况的算法性能进行了仿真.因为节点的直接邻居数量对间接信誉值的准确性也有影响，故实验中也对平均网络连通度进行了调节，范围为[4,10]，步长为2.信标节点占比10%，位置不可信节点数的比重从10%～40%变化，步长为10%.实验中将节点间的测距精度设定为0.1r，对位置可信节点和位置不可信节点的平均信誉值average(Trel)及average(Tunr)进行计算，结果如图10～13所示:

Fig. 11 Average mean variation with 20 percent unreliable anchor图11 位置不可靠信标占比20%时信誉值平均偏差

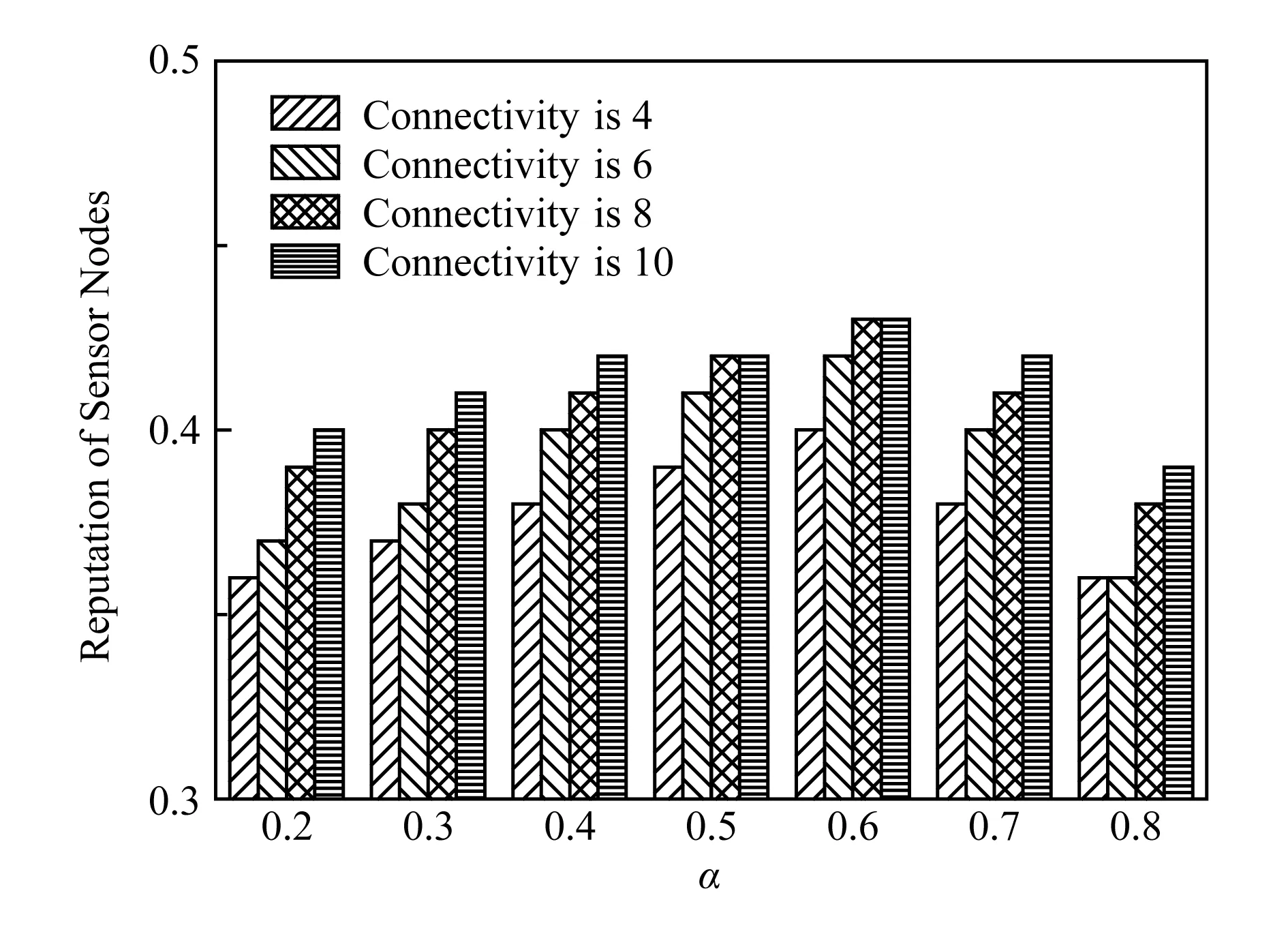
Fig. 12 Average mean variation with 30 percent unreliable anchor图12 位置不可靠信标占比30%时信誉值平均偏差

Fig. 13 Average mean variation with 40 percent unreliable anchor图13 位置不可靠信标占比40%时信誉值平均偏差

图10～13中纵坐标为产生位置不可信节点3个时间片后average(Trel)-average(Tunr)的值，我们称之为Diffave.可以看出，2种节点的信誉值之间存在着明显的差异，当位置不可信的节点占比升高时，差异变小，但也足够明显，这也是采用分布式信誉模型进行位置验证的基础.这种差异随着网络连通度的提高也会变得明显，特别是当连通度大于6，而α∈[0.4,0.6]时.综合看来，α=0.6时，Diffave的值始终大于0.38，因此，实验中α=0.6.在不同的RSSI测量误差情况下对检测阈值ω的取值进行了实验，仿真场景中网络平均连通度设置为8，信标占比10%，发生漂移的普通节点比例与不可靠信标的比例均为20%，节点采集的RSSI数据噪音为[0.1,0.3]，步长为10%，结果如图14所示：

Fig. 14 Threshold vs. detection performance图14 检测阈值与检测性能的关系

我们用来衡量漂移检测算法性能的2个指标为：识别成功率及识别错误率，计算公式为

(15)

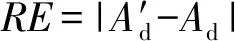
(16)

识别成功率为被正确判断为漂移节点的数量与实际漂移节点数量的比值，用来衡量算法能够成功识别位置不可信节点的概率；而错误率则是被错误地判断为不可信节点的数目与实际不可信节点数目的比值，用以衡量算法在检测漂移节点时产生误判的概率.实验结果显示的是实验过程中每个时间周期的检测成功率和错误率取平均值.非测距算法中RSSI的噪音由经典信号能量传播衰减模型为基础，衰减指数n=2.5，上下随机产生百分比变化，如20%的噪音，则n值变化范围是[2,3].

从图14中可以看出，当检测阈值增大时，检测成功率和检测错误率均呈上升状态，因为检测条件变得苛刻后，成功率必然升高，但由于误差的存在检测错误率也随之升高；综合来看，ω取值为[0.7,0.8]之间时，算法性能较好，因此，后续实验中设置ω=0.7；另外，随着RSSI噪音的增加，检测错误率有很小的上升，检测成功率却影响不大，这也充分验证了UNDA的鲁棒性，RSSI具有30%的噪音情况下检测成功率能够达到90%以上.

5.2 位置验证效果

为了验证可信定位模型中用于服务基于测距技术的不可信信标检测性能，我们用同样是分布式位置验证算法的文献[24]作为比较对象，简称为节点漂移检测(node drifting detection, NDD)算法.设置40个信标节点，仿真中每个时间段内均有随机数量(0～20%)的节点发生漂移或变为恶意信标，但漂移节点总数不变，随机出现1～4个虫洞(对应2～8个信标节点受到影响).首先固定漂移信标节点的数量，改变普通节点密度，当网络节点密度提高时，2种算法的检测准确率都相应提高，误检率相应降低，如图15所示.这是各节点可参考的邻居节点数量增加引起的.但UNDA具有更好的检测性能，这是因为UNDA的节点间接信誉推荐信任度更新机制，可以更好地排除漂移节点对其他节点判断准确性的影响，而NDD算法每一轮的检测都是一个全新的算法执行过程，检测性能不会因为时间的累积而提高.

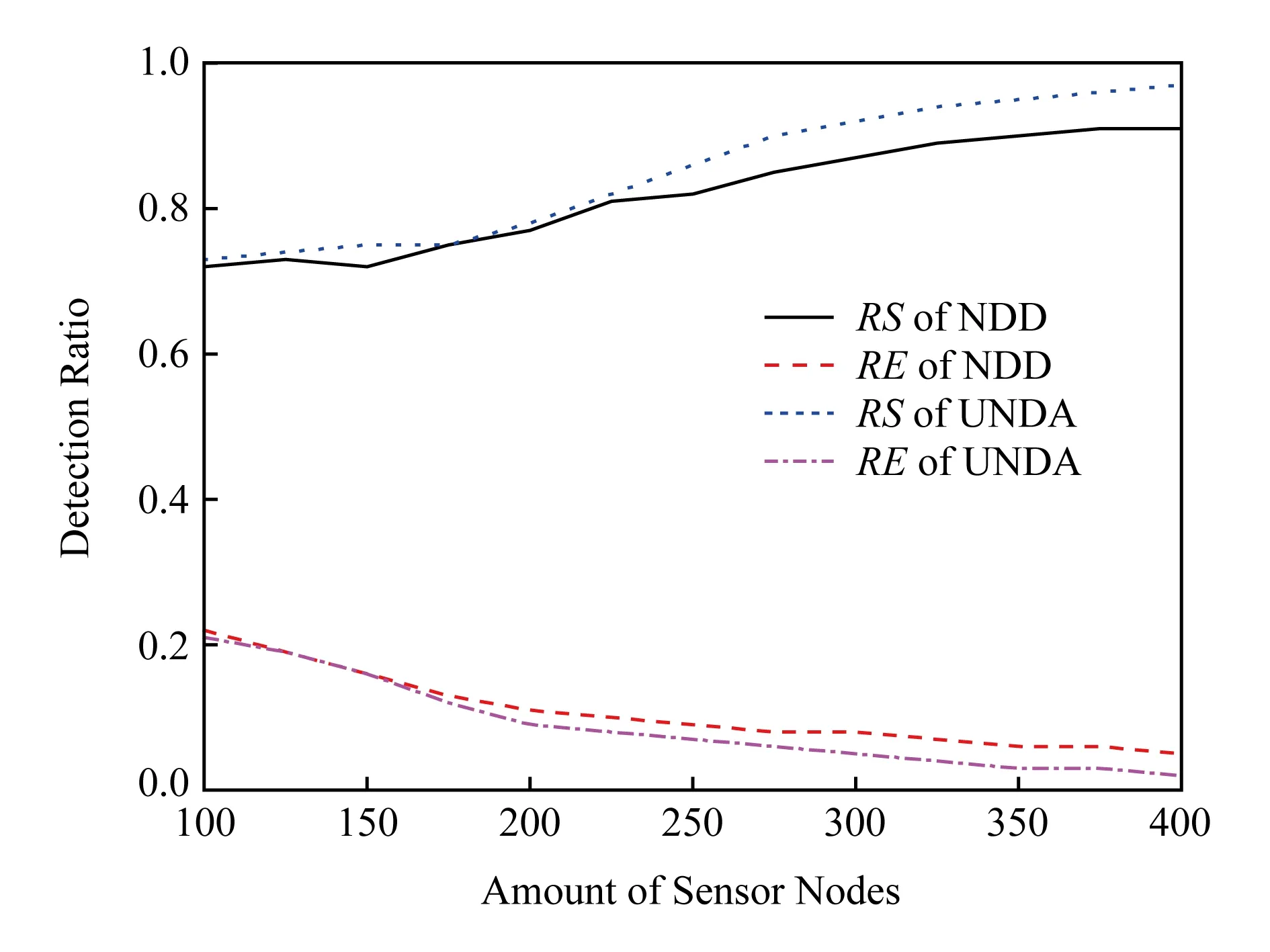
Fig. 15 Node density vs. detection performance图15 节点密度改变下的检测性能

图16展示的是固定节点数(300个)的情况下，共80个信标节点，位置不可靠的信标数量范围[4,40]步长为8，其中恶意信标占比50%，同样数量的虫洞场景下的算法性能比较.随着漂移信标的增加2种算法的性能都有下降，但相比之下，UNDA在漂移信标较多时，具有更高的检测成功率和较低的误检率，这同样是因为UNDA采用了间接信誉推荐可信度更新机制.

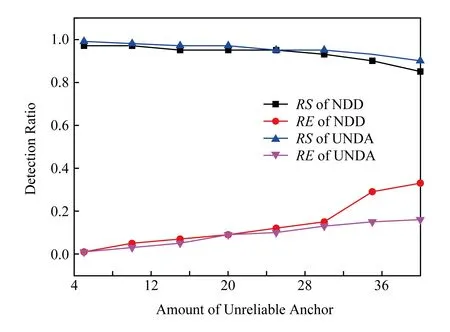
Fig. 16 Amount of unreliable vs. detection performance图16 不可信信标数量改变下的检测性能

而NLVF用于非测距的定位技术中因缺少类似工作，我们将文献[24]的投票依据由测距值替换为本文的分级跳距方法以移植到非测距定位场景，并简称为RF-NDD(rank feed-NDD)算法，由于非测距定位算法应用场景中信标节点通常较少，我们固定其数量为20个，其中8个信标发生漂移，2个信标受虫洞影响(2个虚假信标)，普通节点数量变化范围为[200,400],步长50，RSSI测量噪音为10%.

Fig. 17 Performance of NLVF in range-free scenario with variation of node amount图17 NLVF在非测距场景中节点数量变化时的性能

实验结果如图17所示，与基于测距的场景相似，由于缺少相互观测的积累和投票可信性的更新，节点密度变大时，RF-NDD性能并无明显的提升，而NLVF不但具有较好的检测性能，且随着节点密度升高，其性能也有显著提升，这对于节点密度较高的大型WSN来讲，具有实用性.设置RSSI噪音为20%和40%的2种情况以验证NLVF的鲁棒性.实验中共设置20个信标节点，网络平均连通度在[6,10]范围内变化，步长为1，20个信标节点全部成为不可信的信标，由于信标数量较少，故仿真结果采用节点个数代替比率，即检测成功的信标个数(number of detected anchor, NoD)和假阳性节点个数(number of false positive, NoFP).实验结果如图18所示，当RSSI噪音较大时，引起跳数等级划分不够准确，使得直接信誉值计算误差增大，但性能仍旧在可以接受的范围内，当网络平均连通度为10时，40%的RSSI噪音情况下，成功检测出18个不可信的信标，漏检2个；由假阳性引起的误检个数为3.在20%的RSSI噪音时，网络连通度达到9的情况下，误检率降为0，只漏检了1个信标节点.由于WSN的节点部署冗余特性以及节点较大的通信半径，平均网络连通度达到9的假设是切合实际的.

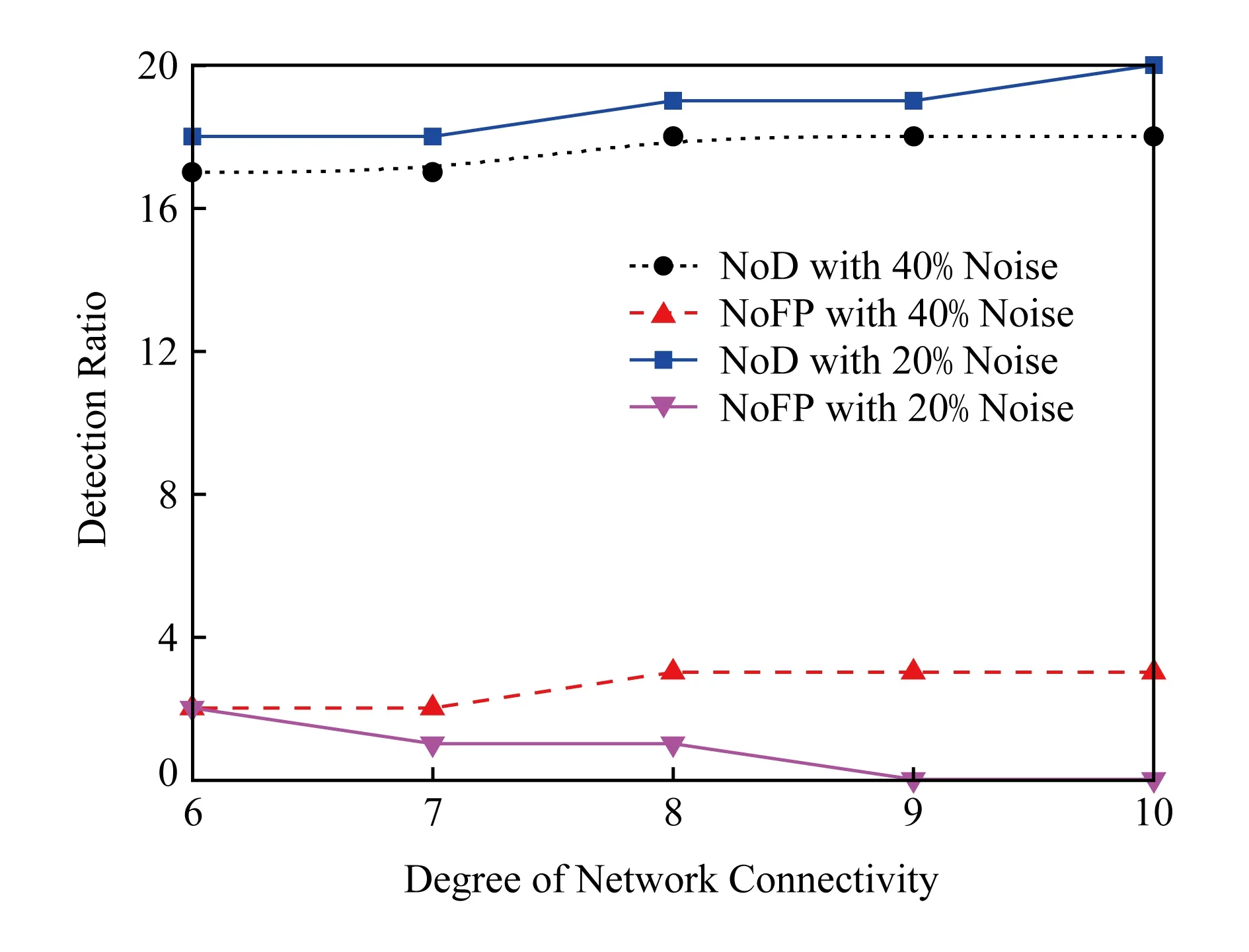
Fig. 18 Performance of NLVF in range-free scenario with variation of anchor amount图18 NLVF在非测距技术场景下的性能

6 总结与展望

本文提出NLVF框架，服务于基于测距的定位算法和非测距定位算法，用以过滤位置不可靠的信标节点，NLVF的核心算法UNDA以节点间的相互位置观测为基础，构建节点位置信誉模型，引入的间接信誉可信性更新机制，确保了算法收敛至稳定的判断结果.实验证明NLVF具有较高的检测率和较低的误检率，且具备轻量级的特点，适用于WSN.未来的工作将围绕临时信标选择算法展开，以解决信标过滤后的后果定位过程中可用信标不足问题，进一步完善NLVF的服务能力，并通过实物实验床验证NLVF的扩展性和重定位性能.