面向机器人抓取过程中目标位姿估计方法*
2019-06-25李树春刘满禄杨厚易刘理想
李树春, 张 静,2, 张 华, 刘满禄,2, 杨厚易, 刘理想
(1.西南科技大学 信息工程学院,四川 绵阳 621000;2.中国科学技术大学 信息科学技术学院,安徽 合肥 230026)
0 引 言
视觉引导机械臂进行抓取任务是目前机械臂抓取的主要方式。抓取过程分为目标识别、目标位姿估计和机械臂抓取。其中,目标位姿估计精度决定了抓取的效果。Lin C等人[1]采用双目视觉,通过双目立体视觉算法,对目标进行位姿估计,并采用快速特征点提取和描述(oriented FAST and rotated BRIEF,ORB)算法动态查找遮挡。随着Xtion[2],Kinect等廉价传感器的出现,大量研究者开始采用深度信息进行目标位姿估计。吕强等人[3]将RGB图像和深度图像结合,利用RGB图像提取(normal aligned radial feature,NARF)和尺度不变特征变换(scale-invariant feature transform,SIFT)特征点,采用随机采样一致性(random sample consensus,RANSAC)算法进行位姿估计。杨邱滟等人[4]利用Kinect相机对仿人机器人抓取进行目标定位。Besl P J等人[5]利用迭代最近点(iterative closest point,ICP)算法对刚性物体进行位姿估计,但是该方法在有遮挡的情况下会存在局部最小解问题。Lu J等人[6]提出了一种基于正态分布变换(normal distribution transform,NDT)算法的变尺度体素位姿估计法。
针对非结构化环境,本文使用深度相机Kinect获取点云图像,提取快速点特征直方图(fast point feature histograms,FPFH)描述子,结合奇异值分解算法和随机采样一致算法来对位姿进行估计。
1 机器人抓取系统
系统硬件平台如图1,由Microsoft Kinect深度相机,6自由度的轻量级机器人KINOVA MICO2和上位机组成。

图1 系统硬件平台
系统工作流程如图2,离线制作模板。
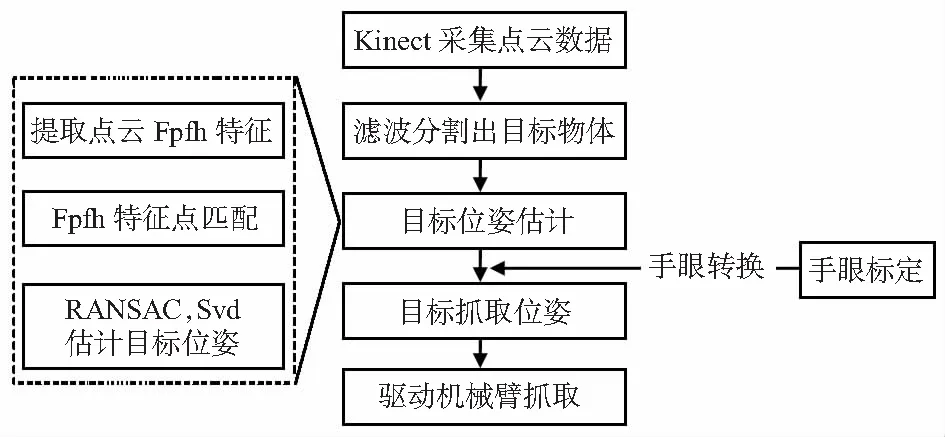
图2 系统工作流程
2 目标位姿估计
在对目标进行位姿估计前,先对场景进行体素滤波减少运算量,然后采用分割算法将目标与场景分割。
2.1 FPFH特征点提取
PFH描述符[7]通过考虑基于k领域中的点与其估计的表面法线之间的关系,来尽可能多地捕获点云的表面变化,适应邻域中存在不同采样密度或噪声水平[8]。
点云空间中的一对点pt和ps,如图3。
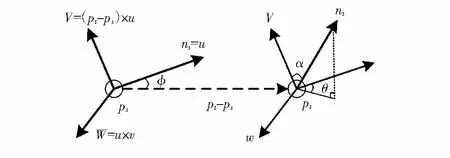
图3 点云空间中的一对点
FPFH描述子是在PFH基础上提出的,相对PFH描述子,FPFH的总体复杂度大大降低,且能保存PFH的大多数信息。FPFH描述子将α,φ,θ分别划分为11个区间,每11个区间的概率和为100 %,33 个区间概率总和为 300 %,如图4。
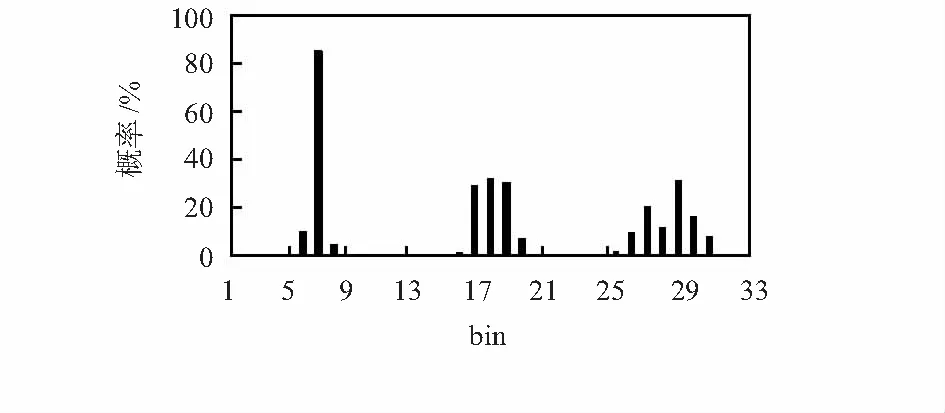
图4 点特征直方图
FPFH算法流程:
步骤1:对于每个查询点pq,计算出该待求点与其所有邻域点之间的相对关系,记作SPFH(pq);
步骤2:重新确定每个点k邻域,并通过 SPFH特征,来估计 FPFH特征,如下式所示
(1)
式中wk为第K个邻域点SPFH 特征的加权值。1/wk为pq与其第K个邻域点的距离值,用于表示点对(pq,pk)的关系。
2.2 旋转位移矩阵求取
在Rd空间中有两个点集P={P1,P2,…,Pn}和Q={q1,q2,…,qn},要找到这两个点集之间的旋转位移矩阵,可以把旋转位移用R和T表示
(2)
计算旋转位移矩阵的步骤:
步骤1:计算两个点集的重心
(3)
步骤2: 计算两个点集中每一个点减去重心后的偏移向量
xi=pi-,yi=qi-,i=1,2…,n
(4)
步骤3:计算X和Y的协方差矩阵
S=XTY
(5)
式中X和Y由向量xi,yi构成。
步骤4:对S进行奇异值分解,根据性质可得旋转矩阵
S=U∑VT
(6)
R=VUT
(7)
步骤5:由旋转矩阵可得位移
t=-R
(8)
2.3 RANSAC算法
RANSAC算法是一种通过对观测数据进行随机采样来估计模型参数的学习方法。给定一个数据集,其数据元素包含正确数据(inliers)和异常数据(outliers),RANSAC使用投票方案来寻找最佳拟合结果。
算法:RANSAC(P,Q)
Input:P,Q
Output:Rtfinal
Paranms:k,d,inlier
1:fori←1 tokdo ∥k为采样次数
2014年,在全国留学工作会议上习近平重点指出:“留学工作要适应国家发展大势与党和国家工作大局……培养造就更多优秀人才,努力开创留学工作新局面。”习近平这番话也为接下来的“一带一路”背景下高校来华留学生教育工作指明了方向。目前在“一带一路”背景下,我国高校为加强来华留学生教育采取很多有效教育措施,具体措施主要如下。
2:{p1,p2,p3}=Random(P)
3:{q1,q2,q3}=Fpfh{q1,q2,q3}
4:Ifd{p1,p2,p3}/d{q1,q2,q3}>d
Then∥由3个点构成的三角形边长比,d为比的最大阈值
5:Rt=Rt{p1,p2,p3,q1,q2,q3}
∥利用2.2节算法求解旋转位移矩阵
6:Q1=RP+t∥将初点云移动
7:Inlier=Euclidean(Q1,Q)
∥以两点云集的欧式距离作为得分
8:Rtfinal←inliermin(Rt)
∥将得分最低的旋转位移矩阵作为所得
3 实验与结果分析
3.1 杂乱无遮挡环境实验
在无遮挡的环境中,首先对环境进行滤波处理,分割出目标物体,分别使用本文算法、NDT算法和ICP算法在相同的环境对同一物体进行位姿估计,物体以任意姿态放置,如图5。3种算法位姿估计误差如图6所示。

图5 目标物体任意姿态放置
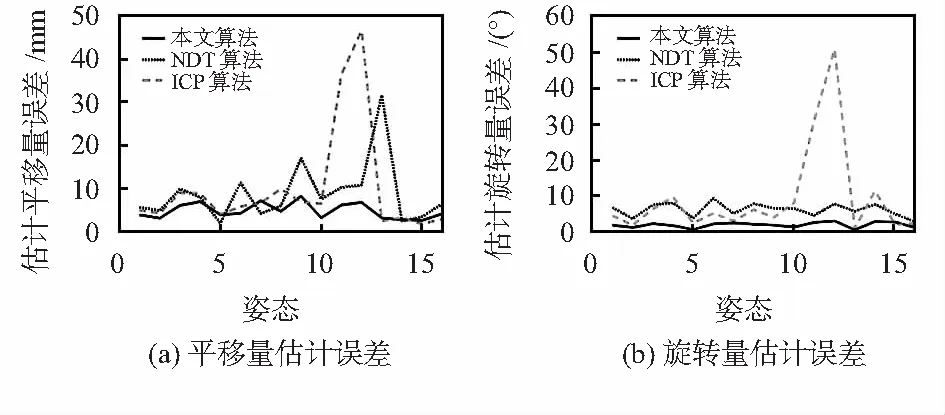
图6 3种算法位姿估计误差
由图6可以看出:在16种任意姿态下,NDT算法对旋转量的估计误差变化不大,但对平移量的误差估计出现了起伏。ICP算法对个别位姿会出现较大的偏差。针对任意姿态,经过多次实验,本文提出的算法位姿估计的平移量误差为4.86 mm,旋转量误差为1.96°;NDT算法的平移量误差为8.86 mm,旋转量误差为6.16°;ICP算法平移量误差为10.03 mm,旋转量误差为12.49°。
3.2 机械臂遮挡目标物体实验
针对Eye-to-Hand模型易出现机械臂遮挡目标物体的问题,本文设计了实验,机械臂在不同遮挡率下遮挡住物体,利用本文算法、NDT算法和ICP算法进行位姿的估计。实验结果如图7。
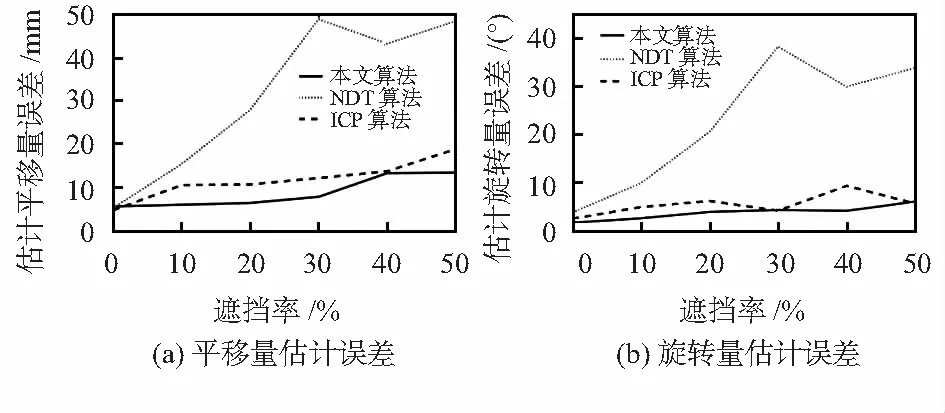
图7 不同遮挡率下的位姿估计误差
由图7可以看出:随着遮挡率的增高,3种算法对平移量和旋转量估计的误差都在增加。由于NDT算法利用概率分布来计算位姿并没有计算点云的特征,在遮挡导致物体信息缺失情况下对物体位姿估计的效果并不好。ICP算法通过欧氏距离来进行位姿估计,但同样缺失点云特征,在物体信息缺失时易出现偏差。本文提出的算法是利用点云的特征信息来进行位姿估计的,所含有的信息量丰富,即使部分信息缺失也能有效估计位姿。图8和图9是在10%遮挡率下3种算法对位姿估计的效果。其中图8中浅色的点云表示初始位姿,深色点云为彩色图像转换后的点云。图9中浅色点云是将初始点云经过估计的位姿移动后得到。可以看到本文初始点云经过旋转位移与移动后的点云基本重合。而NDT和ICP算法的重合效果较差。

图8 采集点云数据

图9 3种算法估计效果
4 结 论
通过与NDT算法和ICP算法进行对比实验,本文提出的算法在对位姿估计精度和稳定性上都优于NDT算法和ICP算法,并在Eye-to-Hand模型中机械臂存在遮挡物体问题上对位姿估计的效果也要优于其他两种算法。在后续的工作,可以在保持位姿估计的精度情况下,对算法的时间复杂度进行优化,使算法的实时性效果更优。
