减小金属筒形谐振子振型偏移角的方法

韦俊新, 史 炯, 丛 正

(天津航海仪器研究所，天津 300131)

0 引 言

金属筒形谐振陀螺是固体波动陀螺的一种，利用筒形谐振子被激励驻波的惯性效应实现陀螺在其敏感轴转角的测量，该类陀螺用振动元件代替了传统陀螺的机械转子，用微幅振动取代了高速旋转，具有结构强，能耗低，精度高等优点，在兼顾抗高过载、量程大方面表现了巨大的潜力[1]，同时也具有加工简单，陀螺制造难度低，易于批量化生产等优势，发展和应用前景极为广阔[2]。

目前在金属筒形陀螺及其谐振子振型偏移角的研究方面，国内外许多学者和研究机构已做过不少的工作。Innalabs公司在圆柱形金属谐振子的底部加工出轮辐状沟槽，通过减小谐振子的频率裂解以减小谐振子振型偏角[3]。Watson公司将压电电极镀于圆柱壳体的表面，并且将电极设计为分离的小片，可以实现左右的振型校正[4]。国内对于金属筒形谐振陀螺研究尚处于实验室样机阶段，尚未见工程化的应用，国防科技大学王旭、陶溢等学者在对谐振陀螺产生振型偏移角的原因及测量方法进行过研究，并从谐振子加工及修调上提出了减小振型偏移角的方法[5,6]。

本文理论分析了金属筒形谐振子振型偏移的影响因素，通过实验验证了振型偏移对谐振子振型对称性及正反转差异的影响。根据振型偏移下波节点输出电压方程，提出基于前馈调幅调相和基于调制解调反馈控制的两种不同的振型校正方法，并通过实验验证其校正效果。

1 金属筒形陀螺的基本原理

谐振子底面的压电电极施以与谐振子的固有频率同频的交流电压信号，由于压电陶瓷的逆压电效应，激励出谐振子的驱动模态(图1(b))，当角速度输入时，在哥氏力的作用下敏感出与驱动模态振型相差的敏感模态[7](图1(c))，压电电极的正压电效应检测敏感模态的振幅，经过外围解调线路解算出角速度大小。

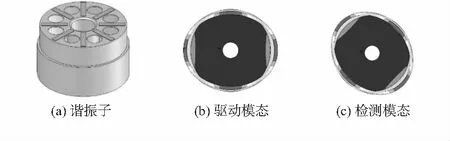
图1 金属筒形陀螺核心部件及工作模态

2 振型偏移角的产生原因及影响

谐振子材料的不均匀性和加工误差等因素，会引起谐振子的频率裂解和阻尼不均匀[2]，因此谐振子存在刚性轴与阻尼轴[6]，频率裂解、阻尼不均匀、刚性轴和阻尼轴与激励轴之间的夹角等因素均引起谐振子的振型偏移角[8]。

2.1 谐振子的频率裂解

存在频率裂解情况下，谐振子振型偏移角可以由公式(1)表示[9]

(1)

式中ω0为谐振子的谐振频率，ΦL-ΦH为两个刚性轴之间夹角，Δω为频率裂解，φ0为刚性轴的方位角。

由式(1)表明，频率裂解引起的振型偏移角的偏移速率大小与频率裂解以及刚性轴与主振型轴之间的方位夹角8倍正弦值成正比。

设刚性轴方位角为定值，当频率裂解为0.1,0.5,0.01 Hz时，其振型角度漂移如图2。

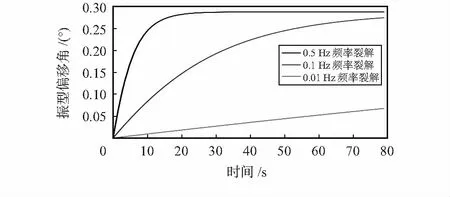
图2 频率裂解导致的振型偏移随时间的变化

如图2所示，频率裂解越大，振型偏移角也越大，且振型偏移角随时间逐渐增大，最终达到稳定。

2.2 谐振子的阻尼不均

阻尼不均匀引起的振型偏移，如式(2)可得

(2)

式中ξ0为均匀的阻尼，γ4为阻尼的不均匀程度，φ0为衰减常数最小阻尼轴方位角。

式(2)表明，金属筒形陀螺振型偏移角与谐振子阻尼不均匀程度及小阻尼轴与主振型轴之间的方位夹角4倍余弦值成正比。

假设阻尼轴方位角22.5°，当阻尼不均匀为0.01，0.1，0.3时，其振型角度漂移如图3。

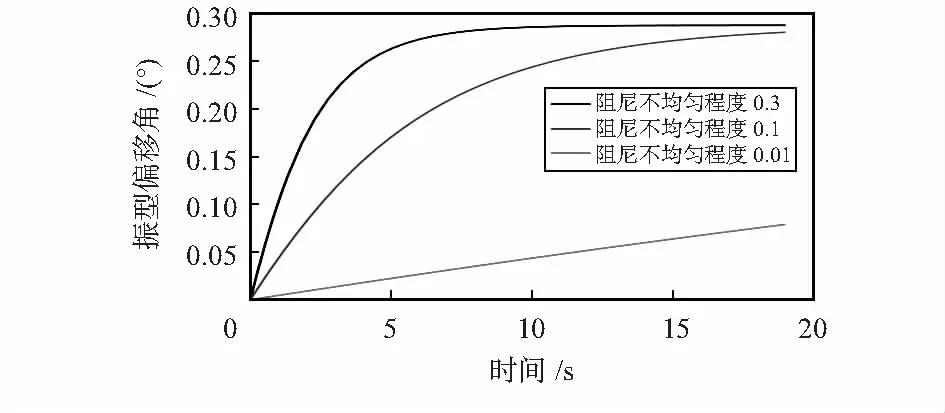
图3 阻尼不均匀导致的振型的偏移

由图3可知，阻尼不均匀程度越大，最终振型的偏移速率越大；且振型的偏移量随时间增大，最终趋于稳定。

2.3 振型偏移角对陀螺性能的影响

选择实验室现有的金属筒形及配套的驱动线路用于测试谐振子振型偏移的程度，用以分析振型偏移造成的影响，谐振子的参数：谐振频率为5.4 kHz，品质因数Q为7 000，频率裂解为0.52 Hz。

驱动线路板对置于转台的谐振子施加正弦激励使其达到驱动模态并且使谐振子波腹点振幅保持稳定，转台以10″/s2的加速度沿顺时针方向转动至10°/s速率，采集节点电压信号；同样，转台以相同加速度沿逆时针方向转动至10°/s速率，采集节点电压信号。结果如图4所示。

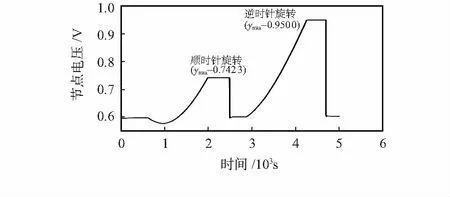
图4 存在角度偏移条件下顺逆时针旋转节点电压输出

由图4可知：1)顺时针旋转转台时，节点电压存在先降后升的趋势，说明该方向旋转时，45°处压电电极处的振动经历了先减弱后加强的趋势，而逆时针旋转无此现象；2)顺逆旋转最终角速率均为10°/s，但节点电压输出大小不同，逆时针旋转时节点电压输出比顺时针旋转节点电压大近210 mV。

本文利用德国Polytec公司的PSV—400型多普勒激光测振仪对金属谐振子唇沿部分的径向振幅进行测量。谐振子环向测试点数400，得到的振幅数据如图5所示。

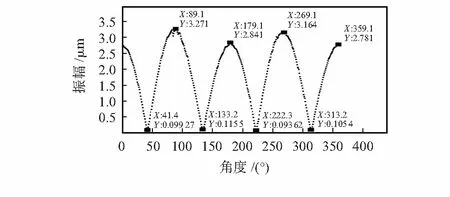
图5 谐振子环向振幅数据

由图5可知，谐振子波腹点与波节点振幅及所处角度如表1、表2所示。

表1 波节点振幅及所处角度

表2 波腹点振幅及所处角度

由图4、图5和表2可以看出：谐振子4个波腹点的振幅大小并不一致，最大相差0.43 μm，说明振型有畸变，同时驻波振型节点偏离节点检测压电电极所在位置。

3 振型校正方法

校正谐振子振型的方法，从谐振子方面主要是提高加工制造精度、降低材料的不均匀性，采用更合适的修调方案，比如去质量修调方案[10]等，降低谐振子的频率裂解，本文从线路角度，提出两种振型校正方法，以进一步减小振型偏移。

3.1 前馈调轴法

受到激发的谐振子会产生四波腹振动，其环向振型为

Uo(t)=Acos 2(θ-α)sin(ωpt+β)

(3)

式中ωp为谐振子的谐振频率，α为谐振子的振型偏移角，理想情况下α=0。

已知当两个同频率，同相位的外界激励力(F1，F2)同时作用于壳体的0°电极轴和45°电极轴时，相当于一个幅值为F3的外界激励力单独作用于壳体环向一点[11]。改变F1和F2的比值，就可以改变θ

U3=U1+U2=Ecos 2(θ-θE)cosωt

(4)

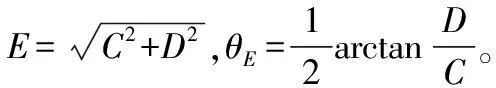
改变C和D幅值比值，就可以使壳体发生环向振型的移动，选取一个合适的比值，令α-θE=0，使壳体发生的进动抵消振型的偏移，进而消除偏移量。

因此，在谐振子选取一点施加一定幅值激励信号，通过调节此激励信号的幅值和相位，纠正谐振子振型的偏移误差，图6是线路控制方案。

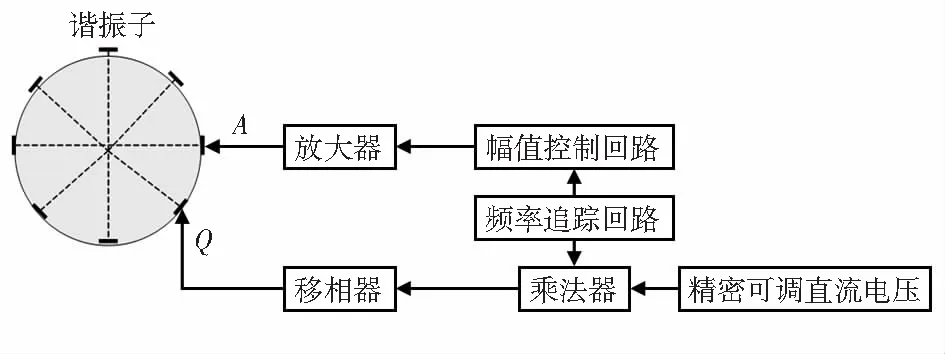
图6 前馈调振型轴线路控制方案

该方案可较为彻底的对振型进行调整，但同时仍存在问题：由前文所述，频率裂解和阻尼不均匀引起的谐振子振型的偏移随时间而变化，前馈调轴法无法随时感测谐振子振型角度的改变，以自动调整施加校正电压Q的幅值和相位，不利于金属筒形陀螺在工程上的应用。

3.2 反馈调轴法

反馈调轴法是通过解调表头输出信号q，分解其同相和正交分量，分别进行控制后通过调制合成为反馈控制信号，以抑制谐振子振型的偏移。其线路控制基本示意如图7所示。

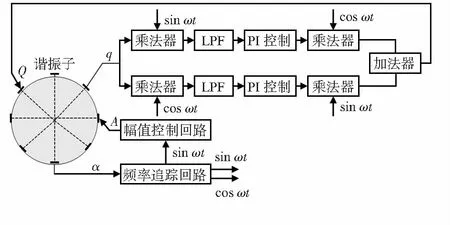
图7 反馈调振型轴线路控制方案

检测端输出的振动信号V可以表示为[12]

V=KΩZsin(ωt+φsense)+VKsin(ωt+φq)+

VIsin(ωt+φsense)

(5)

式中KΩZsin(ωt+φsense)为角速度耦合信号，VKsin(ωt+φq)是正交误差信号，VIsin(ωt+φsense)是同相误差信号。

当无角速度输入时即ΩZ=0，则此时振动信号可以表示为

V=VKsin(ωt+φq)+VIsin(ωt+φsense)

(6)

通过sinωt和cosωt解调和滤波，可得

I=VKsinφq+VIsinφsense

(7)

K=-VKcosφq-VIcosφsense

(8)

通过sinωt和cosωt调制和相加，可得驱动信号Q

Vdrive=-VKcos(ωt+φq)-VIcos(ωt+φsense)

(9)

该驱动信号反映到测量点节点电压处时，可得

(10)

该信号可有效消除原节点电压信号V，即消除了振型的偏移角。

所提方案的优点是能即时的感知振型偏移造成的节点电压的变化，通过反馈回路消除振型偏移角，弥补前馈调轴方案的不足，提升了在陀螺工程化应用价值。但所提方案不足之处在于，由于对谐振子加工，装配误差等因素，正交误差信号与同相误差信号可能会附加误差项，故对振型的调整并不能很彻底。

4 试验验证

采用图6所示的流程图设计了前馈调轴板，并进行了实验，结果如图8(a)所示。

同样，利用激光测振仪对调轴后的谐振子唇沿振型进行了测量，得到环向振幅与振型分布，如图8(b)所示。

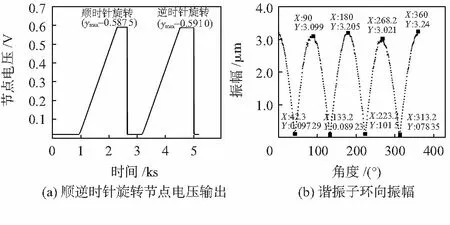
图8 前馈调轴后实验结果

由图8(b)可知，谐振子波腹点与波节点振幅及所处角度如表3、表4所示。

表3 波节点振幅及所处角度

表4 波腹点振幅及所处角度

通过前馈调轴之后，对比表2和表4；表3和表5可见：1)谐振子振型相对调轴之前偏移了0.8°～0.9°；2)改善了振型4个波腹振幅不一致的问题，4个波腹点振幅最大相差0.219 μm，比调轴前的差值减小了近50 %；3)节点电压的振幅明显降低。说明前馈调轴方案能够有效地减小谐振子振型以及振幅的偏移。

采用图7设计了反馈调轴板，实验测试调轴效果如图9(a)所示，其振型分布图如图9(b)。

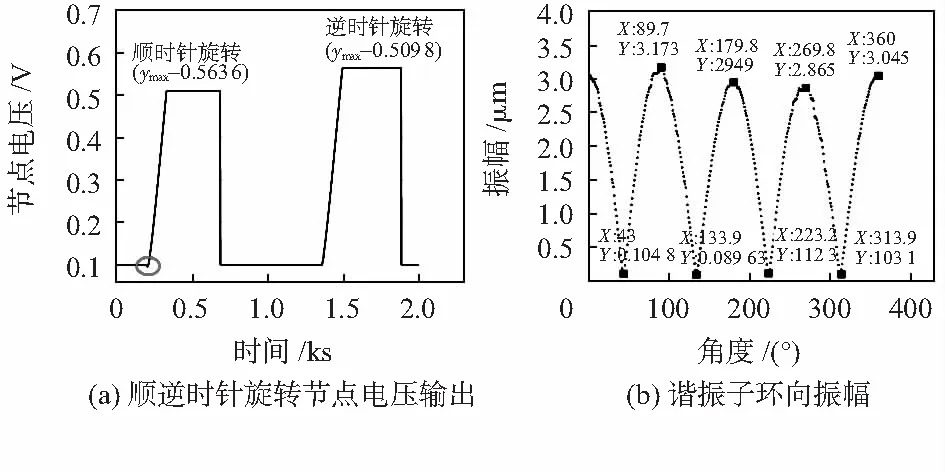
图9 反馈调轴后实验结果

由图9(b)可知，谐振子波腹点与波节点振幅及所处角度如表5、表6所示。

表5 波节点振幅及所处角度

表6 波腹点振幅及所处角度

通过反馈调轴之后，与调轴之前相比，可得：1)从波腹和波节所处的角度可知谐振子振型相对调轴之前移了0.6°～0.7°；2)振型四个波腹点振幅相差最大值是0.308 μm，与调轴前相比已有所减少；3)由图10可知，顺时针旋转时依然存在先下降后上升的现象，但相比调轴前已经减弱很多。

经实验验证，前馈调轴及反馈调轴均能改善振型偏移的问题，但是反馈调轴效果弱于前馈调轴的效果。

5 结 论

本文分析了金属筒形谐振子振型偏移的原因，利用实验验证了谐振子振型偏移造成的影响，并从线路控制方面提出了两种解决振型偏移的方案，通过实验验证，该两种方案能够有效地校正振型偏移，进而减小振型偏移的造成的影响，并分析了两种方案的优缺点，为后续对金属筒形谐振陀螺研究奠定了基础。