电涡流测厚系统特征值提取方法*
2019-06-25王志春丁东阳
燕 芳, 王志春, 丁东阳
(内蒙古科技大学 信息工程学院,内蒙古 包头 014010)
0 引 言
常见的无损检测方法有射线法、超声波法、电涡流检测法等。射线法在检测过程中存在较大的安全隐患,若防护不得当则容易对检测人员的身体造成伤害;超声波检测则需要大量耦合剂,且检测精度相对较低;利用电涡流检测[1]方法可以实现金属板的相关厚度无损测量,例如对金属表面的油漆厚度、覆盖绝缘层厚度及金属试件等厚度检测[2~9]。电涡流检测方法尤其适用于被测金属试件处于高速旋转或高温环境等一些不便进行直接测厚的情况。
1 电涡流检测技术
脉冲涡流检测技术[10,11]是以法拉第电磁感应定律为理论基础的。被测金属试件处在感应磁场时,当金属试件切割磁力线,或磁场强度发生变化时都会造成通过金属试件的磁通量发生改变,从而在被测金属试件内部产生感应电动势。进而生成脉冲感应电流,由感应电流生成的脉冲感应涡流磁场如图1所示。
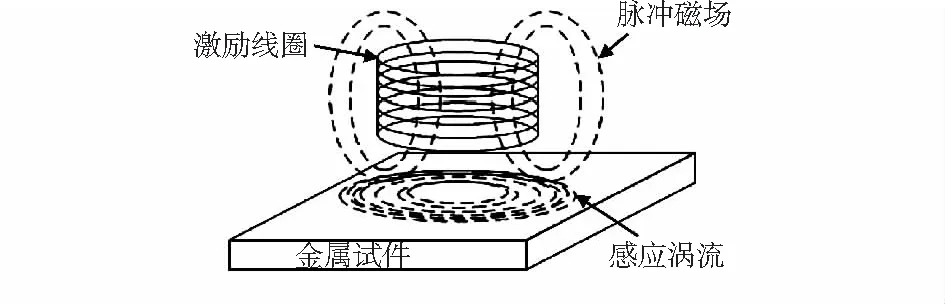
图1 脉冲感应涡流磁场示意
2 系统仿真与结果分析
2.1 基于Maxwell 的3D的仿真模型
基于Maxwell 建立的3D仿真模型如图2所示。磁芯为半径8 mm,高度26 mm的带铁芯圆形骨架结构。线圈的内、外半径分别是10 mm和12 mm。下面的灰色平板表示0.1~0.4 mm的铝板,模型的提离距离设定为6 mm,则它的求解域体积是模型体积18倍。
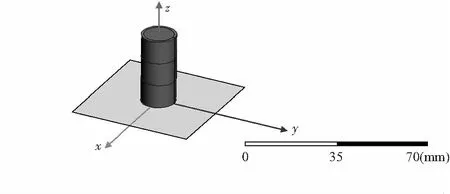
图2 线圈与被测体的3D仿真模型
2.2 仿真结果与分析
仿真实验数据如表1所示,从表1中数据可以看出:感应电压峰值与过零点时间都是随着被测铝板厚度的增大而增大,由此可见,可以选用电压峰值与过零点时间作为特征值,建立特征值与被测铝板厚度之间的关系。
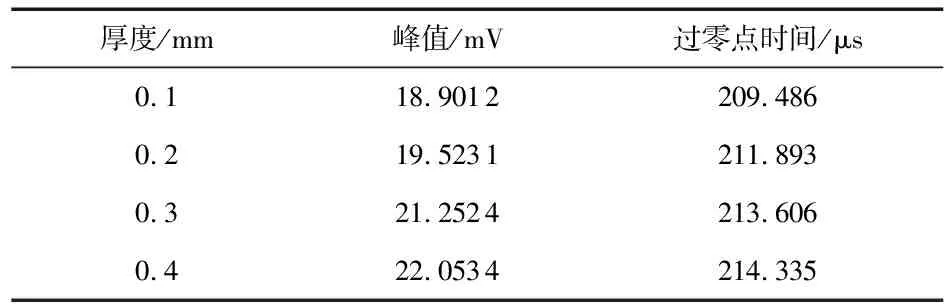
表1 仿真实验数据表
被测铝板厚度与感应电压峰值对应关系如图3(a)所示曲线,可见,铝板厚度从0.1~0.4 mm变化时,对应的感应电压峰值也在逐渐变大。被测铝板厚度与过零时间点的对应关系如图3(b)所示曲线,可见,被测铝板厚度从0.1 mm变化至0.4 mm时,对应的过零时间也在逐渐变大。
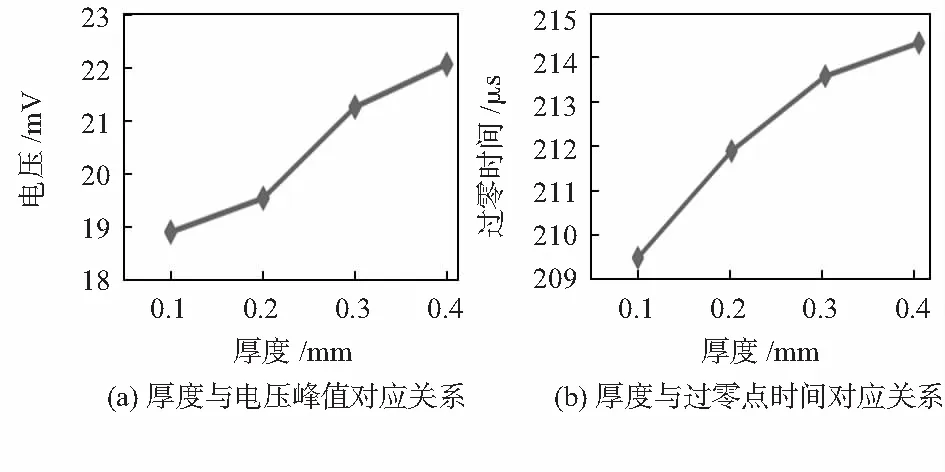
图3 仿真结果
根据图3(a),被测铝板厚度与电压峰值之间对应关系可拟合出公式(1),根据图3(b),被测铝板厚度与过零点时间之间对应关系可拟合出公式(2)
ρ=21.441 7Δ2-0.213 5Δ+18.708 2
(1)
(2)
3 电涡流测厚系统总体设计方案
基于STM32的电涡流测厚系统的总体设计方案如图4所示,首先,通过STM32F103单片机的输入/输出(input/output,I/O)口发出脉冲激励信号脉宽调制(pulse width modulation,PWM),作为通入传感器线圈的激励信号,使传感器线圈的激励端产生脉冲磁场,该脉冲磁场作用于被测铝板使其感生出一个变化的磁场,其次,传感器线圈的检测端也会感应到这个变化的磁场。最后,利用CS5521采集传感器线圈检测端与参考端的差分信号,将采集的数据全部存储在单片机中,有单片机进行相应的数据处理,处理后的结果在TFTLCD显示屏上进行显示。
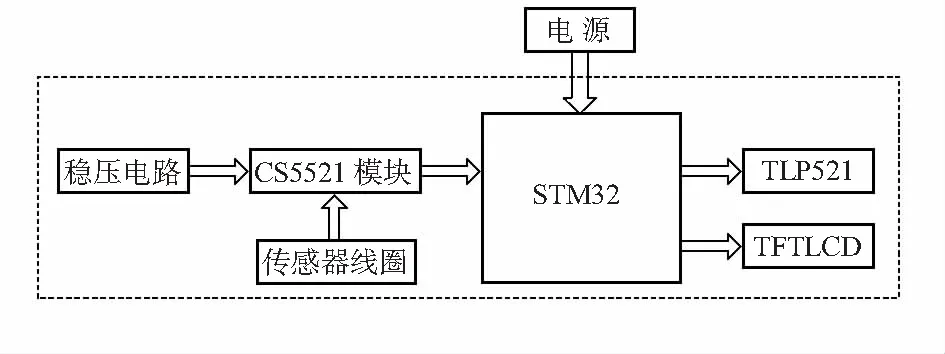
图4 系统总体设计方案
4 实验结果分析
本次实验在常温情况下对厚度为0.2~1.0 mm的铝板进行了检测,首先将各个模块用杜邦线按对应引脚连接起来,然后将程序下载到STM32开发板中,当系统处于稳定状态后,开始进行实验,同时记录实验数据,如表2所示。

表2 实验数据表
通过单片机的串口输出存储在中的3 000个数值,将这些数据导入到Excel表格中,通过降序排序的方法找出这些数中的最大值,然后与单片机处理后的电压峰值进行比较,发现两个数值相等,这说明单片机处理的数据结果是准确的。通过实验检测0.2~1.0 mm的铝板厚度与峰值电压的拟合曲线图如图5(a)所示。
将每次实验求出的10次过零点时间取平均值后作为这一厚度对应的过零点时间,通过实验检测0.2~1.0 mm厚度的铝板得出了过零点时间与铝板厚度的对应关系,0.2~1.0 mm铝板厚度与过零时间的拟合曲线图如图5(b)所示。

图5 实验结果
根据表2中厚度、电压峰值、过零时间的实验数据在MATLAB中拟合出3个量之间的曲面图如图6所示。
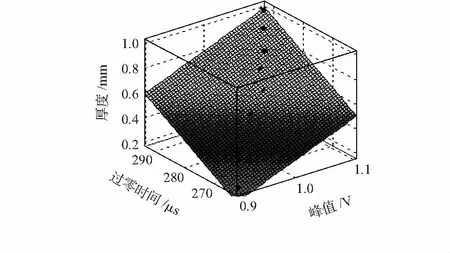
图6 厚度、电压峰值、过零时间之间的三维图
最后通过实验获得快速傅里叶变换(fast Fourier transform,FFT)运算后的数据结果,就能计算需要求解的谐波幅值。在数组lBufMagArray中存储谐波的幅值。通过单片机的串口把lBufMagArray数组中各次谐波的幅值数据输出来,获得到需要的幅值特征量。在实验中检测0.2~1.0 mm的被测铝板厚度与幅值之间的拟合曲线如图7所示。
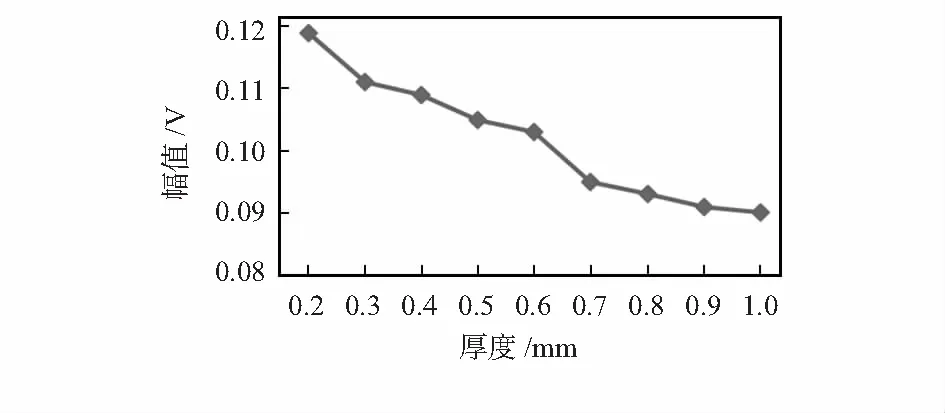
图7 厚度与幅值的对应关系
通过上述3条拟合曲线可知:当铝板厚度从0.2~1.0 mm变化时,检测到的感应电压峰值与过零点时间均是随着被测铝板厚度的增大而增大的,而幅值则随着被测铝板厚度的增大而不断变小,由此可见,此结果与之前的仿真实验结果相吻合。再一次说明如果选用电压峰值、过零点时间和幅值这3个量作为特征值,建立这三个特征值与被测铝板厚度的关系,即可达到最终反演厚度信息的目的。
本文采用了1个二阶非线性模型,通过在给定激励频率情况下检测信号的变化值与被测铝板厚度之间的对应关系来拟合对应的关系曲线。设定被测铝板的厚度值大小是γ,二阶多项式最终拟合的函数如下
(3)
式中γ为铝板厚度,U为电压峰值,φ为过零点时间,B为幅值,aij(i=1,2,3;j=1,2,3)为相应的关系参量。把表2中的实验数据代入式(3)中得出
γ=0.009 0U+0.009 0φ+10.018 1B-0.963 7
(4)
5 误差分析
实验测得的铝板厚度与实际厚度之间存在误差,经查阅相关资料及综合分析,引起测量误差的原因可能有以下3个方面:1)实验环境中有噪声和其他信号的干扰;2)被测铝板的表面不平整;3)传感器线圈的检测精度不高。
因此,在后续实验中应尽量减少实验环境噪声,还可以通过改良优化线圈以及对采样信号进行滤波处理的等方法来减小测量误差。
6 结束语
此电涡流测厚系统中还有很多环节需要改进和完善,如检测系统中检测精度还需要更进一步提升。另外还需要提取更多的特征值进行测试,从而寻找到更多有关被测体参数的相关信息。后续的研究方向可以考虑将原始信号与检测信号共同进行快速傅里叶变换后再作差,通过分析不同厚度对应的临界值来确定金属体的厚度。
