改进遗传算法在共享单车停放点分配中的应用*

2019-06-25施嘉伟陈观林

传感器与微系统 2019年7期

施嘉伟，陈观林,，徐煌

(1.安徽理工大学计算机科学与工程学院，安徽淮南 232000；2.浙江大学城市学院计算机与计算科学学院，浙江杭州 310015)

0 引言

共享单车停车服务请求过多时存在着竞争关系，加上车辆与停放点之间的数量制约，处理请求的顺序不同使得分配效果会有所差异，造成总距离代价不同。在停放点分配问题中的优化目标不止一个，需要使用多目标优化算法[1]。而遗传算法本身属于随机搜索类算法，在实际应用中很容易陷入局部最优的情况，因此需要对其进行改进。

文献[4]提出了一种自适应量子旋转门更新方式改变了种群进化的方向，从而提高算法的全局搜索能力。文献[5]提出了一种融合贪心算法的遗传算法在仓储车辆调度优化中的应用，让交叉、变异用起来更加灵活，有效的提升了算法的调度效率。文献[6]在传统的滑膜控制方法加入了神经网络，利用Lyapunov函数推导了神经网络权值的自适应律，提高了原方法一定的精度。文献[7]提出了一种新的智能停车系统原型，采用遗传算法解决了停车场车辆调度问题。文献[8]目标是使加权流量和库存成本之和最小化，为了有效地求解该模型，开发出基于遗传算法的启发式算法。

线性回归是机器学习中经典的回归算法，是现在主要的统计预测技术[9]。融合了线性回归的遗传算法可以找出停车顺序中的内在联系，将遗传算法生成的新个体用作线性回归的训练集，对训练后的回归系数排序，预测出停车的优先级，能够改善遗传算法局部搜索能力较差的缺点。因此，使用线性回归对遗传算法产生的个体进行训练，能够得出一个有效的停放点分配方案。

1 数学模型

本文主要解决共享单车停放点分配问题。共享单车乱停乱放一直是行业诟病，现如今逐渐建立起了智能停放点和电子栏杆等约束停车的方案。停车诱导系统的研究是该行业未来发展的方向，因此停放点分配问题需要制定良好的模型。本文采用双目标遗传算法建模，设f(x)为待停的单车到停放点的距离代价总和，g(x)为所有停放点之间的停车密度代价总和。数学模型可表示为

(1)

约束条件如下

2 多目标遗传算法的实现

优化问题通常有多个优化目标，各个目标之间又是矛盾的，因此要使所有子目标同时达到性能最优是不可能的。通常多目标优化问题的解是由一组Pareto最优解集构成的，其中每一个元素都成为非支配解。

2.1 染色体编码与初始化种群

本文采用自然数对每辆车进行编码，自然数编码因带有实际意义而有着广泛的应用。停车的顺序会对最终求得的距离代价产生影响，按处理停车的时间先后顺序组成多目标遗传算法中的染色体。

初始化种群操作为随机生成染色体中每个基因的排列，将基因排列随机打乱如下

式中x为染色体,x1,x2,…,xn为车辆的编号随机排序。例如，染色体[4,2,1,3]为4#车先停，2#车其次，以此类推。

2.2 快速非支配排序和拥挤度计算

多目标遗传算法无法实现多个子目标同时达到最优，因此要使用快速非支配排序和拥挤度对种群进行筛选，作为衡量种群优劣的指标。

快速非支配排序：首先找出种群中的非支配解，记为第一梯度并标记为1，然后从种群中剔除这一梯度的解；继续找出剩下个体中的非支配解，记为第二梯度并标记为2，以此类推，对种群中所有个体标记，同一层的个体拥有相同的标记值。

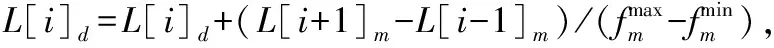
2.3 适应度函数与解码

在停放点分配问题中，距离代价主要由停车的顺序和可用停放点决定，由于引入了可用停放点的条件，后停的车辆在不同的染色体中会被分配到不同的停放点。距离代价的解码过程用贪心算法进行求解，统计待停车辆到可用停放点的总距离。

密度代价主要由各停放点的车辆密度组成，使用均方差进行计算。引入密度代价使管理更加方便。

2.4 选择和交叉算子

本文选择锦标赛选择算法。由于该算法执行的效率高以及实现简单的特点，锦标赛选择算法是很流行的选择策略。在当前子代种群中抽取若干对染色体，选择快速非支配排序和拥挤度较优的个体作为精英保留到下一代。操作如下：1)确定每次选择的个体数量(本文选择2个)；2)在种群里随机选择个体，两两构成一组，根据快速非支配排序和拥挤度，选择适应度最好的个体作为竞争胜利者；3)重复上一步骤，得到足够的个体构成新一代种群。

染色体中车辆的序号唯一，造成染色体中不能出现重复的序号，随机选择自身某段的基因进行自交。

2.5 精英策略

在多目标遗传算法中加入精英策略可以保证基因良好的个体遗传到下一代，保持种群的多样性，同时也让种群的大小维持在一个固定的数量。

2.6 实验结果分析

Pareto最优解集如图1(a)所示。遗传算法的终止条件有多种，本文选择距离代价达到特定收敛阈值作为结束条件。经过实验可以发现，多目标遗传算法在经过一定的代数之后可以得到一个Pareto最优解集。在解集中用人工干预选择出适合当前问题的解。

从图1(b)可以看出，距离代价在子代个数达到5 000之后陷入了局部最优的情况。理论上距离代价会随着代数的增长而收敛，但需要花费的时间成本可能会随着决策变量的增加而大量增加，因此需要对其进一步优化。由于距离代价是优化的主要目标，接下来对这个单目标进行算法的改进。

图1 实验结果

3 融合了线性回归的改进遗传算法的实现

融合线性回归的遗传算法在基础的遗传算法框架上，融入了线性回归算法，将每辆车是否停到最优停放点作为输入，距离代价作为输出，训练出一种有向的染色体基因组成，改善了遗传算法的局部搜索能力。改进遗传算法流程图如图2所示。

图2 融合了线性回归的遗传算法流程

线性回归模型如下

Y=wx+b,x∈{0,1}

(2)

式中xi为车辆是否停到最近的停放点，取值为1或0。wi为线性回归系数，Y为停车的距离代价。编码如下

(3)

例如，上述第一行[1,0,0,1]，为1#车与4#车停到了最优停放点，2#车与3#车竞争资源失败，停到了次优停放点。

线性回归是一种普通的回归算法，但应用广泛。损失函数如下

(4)

对于这个损失函数，有两种求解最小值的方法，分别是梯度下降法和最小二乘法。因损失函数为平方损失函数，在此情况下，回归问题可以用最小二乘法解决。利用最小二乘法可以解出回归系数w=(XTX)-1XTY。训练结束后，将回归系数进行排序。训练之后的回归系数w=[w1,w2,…,wn]。

假设将回归系数升序排序后得到以下序列[w3,w2,w1,w4]。则最终预测出的停车优先级为[3,2,1,4]，该顺序表示当前训练结束后该车辆停到最优停放点对总距离代价的影响程度，影响较大的先停。

每产生一个新的子代，便将其加入线性回归的训练集，使遗传算法和线性回归同步进行。每次更新训练集后重新训练，将训练后得出的回归系数进行排序，获得新的染色体基因构成。单纯使用线性回归在此模型中并不具有稳定性，因此,将线性回归融入遗传算法稳定的结构中能更快地找到最优解。

实验结果会受到供需比的影响。每个停放点数量上限不同会导致停车的方案和适应度产生较大的差异，供需比在0.5以下会导致算法在短时间内快速收敛，此时并不需要加入线性回归来加快收敛，可以直接用贪心算法来解码。只有在供需比大于0.5时，算法在本文环境下才有实际的作用。供需比大于0.8的情况较少且单靠遗传算法的运算时间急速激增，最终决定把供需比调节在0.65～0.75之间。图4是供需比在0.75时的效果图。