极化SAR图像Pauli-Wishart非监督分类算法*

2019-06-25胡兆勇吴悦明陈和恩

传感器与微系统 2019年7期

朱腾, 胡兆勇,, 吴悦明, 陈和恩,

(1.广东工业大学机电工程学院，广东广州 510039; 2.广东工业大学广东省CIMS重点实验室，广东广州 510039)

0 引言

全极化合成孔径雷达SAR(polarimetric synthetic aperture radar，PolSAR )是主动遥感重要手段之一，由于在云、雪、雨、雾等恶劣自然条件下有良好的适应性而在农业、林地、军事等方面均有重要应用[2]。

影像分类是PolSAR数据的关键应用之一，为了有效地利用PolSAR影像中隐含的回波信息，近十几年来研究人员提出的分类方法大多以基于目标散射机理的方法为主[3]，如基于相干目标分解的Pauli分解、Krogager分解[4,5]，基于非相干目标分解的Kennaugh分解、Cloude-Pottier分解、Freeman分解[6～9]，以及在此基础上结合复Wishart分布最大似然估计的Wishart非监督分类。而在各种基于散射机理的分类方法中，最广泛应用的是Cloude S R 等人提出的H/α方法[10,11]及Lee在此基础上提出的H/α-Wishart方法[12]。H/α方法利用极化相干矩阵的特征向量与特征值，计算获取目标散射熵H和代表地物散射机理的极化散射角α，并用这两个参数组成特征平面，对PolSAR数据散射机制进行分类。H/α-Wishart方法则以H/α方法对影像进行初始划分，利用Wishart距离进行迭代得到分类结果。由于H/α-Wishart方法采用的是C均值算法模式，故其分类结果中类别数目固定且分类效果受初分类影响较大，而H/α方法作为基于散射机理的非监督分类方法的一种，一方面由于散射机理与地物并不完全符合一一对应关系，故不可避免地存在地物类别分类混淆的问题，另一方面对于数据在H/α空间中的分布也存在较大的依赖，使用时适应性有限。

本文为弥补H/α-Wishart方法的上述不足，提出一种利用Pauli分解改进初分类的极化SAR影像非监督分类算法，首先利用总功率Span进行初始划分以保证最终分类类别数的可调控性，再利用Pauli分解的3个波段组成特征空间，通过迭代聚类的方式得到进一步的初分类结果，然后使用Wishart距离得到最终分类结果。实验部分使用2组极化SAR影像证明了算法的有效性以及对不同数据分布的适应性。

1 PolSAR图像H/α-Wishart分类方法

PolSAR数据的基本格式为2×2的Sinclair复散射矩阵，其矩阵形式为

(1)

式中h与v分别为水平极化与垂直极化，如Shv即表示以垂直极化发射、水平极化接收的回波强度。对于单基极化SAR系统，根据互易假设有Shv=Svh，此时Sinclair矩阵可以写成向量

(2)

式中Z为转置。基于此向量，可以得到极化相干矩阵T

(3)

式中*Z为共轭转置。通过对相干矩阵T进行目标分解，Cloude S R等分解出特征量熵H和散射角α[5]，再利用熵H和散射角α组成二维H/α特征空间，并根据经验数据设置了H/α平面划分的数值边界。Lee等人则在H/α划分的基础上结合极化SAR数据分布提出了H/α-Wishart算法[6]，利用最大似然判决准则可以得到衡量像素的相干矩阵〈T〉到第m类目标的相干矩阵之间的距离度量准则

(4)

即当像元的极化相关矩阵T满足d(〈T〉,Vm)≤d(〈T〉,Vj),j=1…,M,m≠j时，则将该像元归属为类别m。

2 基于Pauli分解改进的分类算法

H/α方法是一种简单而快速的非监督分类方法，能够粗略的对分类结果的散射机理进行解译指导。但由于只能得到像素的散射机理信息，而散射机理与真实地物难以满足一一对应关系，因此仍旧存在分类精度不高的问题。此外，Wishart聚类采用了C均值聚类的迭代模式，这种聚类算法的效果很大程度上依赖于初始类别的划分方式，不恰当的初分类方法往往导致迭代结果难以收敛于全局最优解。同时H/α方法受限于数据在H/α平面分布状况的特点也导致H/α-Wishart分类结果中的类别个数完全取决于数据在H/α平面中占有的类别个数。

针对上述情况，本文提出一种基于Pauli分解的初分类改进方法。首先，根据设置的目标聚类类别数，对极化总功率Span进行均匀划分，完成初分类；然后，利用Pauli分解得到符合视觉特征的3个波段，并在该特征空间中利用反复迭代的方式优化聚类中心；最后，再利用符合极化SAR数据分布的Wishart距离度量得到最终分类结果。算法详细流程如下：

1)使用3×3窗口的boxcar滤波削弱PolSAR影像中斑点噪声的影响；

2)计算极化相干矩阵及总功率Span;

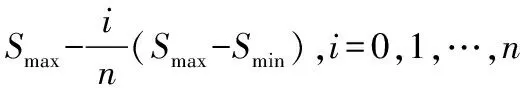
4)将Pauli分解的3个分量组成特征向量

令第j类的聚类中心为属于j类像素的相干矩阵均值

Cj=E(X),X∈j

获取新的聚类中心后，若存在k使得

d(X,Ck)≤d(X,Cp),p=1,…,n

则将该像素划分为第j类；迭代更新分类与聚类中心直到满足终止条件；

5)获取优化的聚类中心后，根据前一步的类别划分，再基于Wishart距离在相干矩阵组成的特征空间进行迭代分类；满足终止条件后输出分类结果。步骤(4)和步骤(5)两步的终止条件均为一轮迭代后改变类别的像素个数少于总像素的5 %或迭代次数达到阈值。

3 真实实验与对比分析

3.1 影像分类实验

选取2组数据进行分类实验。第一组数据采用美国航空航天局的L波段AIRSAR 机载全极化数据，该景数据采自美国旧金山海湾，影像分辨率为10 m×10 m。实验数据采用大小为663像素×807像素的区域子集，从伪彩色合成图和真实地物参照中都可以看到，该区域的地物类别主要有海洋、城市区域、植被和裸土。图1还展示了各方法分类结果。

对比图1(c)与图1(d)可以看到，基于Pauli分解改进初分类的分类结果中，马球场小部分像素被误分为植被的现象消失，海滩与海洋的区分精度有所提高，除部分分类细节有所改进外，两种方法的分类结果整体效果极为相近。

图1 旧金山影像及分类结果对比

作为对比，第2组实验采用AIRSAR在荷兰Flevoland地区获取的L波段全极化SAR影像，该景影像分辨率为12.10 m×6.6 m。实验数据采用大小为447像素×471像素区域子集。该实验地区主要地物类型均是一些形状规则的近似矩形的农作物，包括草地、土豆、甜菜、豌豆、油菜籽和裸土等地物。

对比图2(b)与图2(c)则可以看到，利用Pauli分解迭代进行初分类优化后，分类结果与基于H/α初分类的分类结果有显著差异。

图2 荷兰稻田影像及分类结果对比

从图3中可以看到，在荷兰稻田影像的H/α-Wishart方法分类结果显得更加杂乱，作物的混分比较严重，而基于Pauli分解改进初分类的分类结果作物田地内部的斑点相对较少，道路及其两旁的区域分类也更加准确。对比影像右上部分的分类结果同样可以看出，基于Pauli分解改进初分类的分类结果类别划分更加清晰，田地的边界明显，田地内部斑点明显减少。

图3 荷兰稻田影像分类结果细节对比

参照图4中的真实第五类别，选择了6类主要地物作为训练样本计算得到不同算法的分类精度及Kappa系数。

图4 Flevoland地区真实地物参考

从表1中可以看出，在H/α-Wishart算法的分类结果中，草地的分类精度是最低的，其原因是草地与裸土均为低熵表面散射，在H/α分类中不易区分，最终导致迭代分类后混为了相同的类别，而在基于Pauli分解改进初分类的分类结果中两者被较清晰地区分了出来。对于其他几个地物类别，油菜、豌豆等类别的分类精度提升明显，土豆、甜菜精度稍差但相距不大，裸土的分类精度则都非常高。从总体分类精度和Kappa系数来看，基于Pauli分解改进初分类的分类较以H/α作为初分类的Wishart迭代方法均有不小的提高。