立意于图形变换的“全等三角形”课例及分析
2019-06-22贺舞燕鲁建桥
贺舞燕 鲁建桥
[摘 要] 用运动、变化的观点认识全等图形,有助于学生感悟图形变换的价值和发展图形变换的意识.对于“全等三角形”这一课,文章立意于图形变换,在反复研课与反思的基礎上,不断地对该课教学进行重构与实践.
[关键词] 图形变换;全等三角形;教学方法;案例分析
图形变换是几何学的重要内容,它描述的是图形的变换方式和变换前后两个图形的关系. 图形变换具有使孤立的、离散的条件相互沟通的作用,它是解决几何问题的重要思想方法.两个全等图形可以看成是由一个图形通过变换得到另一个图形,用变化、运动的观点认识全等图形,有助于学生感悟图形变换的价值和发展图形变换的意识.
环节1:体验全等图形,明确方向
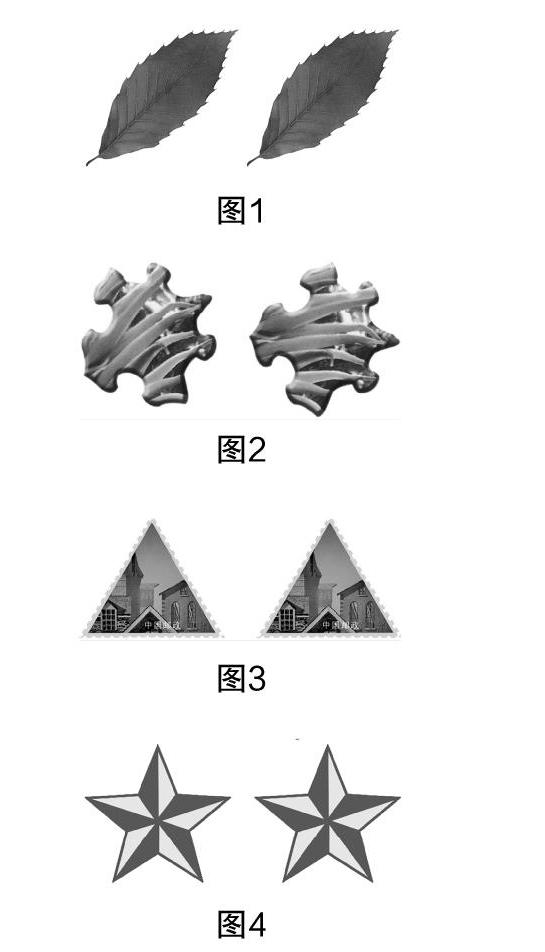
师:同学们注意过吗,生活中有许多形状和大小都相同的图形.例如,图1、图2、图3、图4中的各对图形.这样的各对图形有何特点?本节课一起来探究这个问题. (揭示课题并板书)
环节2:定义全等三角形,形成概念
师:现在请同学们把图1中的两个图形剪下来,并把它们叠在一起.问:同学们能发现什么?(图形课前发给学生)
师:好的. 图2中左边的图形做怎样的运动能使它与右边的图形完全重合?
生1:左边的图形先按顺时针方向转一下,再向右平移.
师:不错.那么图3和图4呢?
生2:这两个图形能重合.
师:要使这两个图形能重合,其重合的方法是什么?
生3:相对应的点要放一起.
师:同学们还能举出类似这样的生活中的例子吗?
生4:半径相同的两个圆.
生5:我手中的30度、60度、90度的三角板和张亮手中的相同角度的三角板.
生6:电脑中复制粘贴前后的两幅图片……
师:同学们说得非常好.一般地,能完全重合的两个图形叫作全等图形.特别地,能够完全重合的两个三角形叫作全等三角形.
师:两个全等三角形重合时,能互相重合的顶点叫作全等三角形的对应顶点,互相重合的边叫作全等三角形的对应边,互相重合的角叫作全等三角形的对应角.
师:为便于书写,用符号“≌”来表示全等.“∽”可理解为形状相同;“=”可理解为大小一样.例如,△ABC和△A′B′C′全等,可记作“△ABC≌△A′B′C′”,读作“三角形ABC全等于三角形A′B′C′”.一般地,用符号“≌”来表示两个三角形全等时,通常把对应顶点的字母写在对应位置上.
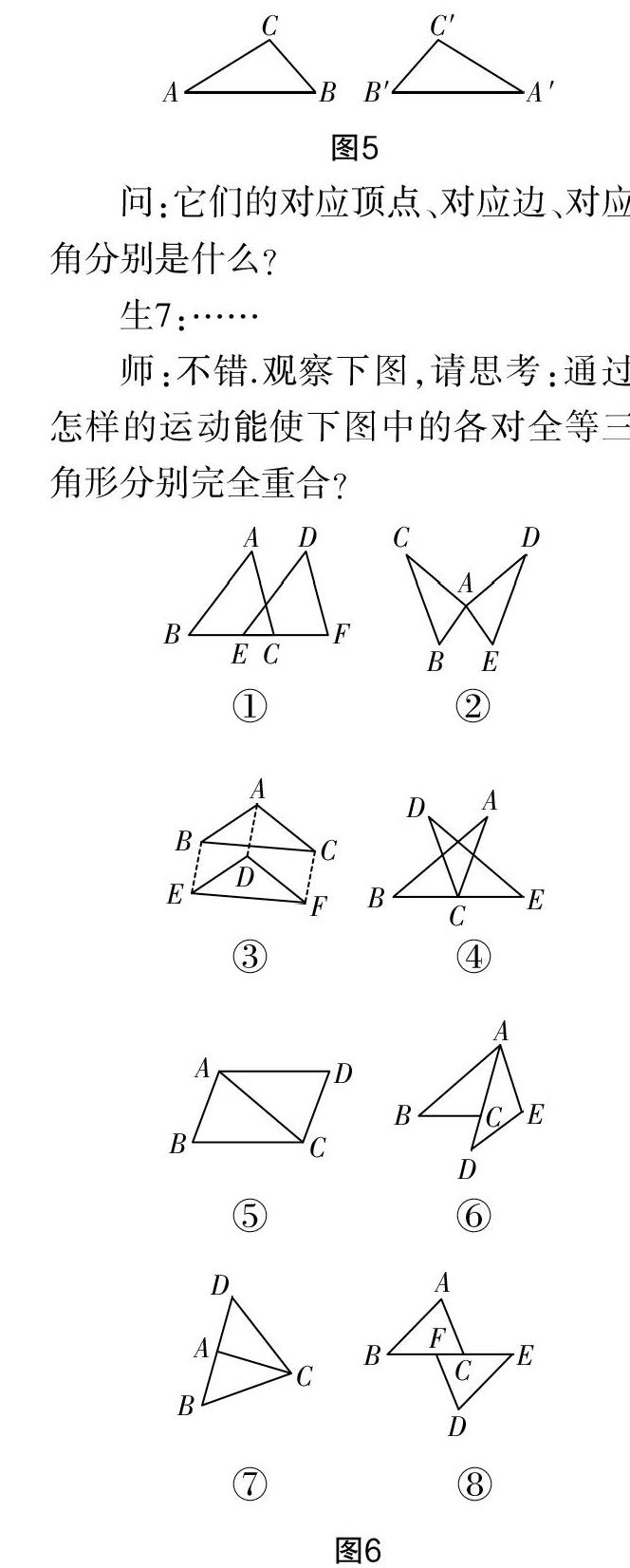
师:图5中的△ABC和△A′B′C′是全等三角形.
问:它们的对应顶点、对应边、对应角分别是什么?
生7:……
师:不错.观察下图,请思考:通过怎样的运动能使下图中的各对全等三角形分别完全重合?
生8:①△DEF沿CB方向平移;②△DAE沿过点A的直线翻折.
生9:③△ABC沿AD方向平移;④△DCE沿过点C的直线翻折.
生10:⑤△ACD绕AC的中点旋转;⑥△ADE绕点A旋转.
生11:⑦△DAC沿直线AC翻折;⑧△FDE绕线段FC的中点旋转.
师:好的. 找对应顶点、对应角和对应边时,经常要先想象三角形的重叠方式.
环节3:探索边角关系,生成性质
师:全等三角形的定义可以分解出两个命题:(1)若两个三角形能完全重合,则这两个三角形全等.(2)若两个三角形全等,则这两个三角形能完全重合.问:全等三角形的对应边、对应角分别相等吗?为什么?
生12:全等三角形的对应边、对应角分别相等.因为全等的两个三角形能完全重合.
师:好的.对应边、对应角分别相等的两个三角形是全等三角形吗?
生13:通过叠合实验可得:对应边、对应角分别相等的两个三角形是全等三角形.
师:好的.一般地,若两个三角形全等,则其对应边、对应角分别相等.若两个三角形的对应边、对应角分别相等,则这两个三角形全等.
环节4:尝试知识应用,提炼方法
师:现在请同学们思考下列两个例题.
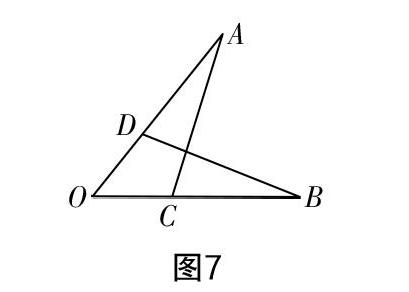
例1:如图7,△AOC与△BOD全等. 问:
(1)如何表示这两个全等三角形?
(2)若∠A与∠B是对应角,则其余的对应角和对应边分别是什么?
生14:△AOC≌△BOD.
生15:因为∠A与∠B是对应角,所以其余的对应角是:∠AOC与∠BOD,∠ACO与∠BDO;对应边是:OA与OB,OC与OD,AC与BD.
师:找对应点、对应角、对应边,你是怎样思考的?
生16:先想象重合前后的两个图形,再确定对应点、对应边、对应角.
教师补充:相等的边是对应边,相等角的对边是对应边,相等角的夹边也是对应边;类似的,同样可以得到找对应角的方法. 这些方法是找全等三角形对应元素的常用方法,以后我们会经常用到.
例2:如图8,AD平分∠BAC,AB=AC.问:
(1)△ABD与△ACD全等吗?为什么?
(2)BD与CD相等吗?∠B与∠C相等吗?为什么?
生17:△ABD≌△ACD.因为AD平分∠BAC,所以∠BAD=∠CAD,所以将图8沿AD对折时,射线AC与射线AB重合.因为AB=AC,所以点C与点B重合.因此,△ABD与△ACD能完全重合,即△ABD≌△ACD(全等三角形的定义).
生18:BD=CD,∠B=∠C.因为△ABD≌△ACD,所以BD=CD(全等三角形的对应边相等),∠B=∠C(全等三角形的对应角相等).
师:好的.同学们判断两个三角形全等有哪些经验?
生19:若两个三角形能完全重合,则这两个三角形是全等三角形.若两个三角形的对应边、对应角分别相等,则这两个三角形是全等三角形.
师:好的.已知两个图形全等找对应边或对应角,和已知对应边或对应角判定两个三角形全等是以后会经常遇到的两种基本题型.
师:一个图形通过适当的运动变为另一个图形,运动前后的两个图形有何关系?
生20:运动前后的两个图形全等.
生21:运动前后两个图形的对应边、对应角分别相等.
师:由此大家有何感触?
生22:图形运动能改变图形的位置,但不会改变图形的形状和大小.
生23:图形运动能实现量与量之间的相互转化.
師:好的.由于图形运动能使孤立的、分散的条件相互沟通,所以在解决几何问题时会经常使用图形运动的思想方法.
师:接下来,请同学们完成课后作业题,并在完成后,小组里进行校对与反馈.
环节5:回顾知识脉络,感悟收获
师:请同学们围绕下列问题反思与总结本节课的收获.
(1)本节课研究的内容和研究的方法是什么?
(2)判定两个三角形全等有哪些方法?全等三角形有哪些性质?
(3)寻找全等三角形的对应元素有哪些方法?
(4)你认为研究全等三角形有何意义?
全等三角形是认识三角形的继续——从一个三角形到两个三角形之间的关系,它也是一种特殊的相似变换. “全等三角形”的教学内容不仅包括全等图形和全等三角形的概念,用字母和符号表示全等三角形,及其他的性质与判定,也包括全等三角形性质与判定的形成与应用的过程和蕴含的图形变换思想等. 全等三角形的判定及性质为证明线段相等、角相等提供了重要的方法,研究全等三角形的方法具有普遍适用性.想象重叠方式、寻找对应元素等过程能培养学生的想象力、感知力和创新精神,其蕴含的图形变换思想是数学中的重要思想.
本课例根据教学内容的地位与作用及蕴含的教育价值,将本课教学立意于图形变换,以学生身边的题材为背景,从学生的认知发展水平和已有的经验出发,通过教师适度引导与学生自主探究相结合的方式,逐步使学生经历完整的认知过程.在“定义全等三角形”的教学中,既有“实验、演示、想象、判断、归纳、定义”的过程,以形成全等图形的概念并且感受使两个全等图形完全重合所要遵循的叠的规则,又有“演绎、表示、解释”的过程,以获得全等三角形及对应顶点、对应边、对应角的概念和用符号表示全等三角形的方法,也有获得概念之后的反思,以知道常见的使两个全等三角形重叠的运动方式和感悟其蕴含的图形变换思想.在“全等三角形的性质与判定”的教学中,既有分解定义的过程,以明确从定义中可以分解出性质与判定两个命题,又有根据定义判断与表达性质与判定的过程,以形成全等三角形的性质与判定.在“尝试应用”的教学中,既有用所获知识解决问题的过程,以巩固概念,又有解决问题之后的反思,以积累判断两个三角形全等及找对应边、对应角的经验,明确与全等三角形有关的两类题型,感悟图形变换的价值.在“回顾与感悟”的教学中,既有教师问题引导下学生的自主思考与交流,又有教师的总结.这体现了过程教育和学为中心的教学模式,能实现“参与定义全等三角形的活动,能说出全等三角形及对应顶点、对应边、对应角的概念,能知道并会用字母和符号表示全等三角形的方法,能感悟获得全等三角形概念的过程和蕴含的抽象思维、符号表示思想、图形变换思想;探索全等三角形的性质与判定,能知道从全等三角形定义中可以分解出性质和判定两个命题,理解全等三角形的性质与判定;参与尝试知识应用的活动,会用全等三角形的定义判定两个三角形全等”的教学目标.
因此,“全等三角形”的教学,不仅要关注涉及的数学结果,也要关注获得数学结果的过程和蕴含的图形变换思想等.这对发展学生图形变换的意识和懂得图形变换的价值有积极的影响.
