参与试题命制，提升专业素养

☉浙江金华第一中学 黄锦龙

2018年11月27日—29日金华市教育局教研室举行了深化普通高中课程改革高三数学教师培训活动，此次培训的最大亮点是以高三数学教学的命题视角为主题，举办了金华市首届高中数学现场命题比赛.笔者与另外两位同事一起组成学校代表队参加了命题比赛.规则是根据举办方提供的命题背景和命题方向，在三个小时内完成命题，自备电脑，可带资料，但不允许上网.以命题比赛为纽带组织教研活动，最大限度地调动了参会教师的培训热情，使每位教师都能从中受益.笔者作为参赛选手，命制的试题获得了一等奖，通过参加这次活动，与专家同行沟通交流，有力地提升了自己的专业素养.

一、命题现场

经现场抽签，试题是数列1号题，题目如下：

请根据所给定理及拓展推演编制一道高考数列大题，并对你的命题作出简要解答.

回顾浙江省2015年—2018年高考数学试题，数列部分都是一小一大两道试题，小题以考查等差数列与等比数列的概念及其基本量的运算为主，大题除2018年位置前移，前三年都是压轴题，主要考查数列的概念、递推关系与单调性等基础知识，还有不等式及其应用，同时还考查推理论证能力、分析问题和解决问题的能力，属于难题.因此，对现场命制试题的理解为根据数列的递推关系，通过合理变形与有效放缩，运用裂项相消法求和，从而实现不等式的证明，属于压轴题的难度.

命题的着眼点就是p的选取.是选择常数还是表达式？关于这一点我们的想法很快就统一了，那就是取p为表达式，取进而可变形为这样便可以得到一道试题，但感觉离命题的要求还有一定的差距，怎么办？联想到一道作业题：数列{an}的通项公式为（n∈N*），求其前n项和.

试题点评：本题考查数列的通项公式、裂项相消法求和等基础知识与基本能力，以及灵活运用放缩法来证明不等式，深入考查学生分析问题和解决问题的能力，以及计算与推理论证能力.试题命制紧扣题眼“p”，通过对“p”的改造，编制了一道集数列与不等式于一体的有一定难度的综合试题.

二、再次命制

三个小时的命题比赛，紧张而又活泼，既是自由思想的创新火花，又是专业素养的集中展现.参加完试题命制比赛后，笔者还沉浸在试题命制的过程中，被试题命制所给的定理所吸引，回顾上述现场命制的试题，脑海中还是一直在问：能否对“p”再进行改造？基于这样的念头，经过仔细琢磨与推敲，又有所收获.

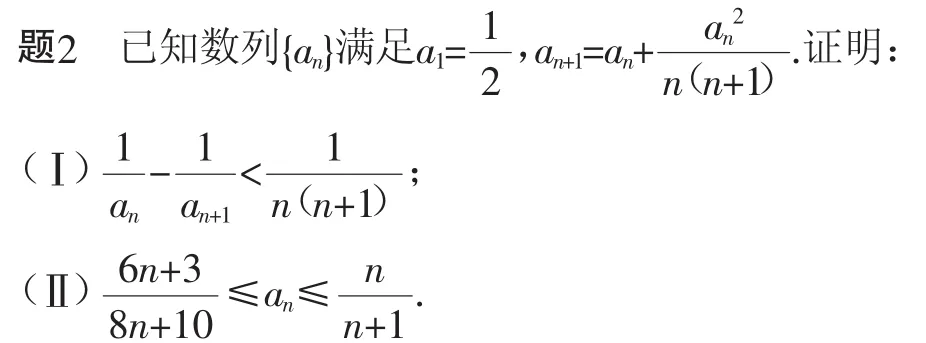
试题点评：上述两道试题的命制遵循能力立意，在命题构思上坚持用数学基本方法来解决数学问题，试题语言简洁，且问题清晰，解答富有层次感，故其都能深入考查学生运用不等式的基本性质进行推理论证的能力和熟练运用裂项相消法进行数列求和的运算求解的能力.

三、命题感想

1.命制试题是教师的必备基本功

“备、教、批、辅、考”是教师教学工作的五个环节.教学评价是数学教学活动的重要组成部分，教学评价的目的既是考查学生学习的成效，又是考查教师教学的成效.

新课程标准指出，要改变单纯依赖一张试卷的评价方式，丰富日常评价方式.无论是作业、测验等日常评价，还是学考、高考等考试评价，都离不开试题、试卷.在实际工作中，教师提供给学生巩固所学知识的练习或试卷基本上都是“拿来主义”，主要来源有两种：一种是直接购买练习题或试卷；一种是到网上下载练习题或试卷.好一点的做法是把几份试卷加以拼接与组装，而这样做或多或少会存在一些问题.比如，试题是否具有针对性？试卷能否针对学生学习的实际情况，在基础知识与基本方法的落实上实现全覆盖？要想有效地检测教学和学习效果，并提高课堂教学质量，最好的办法就是根据学情来命制试题.

命题、组卷是教师的一项经常性工作，同时也是教师进行创造性教学活动的基本功.对于我们教师而言，每天的课堂和作业都离不开命题，如果能做好命题这个工作，那么对我们的教学工作就会有很大的帮助.命制试题就要努力做到目的明确、内容科学、形式优美、解法合理.命制一道好的题目，需要考虑多方面的因素，课标怎么要求？重点、难点是什么？方法是什么？基本知识是什么？数学思想是什么？考查什么能力？题目面对什么样的学生？正所谓“根虚本不固，源浊流难清”，在命题方法上，我们要“博观约取，见微知著”.笔者的体会是，首先是要熟悉课本中的例题、习题，这些例题、习题反映了相关数学理论的本质属性，蕴含着数学重要的思维方法和思想精髓，尝试以课本中的例题、习题编制试题是命制试题的重要途径；其次是要多做题，可以从近几年的高考试题分类整理入手，抓住“点”并集中做某个专题，但也要完整地一份一份做高考题，从“面”上既能宏观把握学考框架，又能微观掌握知识技能、感悟思想方法和学科核心素养，为命制试题积累素材；第三是根据新课程标准，结合考纲，选择承载着基本原理和思想方法的题目并对其进行变式探究，如条件或结论的探究（增加、减少或变更条件）、结论的探究（结论是否唯一）、引申探究（命题是否可以推广）、类比探究等，将问题的拓展及引申的过程加以演绎就能命制出一道道精彩的试题.

2.在命制试题中提升专业素养

如何让教师从会解题到能命题转变是提升教师专业素养的关键.命制试题既可以大幅度地提高教师的解题能力，提升课堂教学水平，又可以延续教师的职业生命，丰富教师的人生阅历.

命制试题是一项严肃且复杂的工作.命制的试题不仅要突出对数学基础知识、基本技能和基本方法的考查，更要重视对数学思想方法的考查，注重对数学应用意识和创新意识的考查，而且要立意新颖、形式创新，能凸显人文价值，考查学生的个性品质，有适当的难度和可信的区分度.命制试题首要的是确保试题的科学性，科学性是对数学试题本身的结构和叙述的合理性、严谨性和清晰性的基本要求.一个不符合科学性的试题，不仅浪费考生的宝贵时间，而且会对解题者产生误导，尤其对考生的逻辑思维能力的形成和发展带来损害.因此，要对命题者提出很高的要求，需要命题者有丰富的教学经验、深厚的教学功底，工作耐心细致，勤于钻研教材与试题，具备严谨的科学素养和团结互助的合作精神.

一个好的数学教师应该是“能上课、能做题、能命题”.通过命制试题，能够提升教师理解教材、运用教材的能力，使教师不仅知道要教什么，而且更懂得怎样教，如何才能教得好.参与试题命制，一方面，培养教师的实践反思意识，围绕命题要求，联系自己的教育教学实践进行反思，摆出问题，总结过去，厘清思路，形成体会，提出困惑，寻求对策；另一方面，培养教师的问题研究意识，促使自己深入钻研教育教学业务，加深并拓宽专业知识，全方位获取信息，多角度拓展视野，不断提升自身专业素养.

3.通过命制试题落实核心素养

作为数学教育的实践者，特别是一线教师，如何发展学生的“核心素养”？课堂教学该怎么做？核心素养如何落实在课堂？这都是数学教师要思考的现实问题.核心素养的落实需要通过学科知识的学习，并脚踏实地付诸行动.笔者认为，依据学情、教学目标与考纲要求，通过改编命制习题、试题，将核心素养承载其中，学生通过练习就能不断使核心素养在潜移默化中落实.如在复习异面直线及其所成的角时，改编命制了这样一道习题：已知异面直线a，b所成的角为50°，过空间一定点P最多可作n条直线与直线a，b所成的角均为θ，则下列判断不正确的是（ ）.

A.当θ=65°时，n=3

B.当n=1时，θ只能为25°

C.当θ=30°时，n=2

D.当θ=75°时，n=4

这道题不仅将抽象的概念发展为具体的思维，而且在解题中发展学生的直观想象素养与逻辑推理素养.又如，在复习基本不等式时，编制了下面一组题目：

（1）已知a，b为正实数，且（a+b）（a+2b）+2a+3b=3，则3a+4b的最小值为______.

学生在解决这些问题时，需要理解并掌握基本不等式及运用基本不等式求最值的原理与方法，促使学生将陌生的问题转化为熟悉的问题，将复杂的问题转化为简单的问题，在解题中积累基本活动经验，发展数学抽象、逻辑推理、数学运算等核心素养.