带钢热连轧机工作辊动态温度场仿真与冷却工艺优化

孙业中 刘国勇 孙长福 李晓杰 宋 鸣

(1:上海宝钢股份有限公司 上海201900；2:北京科技大学机械工程学院 北京100083)

1 前言

在带钢热轧生产过程中，由于工作辊所受热载荷及冷却散热条件的空间分布不均匀，造成了工作辊沿各个方向温度分布的不均匀。其中，轧辊温度轴向分布的不均匀及其在轧制过程中的动态变化，将通过轧辊的热膨胀及其动态变化改变轧辊的在线辊形并影响承载辊缝形状，从而影响带钢的板形。因此，研究带钢热轧过程工作辊的热行为，对于提高产品板形质量以及厚度与表面质量、改善轧辊的表面磨损行为都具有重要意义。

近些年来，国内外学者开展了大量的相关研究工作。国际上，Ginzburg等用二维有限差分模型研究了边界条件、热交换系数以及各种设计参数(冷却水流速、压力等)对工作辊温度的影响[1]。Saboonchi等建立了二维有限差分模型，研究了冷却水喷射的几何参数，包括喷嘴角度、喷嘴到工作辊距离、喷嘴类型等对工作辊温度场的影响[2]。Abbaspour 等研究了带钢宽度、带钢温度、间隙时间、压下量等对工作辊温度场的影响[3]。在国内，Xuan-li Zhang等利用有限差分法建立了轧辊的二维轴对称模型，研究了带钢宽度和窜辊对工作辊热辊形的影响[4]。Lian-sheng WANG等采用一种二维交替差分的新方法建立了工作辊的二维热凸度模型，并且研究了轧制节奏和带钢宽度对于工作辊热凸度的影响[5]。Chang-Sheng Li等通过有限元方法建立了工作辊的三维温度场模型，研究了工作辊表面温度在轧制过程的变化规律，其计算结果得出工作辊在轧制过程的最高温度为593℃[6]。Ning-tao Zhao等研究了在轧制无取向硅钢过程中，轧制速度和窜辊对工作辊温度场和热辊形的影响[7]。东北大学的史静对于工作辊横移策略、热轧过程摩擦热和变形热、周围介质间热交换系数、带钢温度分布对工作辊温度的影响做出了研究[8]。北京科技大学张鹏雁对于轧件宽度、轧件温度、轧制节奏、环境温度等对工作辊温度的影响进行了研究[9]。孔祥伟采基于ANSYS有限元软件，对工作辊的温度场进行了仿真，动态分析了热轧时工作辊的升温过程[10],郝龙等人利用有限差分法建立工作辊温度场及热变形的数学模型,并利用 VC++平台进行模拟研究,建立适合在线计算的快速模拟软件[11],孔繁博对首钢某热轧1580生产线工作辊冷却方式进行改造, 从而获得较好的工作辊热凸度轮廓曲线，轧制出板形和表面质量良好的带钢产品[12],娄蕾完善了包含热凸度模型和磨损模型的板形程序，利用热凸度和磨损与板凸度的关系，结合首秦现场实测数据，对热凸度模型和磨损模型进行了验证，模型计算值与实测值吻合良好，充分说明了模型的准确性[13]。

综合文献发现，以往的研究没有对轧制工艺参数、冷却系统参数等对工作辊辊温变化规律及轴向辊温分布的影响进行系统的研究。本文基于ANSYS有限元软件，建立工作辊二维非稳态温度场的计算模型，探讨上辊、下辊辊温的差异，入口与出口水量分配比例、轧制速度、初始辊温分布等对辊温的影响。通过设计正交试验，采用直观分析和方差分析方法，研究入口与出口水量分配比例、轧制速度、工作辊中部与边部的水流密度比值对工作辊轴向辊温分布的影响程度，并在此基础上得到最优的工艺条件。

2 有限元模拟

2.1边界条件

根据实际生产条件，上工作辊圆周方向的热交换过程可等效为 10 个区域，如图1 所示。每个区域的热交换形式如表1所示。

图1 上工作辊边界条件

区域换热形式AB工作辊与带钢的接触传热BC、JA工作辊与空气的对流传热以及带钢的辐射传热DC、JI挡水板间的积水换热DE、HI冷却水与工作辊的强制对流换热EF、GH工作辊与空气的对流换热GF工作辊与支撑辊间的接触传热

下工作辊圆周方向的热交换过程可等效为8 个区域，每个区域的热交换形式,如图2 表2所示。

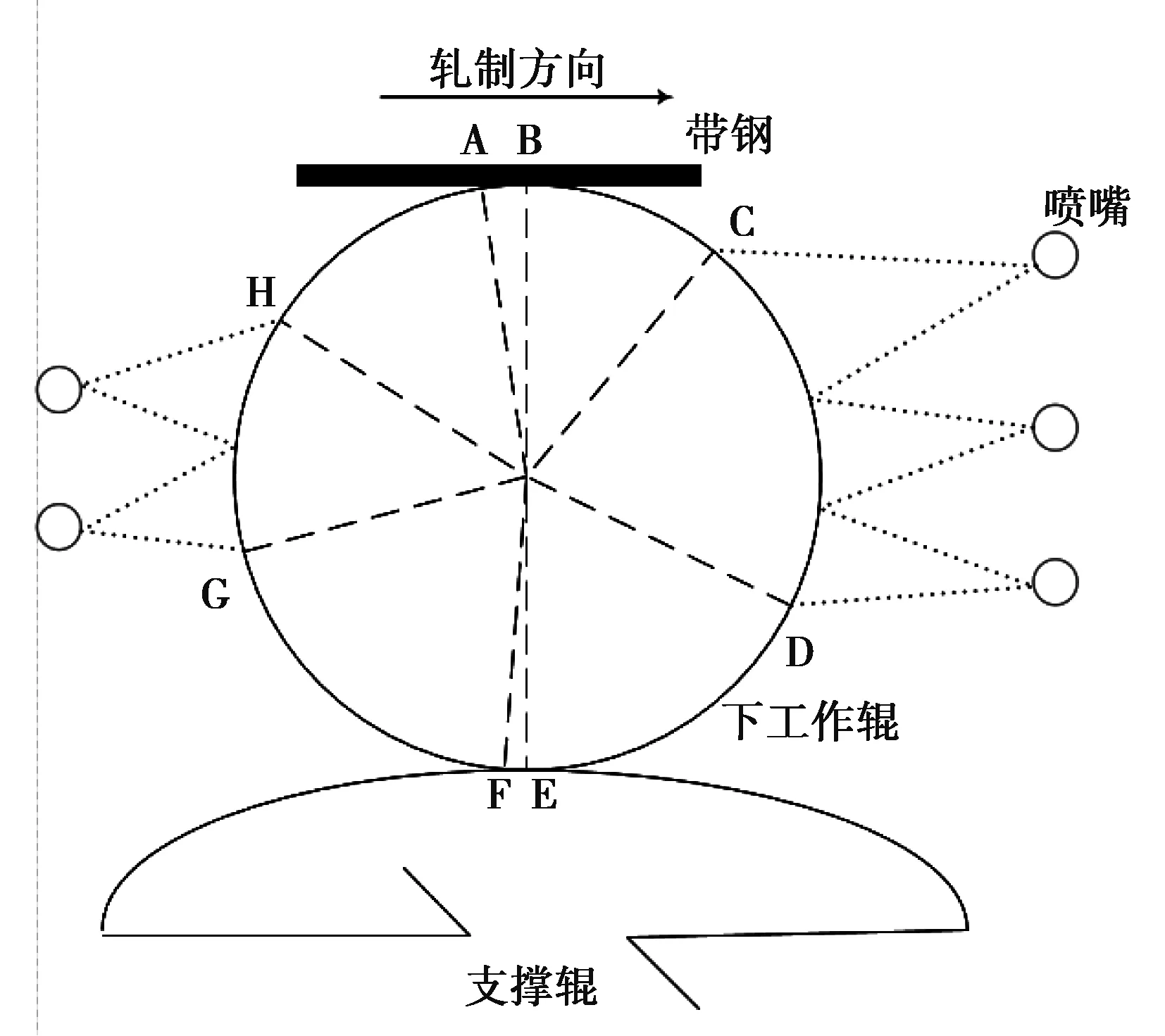
图2 下工作辊边界条件

区域换热形式AB工作辊与带钢的接触传热BC、HA工作辊与空气的对流传热以及带钢的辐射传热CD、GH冷却水对工作辊的强制对流换热DE、FG工作辊与空气的对流换热以及流水对工作辊的冷却EF工作辊与支撑辊间的接触传热

本文边界条件的换热系数主要参考相关文献[14-20]进行计算。

2.2有限元模型的建立

轧辊温度场是一个三维非稳态系统。在轧制过程中，轧辊轴向、径向和周向的温度都要发生变化。求解工作辊的温度场应该从分析工作辊的三维温度场变化出发，但这会成倍增加求解的复杂性和求解的计算量。为提高求解速度，满足计算精度，本文基于ANSYS有限元软件，建立了两种温度场模型，在分析轧辊内部不同深度处温度变化时，采用径向有限元模型，不考虑轴向传热；另外建立了轧辊轴对称温度场模型，忽略周向传热，主要是进行轧辊轴向温度分布规律的研究。

2.2.1 工作辊横截面内温度场模型 为了研究圆周方向冷却水系统布置对轧辊温度场的影响，有必要建立工作辊横截面内温度场计算模型。忽略工作辊轴向的热传导，只考虑径向和周向的热传导，利用ANSYS软件，取垂直于轧辊轴向某一截面进行分析研究，选取Plane55单元，建立工作辊径向温度场有限元模型，如图3所示。由于轧辊热量的交换主要发生在其表面，即表面热梯度较大，因此对轧辊表面层网格进行径向加密。

为了能够真实的反应轧制过程中工作辊的旋转过程，在进行加载时，将工作辊模型固定不动，给定一个与工作辊旋转方向相反的速度进行加载。施加了这种反向的边界条件，就可得到工作辊真实的瞬态温度场。

图3 工作辊径向有限元模型

2.2.2 工作辊轴对称温度场模型

建立工作辊轴对称温度场模型对于研究工作辊轴向的温度场分布是有帮助的。忽略工作辊圆周方向的热传导，通过ANSYS有限元软件，采用Plane55单元，建立工作辊轴对称平面温度场模型，如图4所示。由于工作辊表面和与带钢接触区域温度梯度较大，将这部分网格加密。

在对轴对称模型进行加载时，根据工作辊圆周方向的边界条件，针对每个区域的角度以及工作辊转速，计算出工作辊在该区域的加载时间，然后根据加载时间和边界条件对模型进行动态加载。

图4 工作辊轴向温度场有限元模型

3 工作辊温度场的关键影响因素及其影响规律仿真研究

针对某钢厂2250生产线，对精轧机工作辊温度场进行研究，平均轧制节奏为73s / 60s(轧制时间 / 间歇时间)。

3.1上辊与下辊上机辊温差异的影响

以F2机架为研究对象，利用径向模型计算上辊、下辊的温度。图5为轧制过程中，轧辊旋转一周的时间内，上工作辊及下工作辊表面节点温度的变化情况。从图5中可以看出，在轧制过程中，上工作辊的表面温度比下工作辊的表面温度高，这是上辊及下辊不同的冷却条件导致的。由于下辊没有挡水板的遮挡作用，挡水板的积水换热变成冷却水的流水换热；另外上辊的冷却水在轧钢时会落到下辊上，也会加强下工作辊的冷却效果。

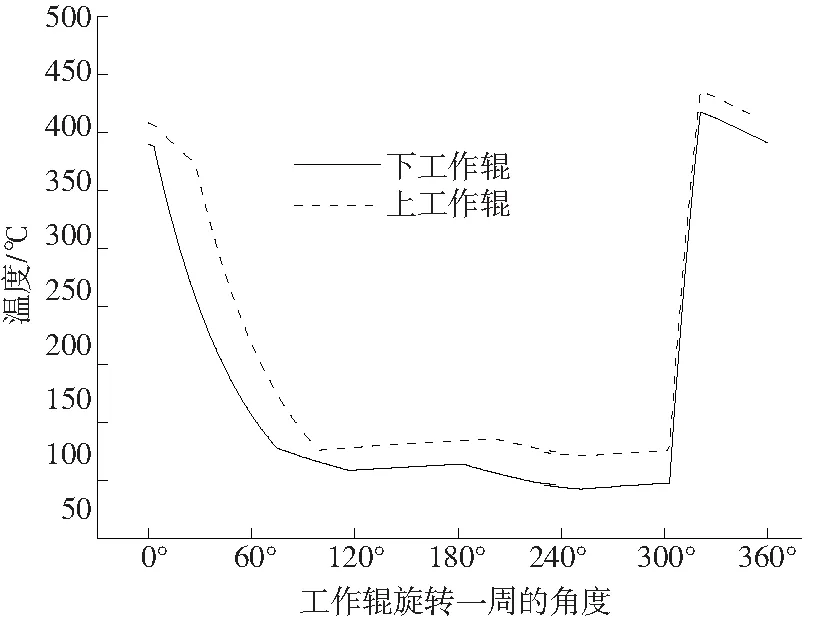
图5 上工作辊及下工作辊轧制期间表面温度比较

图6为上工作辊及下工作辊的下机实测温度比较，考虑到对称性，只测量辊身长度的1/2，每隔100mm测一点，下文皆同。从图6中可以看出，与下工作辊相比，上工作辊的下机实测温度整体要高，这也印证了下工作辊的冷却效果要好于上工作辊的冷却效果。

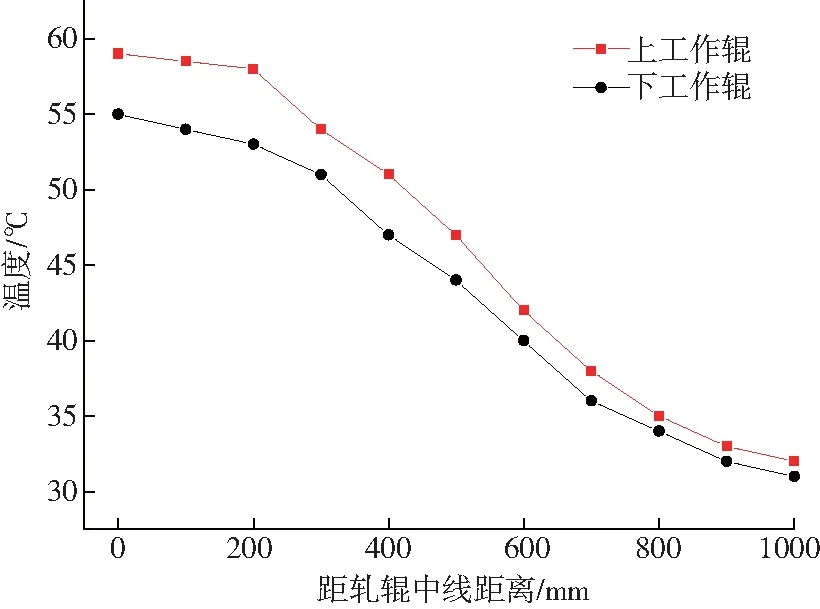
图6 上工作辊及下工作辊下机实测温度比较

在现有的技术方案下，上辊及下辊的冷却喷嘴布置方式普遍均一致，上辊及下辊的冷却水量一致。基于上述计算分析，可将下工作辊的冷却水量适当减小，可达到节约水量的效果。

3.2入口与出口水量分配比例的影响

工作辊圆周方向冷却水流量的分配比例对工作辊的冷却有着很大的影响。以F1机架为研究对象，结合建立的计算模型对六种分配比例(入口侧25%，出口侧75%；入口侧20%，出口侧80%；入口侧17%，出口侧83%；入口侧14%，出口侧86%；入口侧12%，出口侧88%；入口侧0%，出口侧100%)进行了计算。

图7为六种入出口水量分配比例的工况下，工作辊旋转一周的过程中表面温度的变化情况。六种工况下，工作辊上升的最高温度都是在 520℃左右，但是出口侧工作辊表面冷却到的最低温度有所不同。当出口侧分配比例为100%时，工作辊表面温度最低能降到86℃，其它5种分配比例下，工作辊下降到的最低温度分别为96℃、97℃、100℃、106℃、117℃。为了缩短辊面处于高温状态的时间，控制氧化膜厚度，必须尽快使辊面温度降下来，通过加大出口侧冷却水量、减少入口侧水量来加强工作辊的冷却效果。

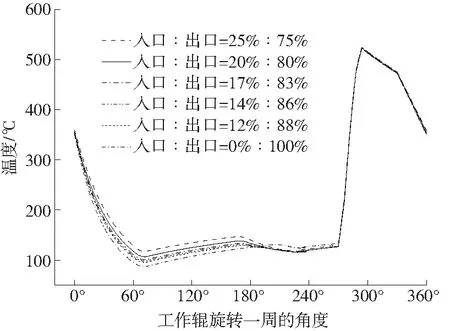
图7 工作辊温度与出入口水量分配比例的关系

图8和图9分别为12%：88%的入出口水量比例和0%：100%的入出口水量比例两种情况下，工作辊的下机温度云图。通过比较，两种情况下工作辊表面温度相差不大，都在63℃左右，可以看出，关闭入口水不会对工作辊的温度产生不良影响。因此，可以考虑关闭入口水，只开出口水的方式，迅速将工作辊表面的热量散失掉，缩短辊面处于高温状态的时间，有利于维护工作辊辊面氧化膜，减少带钢表面氧化铁皮缺陷。

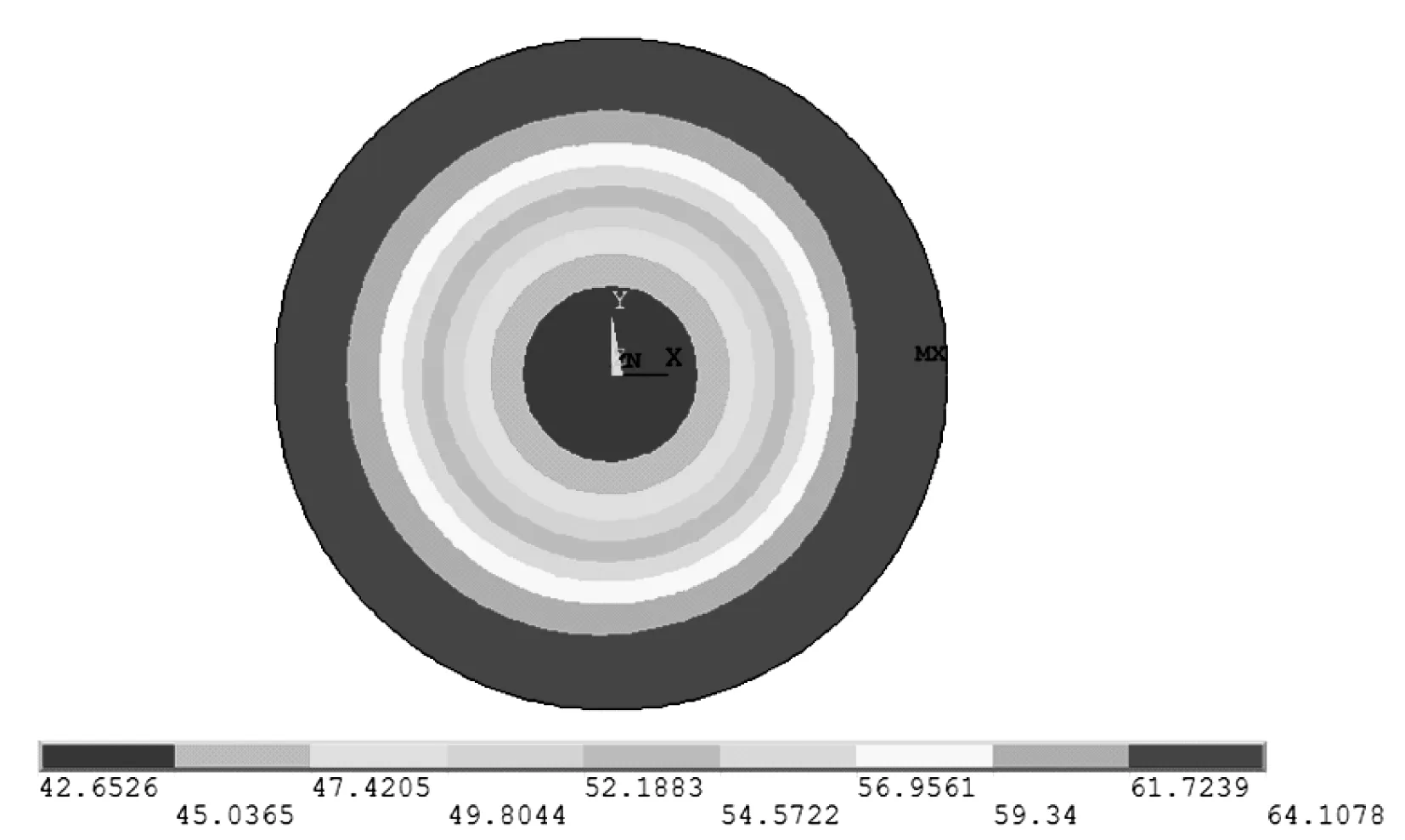
图8 12%：88%的入出口水量比例的下机辊温云图

图9 0%：100%的入出口水量比例的下机辊温云图

3.3轧制速度的影响

在其它轧制条件相同的情况下，模拟工作辊速度分别为1.2m/s、2.2m/s、3.2m/s时的工作辊温度。图10—图12为不同工作辊速度条件下，距工作辊辊面不同深度处节点温度的变化曲线。可以看出，轧制速度越慢，工作辊表面温度越高， 原因是轧制速度越慢，工作辊与轧件接触的时间越长，工作辊吸收的热量越多。同时，距表面越深的区域，温度变化受轧制速度的影响越小，在距表面2mm以内的区域，受轧制速度影响大；对距表面深度大于2 mm处的区域，影响较小。可以看出，轧制速度的影响具有“浅层效应 ”。

图10 轧制速度为1.2m/s时的工作辊温度

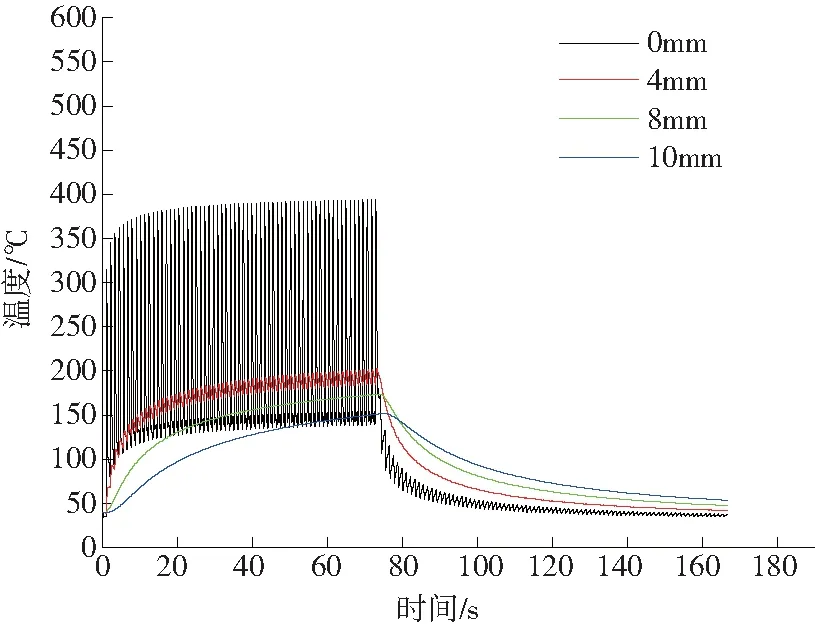
图11 轧制速度为2.2m/s时的工作辊温度

图12 轧制速度为3.2m/s时的工作辊温度

3.4初始辊温分布的影响

对工作辊中部与边部初始温差分别为0℃、20℃、40℃三种情况进行辊温的计算。图13—图15分别为轧制第3块、第5块、第10块带钢时三种初始辊温分布情况下的工作辊轴向温度。可以看出，随着轧制带钢块数的增加，初始辊温的不同对于工作辊轴向温度的影响越来越小。工作辊轴向温度分布在经过轧制5块带钢即可稳定。在轧制第10块带钢时，在轧制区域内，三种初始辊温情况下的工作辊轴向温度分布几乎一致，最大温差在1℃以内。

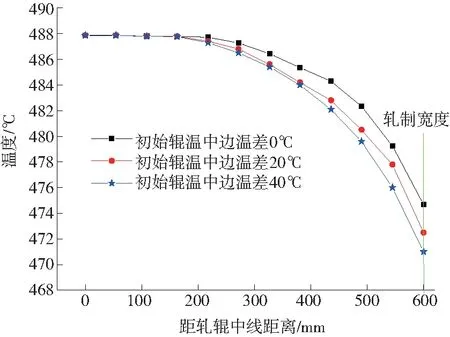
图13 轧制第3块带钢时不同初始辊温条件的轴向辊温

由此可知，随轧钢块数的增加，初始辊温分布对于工作辊轴向温度的影响越来越小，最终趋于一致。

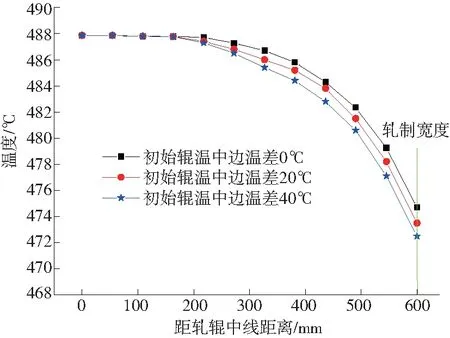
图14 轧制第5块带钢时不同初始辊温条件的轴向辊温

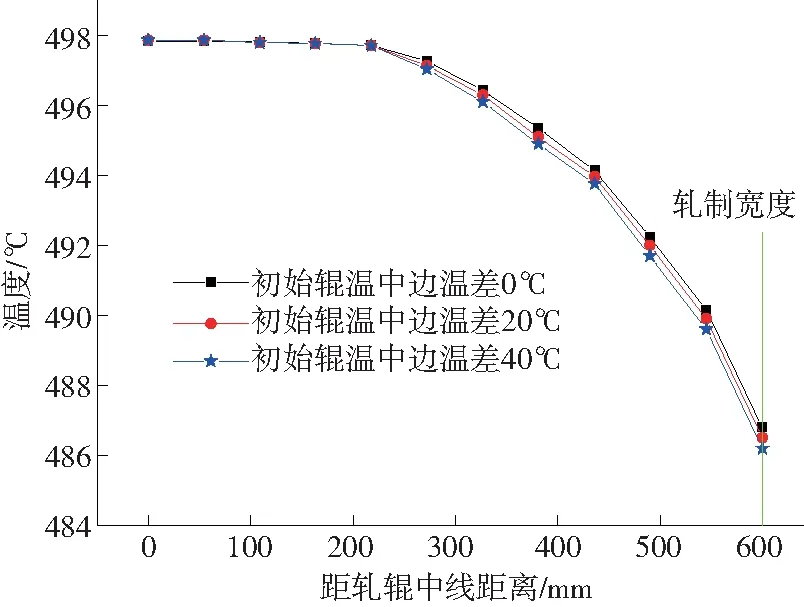
图15 轧制第10块带钢时不同初始辊温条件的轴向辊温

4 工作辊轴向温度分布的冷却调控工艺优化

4.1正交优化试验设计

在带钢轧制时，工作辊中部受热最大，散热最差，因此工作辊中部的热凸度一般最大。若轴向辊温分布不合理，会导致工作辊中部与两端的辊温温差及热膨胀差偏大，影响带材的板形质量。因此，对工作辊轴向辊温分布优化就显得尤为必要。

为了考察各影响因素对轴向辊温分布的影响效应，本文结合实践生产经验，选取入出口水量分配比例、轧制速度和工作辊中部与边部的水流密度比值作为试验的三个影响因素，采用正交试验的方法寻求轴向辊温分布最优的一组工艺参数。

以F1机架为例，每个影响因素设定3个水平，见表3。采用L9(34) 正交表安排一个3因素3水平的正交试验。

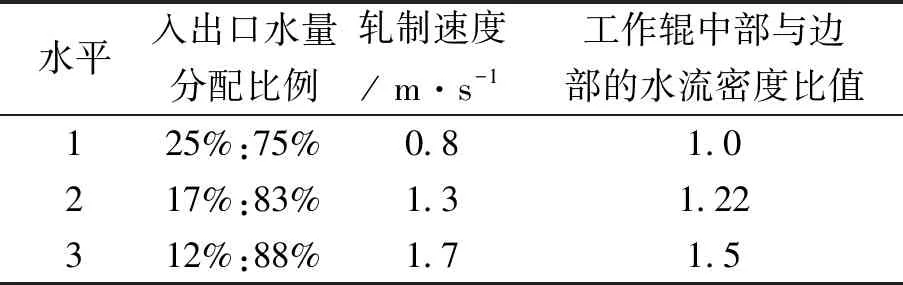
表3 正交试验因素与水平表

正交试验极差分析结果如表4所示，以第10块钢板(板宽为1200mm)的轧制期间内，在轧制区域内工作辊中部与边部的温差作为评价指标，表中A、B、C为三种影响因素，D为误差列。K1、K2、K3分别为各对应列 ( 因素) 上 1、2、3水平效应的工作辊中部与边部的温差之和，R为各对应列(因素)的极差。

表4 正交试验结果

4.2正交试验结果分析

(1)直观分析

如表3所示，对试验结果进行分析，因素A(入出口水量分配比例)、因素B(轧制速度)、因素C(工作辊中部与边部的水流密度比值)的极差分别为2、15.6、49.5，由此可以初步得到工作辊中部与边部的水流密度比值对轴向辊温分布影响最大，轧制速度次之，入出口水量分配比例影响效果最小。

(2)方差分析

正交试验的直观分析法简单直观，计算量小，但不能估计误差的大小，不能精确地估计各因素对试验结果影响的显著程度。因此需要对结果进行方差分析。正交试验的方差分析计算结果如表5所示。

表5 方差分析表

对于入出口水量分配比例，F< F0.1(2,2)，所以该因素对试验结果没有显著影响，不做标记；对于轧制速度，F0.01(2,2)>F> F0.025(2,2)=39，所以该因素对试验结果有一定显著的影响，记做 “ * ”；对于工作辊中部与边部的水流密度比值，F> F0.01(2,2)，所以该因素对试验结果有非常显著的影响，记做“* *”。

由方差分析可得到如下结论：工作辊中部与边部的水流密度比值对轴向辊温分布影响效果最为显著，轧制速度其次，入出口水量分配比例对轴向辊温分布没有明显影响。这与直观分析得到的结论是一致的。

(3)最优工艺条件的确定

由于试验指标是工作辊中部与边部温差，是越小越好，从表5可以看出，优方案应取各因素最小K值所对应的水平，即F1机架的入出口水量分配比例为12%：88%，轧制速度为1.7 m·s-1，工作辊中部与边部的水流密度比值为1.5。

以上以F1机架为例进行了正交优化试验分析，用同样的方法对F2—F7机架进行正交优化试验，得到F2—F7轧辊冷却的最优工艺条件如表6所示。

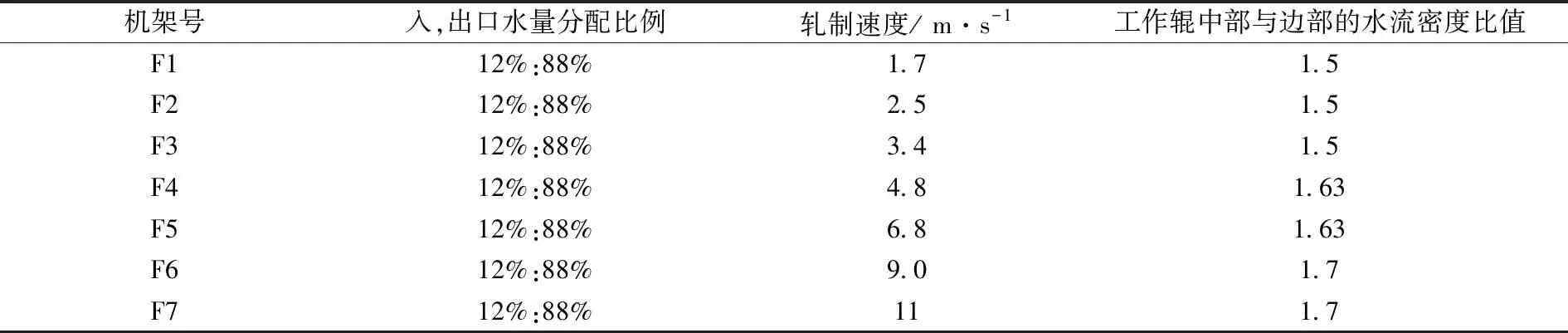
表6 F1—F7轧辊冷却最优工艺条件

5 优化冷却工艺的上机验证

为验证有限元模型对冷却工艺的计算精度，轴向辊温分布优化方案的合理性，采用表6所示的优化工艺方案进行上机轧制试验，图16为进行工艺优化试验后的下机辊温分布与工艺优化前的辊温分布比较。

从图16中可以看出，工作辊温度计算值与实测值基本吻合，本文的计算模型能够较好地模拟热轧工作辊的温度场分布。

工艺优化前，在轧制区域内，工作辊下机后中部与边部温差达到10～15℃；工艺优化后，在轧制区域内，工作辊下机后中部与边部温差会降到5～6℃。说明通过优化，很好地改善了工作辊轴向温度分布，减小了工作辊中部与边部的温差，对于改善工作辊热凸度有重要意义。

由此可以看出，本文的优化的轧辊冷却工艺方案是可靠的、合理的。

6 结论

本文基于ANSYS有限元软件，建立工作辊二维非稳态温度场的计算模型，对轧制工艺参数、冷却系统参数等对工作辊辊温变化规律及轴向辊温分布的影响进行了研究，得到以下结论：

(1)通过仿真计算和实测下机温度，上下工作辊冷却水量相同条件下，验证了上工作辊温度比下工作辊高。

(2)不同出口水量比对工作辊下机温度相差不大，关闭轧制入口冷却水不会对工作辊的温度产生不良影响。

(3)轧制速度越小，工作辊表面温度越高；距表面越深的区域，温度变化受轧制速度的影响越小，在距表面2mm以内的区域，受轧制速度影响大，轧制速度的影响具有“浅层效应”。

(4)随着轧钢块数的增加，初始辊温分布对于工作辊轴向温度的影响越来越小，工作辊轴向温度分布在经过轧制5块带钢即可稳定。在轧制第10块带钢时，在轧制区域内，不同初始辊温情况下的工作辊轴向温度分布几乎一致，最大温差在1℃以内。

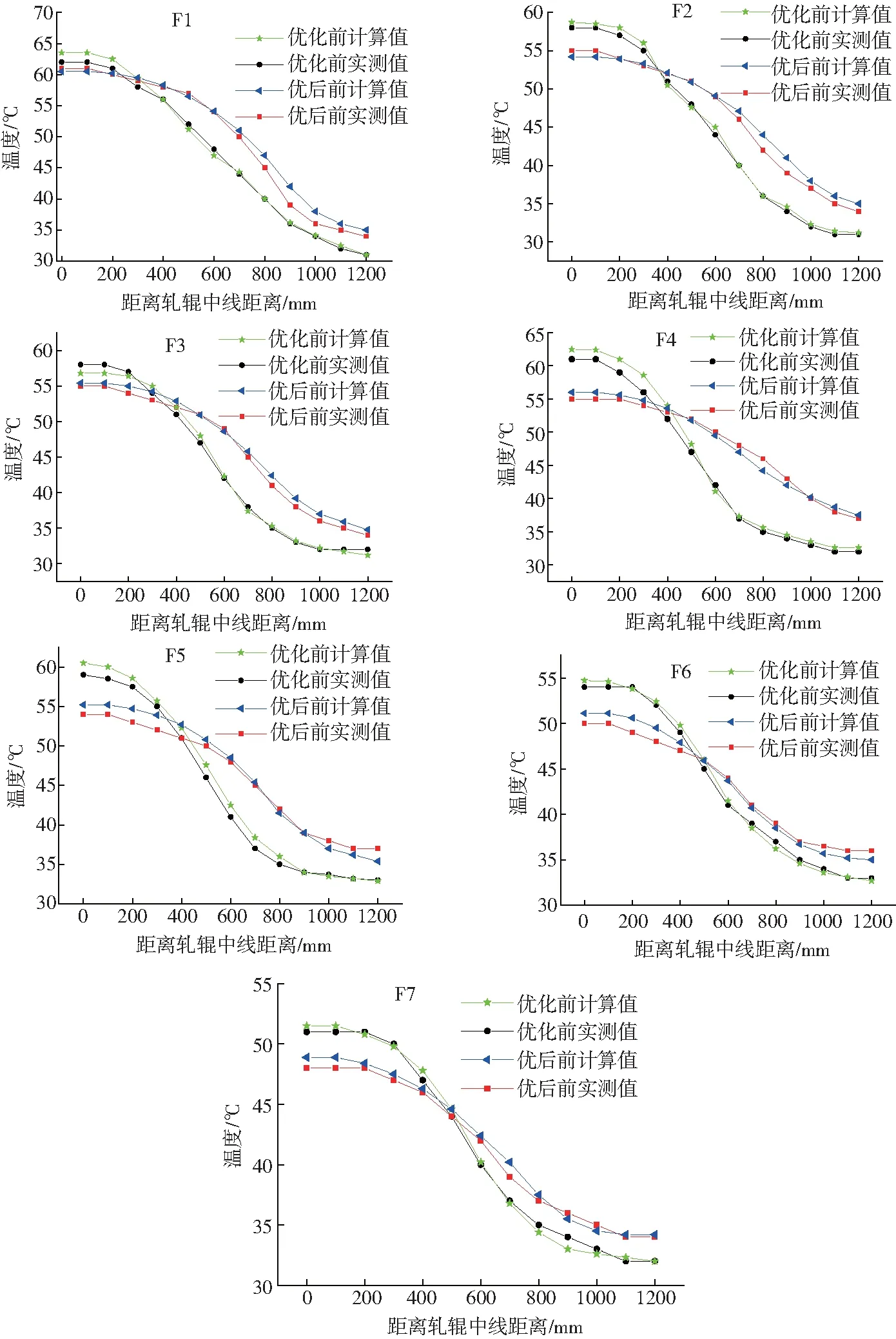
图16 工艺优化前与优化后的轴向辊温分布比较

(5)通过设计正交试验研究了不同因素对工作辊轴向温度分布的影响，工作辊中部与边部的冷却水量比例对轴向辊温分布影响效果最为显著，轧制速度其次，入出口水量分配比例对轴向辊温分布没有明显影响，得到了F1—F7轧辊冷却的最优工艺条件。

(6)为验证有限元模型的计算精度和轴向辊温分布优化方案的合理性，采用优化方案进行上机轧制试验，并进行优化试验后的下机辊温分布与优化前的辊温分布比较，可以看出工作辊温度计算值与实测值吻合较好，计算模型能够较好地模拟热轧工作辊的温度场分布。