磨粉机磨辊辊轴弯曲变形振动特性研究
2019-12-04张阳
张 阳
(太原科技大学机械工程学院,山西太原 030024)
0 引言
磨粉机的工作稳定性取决于系统的动力学特性,其中磨辊辊轴沿轴线方向的弯曲变形运动特性直接影响磨粉机的性能和生产质量[1]。辊轴在工作过程中发生弯曲变形运动的同时,也会受到辊间压力的影响。因此,综合考虑辊轴横向弯曲变形运动、刚性振动与辊间压力之间的耦合效应,是进行辊轴弯曲变形振动特性研究的基础,为建立辊轴弯曲动力学模型、预测磨辊运动规律、提高磨粉机生产质量提供了理论依据。
Kane T R等人[2]通过对作高速旋转运动的弹性梁进行动力学分析,发现弹性梁弯曲变形运动的动态响应随着转速的提高无限增大,首次提出“动力刚化”的概念;Boutagou Z E等人[3]从有限元的角度对弹性梁的动力学性质进行了研究;Banerjee A K等人[4]认为动力刚化现象的产生是由于刚性运动产生的惯性力作用在弹性体上而引起的;而Ider S K等人[5]认为动力刚化现象是由弹性体弯曲变形产生的应变量与刚性位移之间的非线性几何关系引起的。
以上研究表明弹性体的刚性振动与其自身的弯曲变形之间存在耦合关系。试验在上述研究基础上,将磨辊辊轴视为连续弹性体,对辊轴弯曲变形与刚性运动之间的耦合机理进行研究。通过运动学分析,建立磨辊辊轴弯曲变形动力学模型。
1 磨辊辊轴弯曲变形动力学模型
为了研究辊间压力对磨辊弯曲变形运动的影响,需要准确描述辊轴空间运动特征。
辊轴空间运动的等效分解见图1。
定义e0为惯性坐标系,在辊轴未变形时固结在中线的非惯性系定义为浮动坐标系e1。考虑辊轴两侧运动状态的不同,分别引入绕X轴、Z轴的转动角速度ω1、ω3,将辊轴空间运动等效为辊轴的平面运动与辊轴绕X轴和Z轴转动的叠加。同时考虑辊轴的转动,引入绕Y轴的转动角速度ω2。故可定义ω为系统的角速度列阵,且有

以半辊身长度的辊轴为研究对象,取辊轴轴身上的任意一点P进行研究。
辊轴运动学描述见图2。
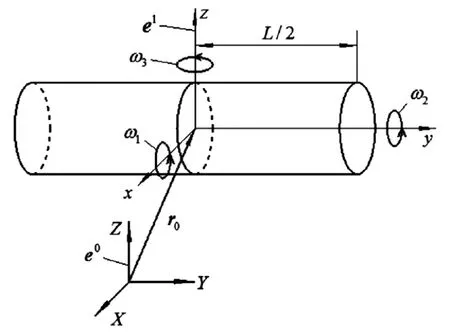
图1 辊轴空间运动的等效分解

图2 辊轴运动学描述
将P点对应的位移矢量记为u;辊轴发生弯曲变形前后,点P和P'在相对坐标系中的矢径分别为ρ0,ρ;点P在绝对坐标系中的矢径为r。则由平面运动的合成原理,矢径r可以表示为

由公式(2) 可得点P的加速度表达式

由公式(3) 可知,u可用来表征辊轴上任意一点的弹性变形运动,且有
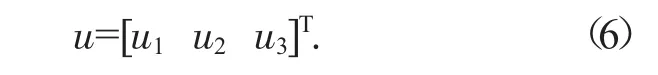

由欧拉-伯努利梁模型可知,辊轴的应变能可表示为

由图2可知,公式(9)中σy、εy分别为辊轴沿Y方向的正应力、正应变,考虑应力应变关系,并将公式(7)代入公式(9)得

式中:δW——辊间压力增量Δf所作的虚功。
将公式(8)、公式(10)代入公式(11)中,则磨辊辊轴刚柔耦合运动微分方程可表示为

其中,r01、r02、r03分别为辊轴刚性振动位移r0沿X、Y、Z轴的位移分量。考虑磨辊辊轴的受力状态,利用公式(12)来分析辊轴变形运动的动特性。基于弹性基础梁模型,磨辊间增量Δf应与辊轴弹性变形量w成正比,即

式中:K——辊间弹性系数。
将公式(13) 带入式(12),为了研究方便,模型忽略辊轴的刚性振动位移,且考虑辊轴绕Y轴的转动,则可得到磨辊辊轴的变形运动微分方程
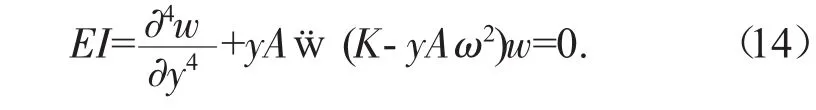
2 辊轴弯曲变形运动求解
为了求解辊轴的模态函数,需对式(14)进行求解。考虑半辊身长度为悬臂梁的情形,则辊轴两端的边界条件可写为
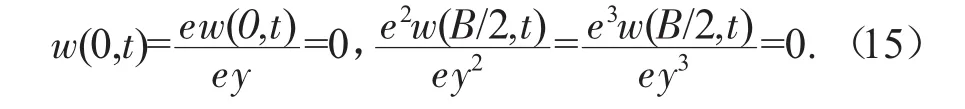
令:

其中,w(y)为辊轴弯曲变形振动的模态函数,将公式(16) 带入公式(15) 中,分离变量可得
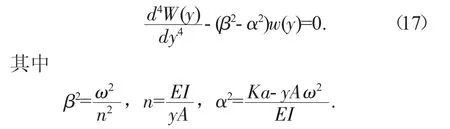
求解式(17),设方程的四个线性无关解为
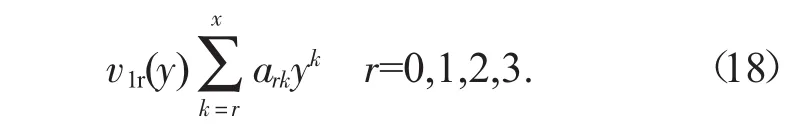
将公式(18)代入公式(17),可得ark的递推表达式为
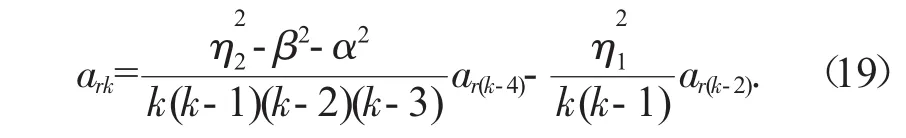
注意到,当k 则公式(17) 通解可设为 将边界条件(15)代入式(24),可得辊轴横向弯曲变形振动模态振型的解析解 将式(16)、(25)代入式(14)中,可得辊轴弯曲变形动力学方程 试验以某厂发生振动的磨粉机为研究对象,进行仿真分析。 计算参数见表1。辊轴一阶弯曲变形振动动特性曲线见图3,辊轴二阶弯曲变形振动动特性曲线见图4。 表1 计算参数 图3 辊轴一阶弯曲变形振动动特性曲线 图4 辊轴二阶弯曲变形振动动特性曲线 研究考虑了磨粉机工作过程中磨辊辊间压力对辊轴弯曲变形动力学特性的影响,通过运动学分析,实现柔性多体机械系统中可变形体的位移场描述,基于弹性梁变形理论和Hamilton变分原理,建立了磨辊辊轴弯曲变形动力学模型。模型的建立为准确预测磨辊弯曲动特性、提高磨粉机生产质量奠定了理论基础。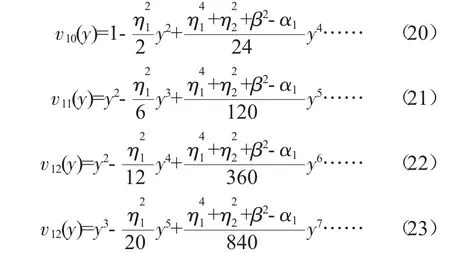
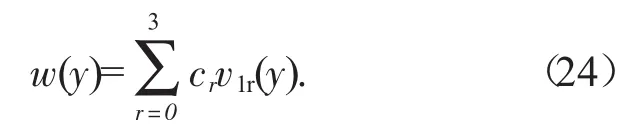

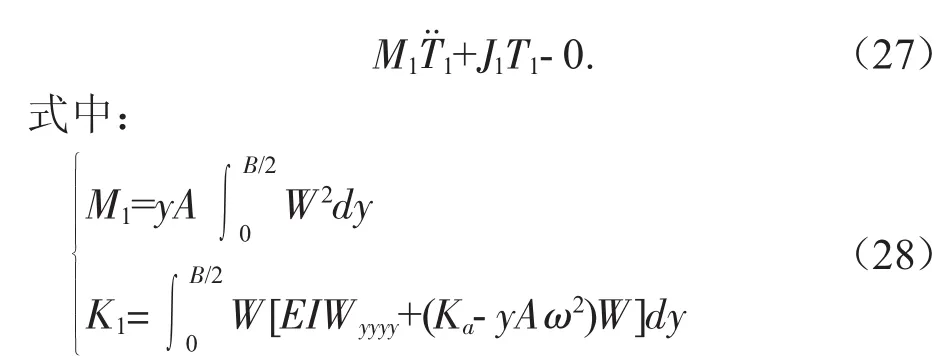



3 结论
