某些GV-分配半环的结构

蒲 楠 李 刚

( 山东师范大学数学与统计学院,250358,济南 )

1 引言及预备知识

设(S,·)为半群，对于任意的a∈S,若存在x∈S, 使得a=axa, 则称a为S的正则元. 若半群S的每一个元素都是正则元，则称S是正则半群[1].若对于正则半群S及任意的a∈S，存在x∈S, 使得a=axa,x=xax且ax=xa，则称S为完全正则半群.文献[2]深入地研究了完全正则半群.

半环(S,+,·)是一个带有二元运算“+”和“·”的代数，它满足以下条件：

(i)(S,+)是一个半群；

(ii)(S,·)是一个半群；

(iii)(a,b∈S)满足分配律，a(b+c)=ab+ac,(a+b)c=ac+bc.

定义1[3](X,≤)为分配格⟺代数系统(X,∨,∧)满足:

(i) 交换律(a∨b=b∨a,a∧b=b∧a);

(ii) 结合律((a∨b)∨c=a∨(b∨c),(a∧b)∧c=a∧(b∧c));

(iii) 幂等律(a∨a=a,a∧a=a);

(iv) 吸收律(a∨(a∧b)=a,a∧(a∨b)=a);

(v) 分配律((a∨b)∧c=(a∧c)∨(b∧c),a∧(b∨c)=(a∧b)∨(a∧c)).

定义2[3]半群S称为Archimedean半群，若对于任意的a,b∈S，存在一个自然数n(n∈Z+),使得an∈SbS.

定义3[3]半群S称为完全Archimedean半群，若它为Archimedean半群且包含一个本原幂等元.

定义4[4]半群S称为GV-逆半群，当S为GV-半群且S中任意正则元存在唯一的逆.

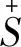
2 某些GV-分配半环的结构

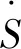
定义6设S为GV-半环，若对于任意的a,b,c∈S有a+bc=(a+b)(a+c),ab+c=(a+c)(b+c),则称S为GV-分配半环.

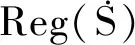
(a+b)(a+x)(a+b)=a+bxb=a+b,

(1)

定义7设S为GV-逆半环，若对于任意的a,b,c∈S有a+bc=(a+b)(a+c),ab+c=(a+c)(b+c),则称S为GV-分配逆半环.

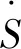
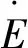
e=e(e+f),e+f=(e+f)(f+e)(e+f),

(2)

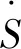
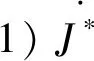
对于任意的c∈S，因为S为分配半环，所以

(3)

(4)

为分配格.

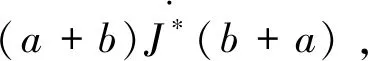
定义9设S为任意半环，对于任意的a,b∈S,有

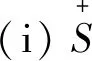
(ii) ∀a,b∈S,a(a+b)a=a;

(iii) ∀a,b∈S,(a+b)(b+a)(a+b)=a+b;

(5)

则称S为拟带半环.

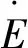
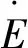
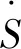
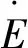
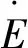
(i)S为拟群半环的分配格；

(ii)E为子半环；

证必要性，由引理2的证明可知，下证充分性.

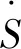
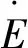
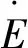
证必要性，由引理2的证明可得.

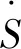
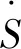
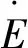
(i)S为完全Archimedean半环的分配格；

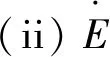
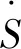
对于任意的c∈S,因为S为分配半环，所以

(6)

(7)

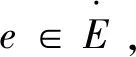
(8)