二维拟线性粘性波动方程的三层紧致差分格式

苏保金 姜子文

( 山东师范大学数学与统计学院,250358,济南 )

1 引 言

本文考虑如下的二维粘性波动方程

Dutt-BΔut-Δu+Aut=f(x,y,t,u),

其中,D,B,A是常系数,f为外力.

粘性波动方程描述了很多物理问题,如粘性介质中声波的传播,微尺度热量传播,流体中颗粒的随机移动等问题.目前,粘性波动方程的数值求解方法已经有不少,最具代表性的是差分方法和有限体积元方法,其目的都是建立适用于该问题的高效的数值求解格式.Dai[1]对于一维热传导方程给出了紧致差分格式.谢建强[2]则对一维粘性波动方程给出了一种三层紧致差分格式.Zhang J和Harfash A J[3,4]则针对类似的高维问题给出了高精度有限差分方法.王同科和高理平[5,6]则对二维问题分别给出了有限体积元和有限元方法.

本文通过Taylor展式得到二维拟线性粘性波动方程关于时间二阶的格式，再通过作用紧算子得到该方程关于空间四阶的紧致差分格式.数值实验验证了方法的精度和有效性.

2 格式构造

本文考虑如下的二维粘性波动方程的初边值问题

(1)

其中,Δ表示Laplace算子,Ω表示二维有界轴平行区域,∂Ω表示区域Ω的边界,T,D,B,A为正常数,u为待求函数,f,u0,u1为已知函数.

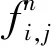
引入下列记号

在点(xi,yj,tn)处运用中心差分法离散时间导数,由Taylor展开可知

(2)

其中

在剖分网格上定义两个紧差分算子

则由Taylor展开可知

其中

在等式(2)两端同时作用算子Ax和Ay,且两个算子是可交换的,最终得到

(3)

其中

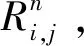
(4)

3 数值算例

本节将给出具体算例说明格式(4)的有效性.

例1系数A,B,D都取1，空间剖分步长hx=hy=h.精确解u=t10sin(πx)sin(πy),源项

f=(90t8+20π2t9+10t9+2π2t10)sin(πx)sin(πy)-(t10sin(πx)sin(πy))2+u2.

计算采用Matlab语言进行编程,Einf表示最大模误差,EL2表示离散的L2模误差.计算T=1时的空间收敛阶,计算结果如表1所示.

表1 T=1时，最大模误差与L2模误差

例2系数A=π2,B=2,D=2π2，空间剖分步长hx=hy=h.精确u=t5sin(πx)sin(πy),源项f=(40π2t3+20π2t4+2π2t5+5π2t4)sin(πx)sin(πy)-(t5sin(πx)sin(πy))2+u2.

计算采用Matlab语言进行编程,Einf表示最大模误差,EL2表示离散的L2模误差.计算T=1时的空间收敛阶,计算结果如表2所示.

表2 T=1时的空间收敛阶

我们从给出的数值算例可以看出,对于不同的空间步长，空间误差阶达到了四阶,证明了格式的有效性.我们通过数值算例也可以看出对于不同大小的常系数,格式是无条件稳定的.