圆锥曲线定点弦的一个有趣性质

广东省佛山市荣山中学

李燕高 (邮编：528000)

文[1]给出圆锥曲线焦点弦的一个有趣性质，笔者经过探索将其推广为一般圆锥曲线定点弦的性质，并发现由该性质可导出其它圆锥曲线的一些性质．

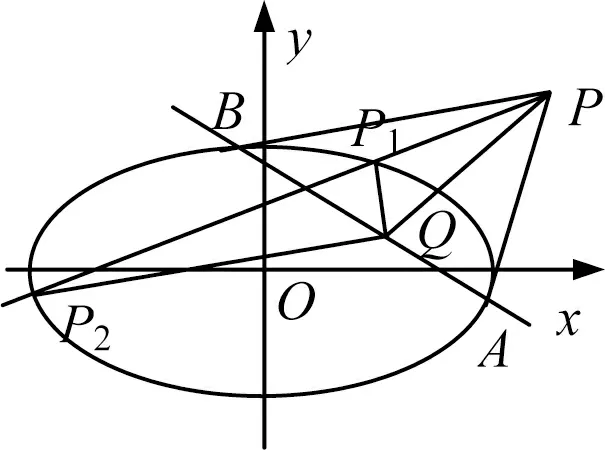
图1

定理1 如图1，给定圆锥曲线Γ：Ax2+Cy2+Dx+Ey+F=0，过曲线Γ外的定点P(m,n)作曲线Γ两条切线PA、PB，其切点为A、B，动点Q在直线AB上，过定点P的动直线交曲线Γ于P1、P2，记直线QP1、QP、QP2到直线AB的角分别为θ1、θ2、θ3，则cotθ1、cotθ2、cotθ3成等差数列．

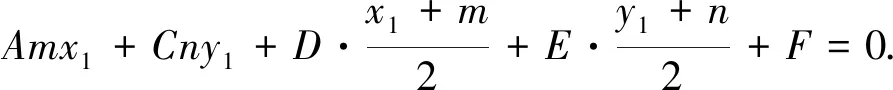
平移坐标系，使得坐标原点移到点P，则在新坐标系中，P(0,0)，二次曲线Γ：Ax2+Cy2+D1x+E1y+F1=0，直线AB：D1x+E1y+2F1=0(其中D1=2Am+D，E1=2Cn+E，F1=Am2+Cn2+Dm+En+F)；设P1(x3,y3)、P2(x4,y4)；

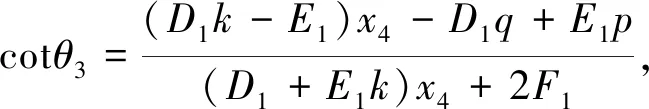
所以cotθ1+cotθ3=

故cotθ1+cotθ3=2cotθ2．

当直线P1P2垂直x轴时，可得cotθ1+cotθ3=2cotθ2．

所以定理1成立．

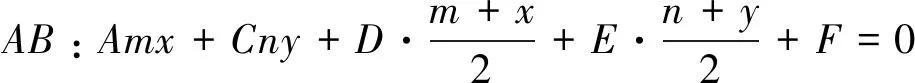
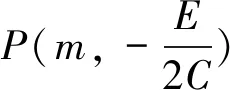
特别地，当点P为焦点时，推论1就是文[1]中的定理．

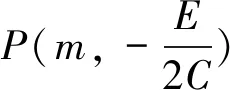
图2

在定理1及定理2中，如图2，过点P作直线AB(或l)的垂线，记垂足为T，当点Q与点T重合时，θ2=900，则cotθ1=-cotθ3，得θ1=-θ3，所以直线PT、直线TP1的夹角与直线PT、直线TP2的夹角相等．所以有：

当P在二次曲线Γ的对称轴上时，由推论3及二次曲线的对称性就可得文[2]、[3]、[4]的结论．