运动觅本质 变化提素养

浙江省平湖中学

李学军 (邮编：314000)

浙江省慈溪中学

苗孟义 (邮编：315323)

浙江省镇海中学

沈虎跃 (邮编：315200)

源起2018年11月26日，浙江省教育厅“百人千场”高中数学专家名师赴磐安县送教活动中，沈虎跃名师网络工作室学科带头人慈溪中学苗孟义老师在磐安二中开设了一节课题为《立体几何动态问题复习》高三一轮专题复习课，这节示范课使学生主动深入探究环境当中，在恰当的时机给学生创造自由飞翔的空间，有效地激发了学生的学习潜能，使得各种层次的学生都能够学有所获.苗老师的这节课设计朴实而有针对性，选题精炼而有代表性，在充分尊重学生的同时，又激发了学生对问题解决的热情，下面简要回顾课堂教学的部分环节以及自己的切身感受，谈一下自己对课堂教学的思考.

1 教师主导——驾驭课堂真老师

苗老师在知识复习阶段，回顾了余弦定理及余弦定理的变形，接下来从余弦定理出发，向平面向量过渡，通过平面向量公式的变形，逐步探究出本节课的主干知识，在这个探究的过程中，既要兼顾到教材概念、思想、方法的回顾，又要把相互关联的概念、思想和方法有机地串联起来，使学生能够达到真正意义的融汇贯通.

课堂实录1对角线向量定理的探究

师：余弦定理可以写成向量的形式吗？

师：两式相减，左边等于什么？

师：右边等于什么？

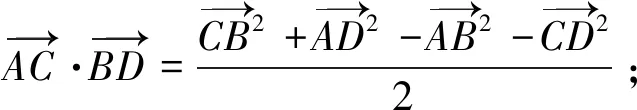
图1

师：同学们发现这个公式中字母的规律了吗？

生：由内及外再交叉相减.

师：这个定理就叫做对角线向量定理，有些书上也叫做四点向量定理；对角线向量定理，表明四边形的两条对角线对应向量的数量积可用四条边的长度表示.

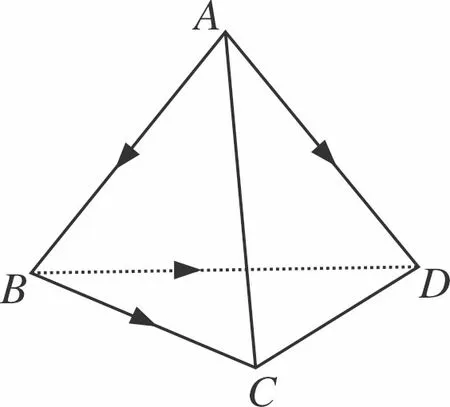
图2

师：今天我们研究的主要内容是立体几何中的动态问题，因此这个四边形要进行翻折，对不对？

师：假如我们以BD为轴进行翻折，这样平面问题转换为空间问题，同学们思考一下，在空间中，对角线向量定理是否成立？

生：在翻折的过程中，四条边的长度没有发生变化，因此在空间四边形中，对角线向量定理仍然成立；

感悟《普通高中数学课程标准(2017版)》中说“教师应理解不同数学学科素养水平的具体要求，不仅关注每节课的教学目标，更应关注主题、单元的教学目标，明晰这些目标对实现数学学科素养发展的贡献.”苗老师的这个环节从学生的最近发展区出发到知识理解，知识迁移，知识创新层层递进.真正体现了“整体设计必修和选择性必修课程的体系，处理好数学内容的层次性与数学学科核心素养水平发展的连续性”.在高三的一轮复习中从教材出发进行追本溯源，挖掘知识的本源，渗透必要的数学核心素养，这样的复习为后续的综合能力的提升奠定了非常扎实的基础.

2 学生主体——课堂掌控真主人

图3

A.存在某个位置，使得直线AC与直线BD垂直

B.存在某个位置，使得直线AB与直线CD垂直

C.存在某个位置，使得直线AD与直线BC垂直

D.对于任意位置，三对直线“AC与BD”，“AB与CD”，“AD与BC”均不垂直

课堂实录2对角线向量定理的理解

师：请同学们用自己所带的纸折一下，然后猜猜看或者用我们刚刚探究过的对角线向量定理.

(巡视和学生交流是猜的选项B，还是算出来的)

师：对于选项A如何判断？

师：对于选项B呢？

图4

师：最大值是多少呢？

师：最小值如何求呢？

生：当翻折后与A、B、D共面时最小.

师：如何求此时的AC′的长度呢？翻折后AC′与BD有什么关系呢？

师：在平时的学习中，我们要对每一个选项进行深究一下，选项C如何判断呢？

师：如果这种方法，在平时你一直在用，那么在大型考试中遇到这样类型的小题你就可以进行秒杀了.

感悟这个题目是2012年浙江高考数学理科的第10题，苗老师在课堂上引导学生动手折一折，实际上就是培养学生因地制宜，充分利用周围的环境解决问题，通过数学实验直观的发现答案.接下来苗老师“话风”一转，数学讲究严谨性，引导学生通过计算的方式进行严格推理论证.学生在苗老师的引导下，紧张有序的进行逐个选项的论证.虽然这是高三的一轮复习，但是苗老师在课堂上给学生留出足够的时间，让学生对所学习的知识进行去思，去悟，去用，真正实现了学以致用.

3 课堂主场——渗透素养真领地

图5

课堂实录3对角线向量定理的内化

图6

生：∠ACD=∠BCD，

师：请问，cos∠BCD等于多少？

生：cos∠BCD=cos2∠ACD=

师：在平面四边形ABCD中，你会求BD的长度吗？

师：当点D在什么位置时，BD的长度最小？

生：当点D′落在BC的三等分点E处时BD′=3-1=2最小.

感悟《普通高中数学课程标准(2017版)》中提出“数学学科素养包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析.这些数学核心素养既相对独立、又相互交融，是一个有机的整体.”在标准中还给出了核心素养的水平划分的三个层次具体的要求，因此在课堂教学中，苗老师根据学生的现有的学习能力，引导学生主动地参与学习，培养学生用数学思维和习惯进行学习，通过较为复杂的数据运算，取值范围的求解，翻折过程中的动态变化，使得数学运算，逻辑推理，直观想象等数学核心素养有效扎实地落到实处.

图7

4 问题主线——能力提升真效果

例3(2015年浙江省普通高中学业水平考试数学试题18题)如图，在菱形ABCD中，∠BAD=60o，线段AD、BD的中点分别为E、F，现将△ABD沿对角线BD翻折，则异面直线BE与CF所成角的取值范围是( )

图8

课堂实录4一类问题的多种思维

师：这是一个选择题，你有没有办法猜出答案呢？

师：通过特殊值法进行定性分析是有风险的，如果题目中有陷阱就比较麻烦，接下来，我们进行定量计算，不妨设菱形ABCD的边长为2.

师：非常棒！事实上当△ABD沿对角线BD翻折的过程中，点E的轨迹是是什么？

生：是一个圆.

师：线段BE在翻折的过程中的轨迹是什么？

生：是圆锥的侧面.

师：请同学们课后思考一下，你可以通过这样的思路解决这道题吗？

教学启示

图9

(1)关注教材的潜力

数学选修2-1第106页例2如图，甲站在水库底面上的点A处，乙站在水坝斜面上的点B处.从A、B到直线l(库底与水坝的交线)的距离AC和BD分别为a和b，CD的长为c，AB的长为d.求库底与水坝所成二面角的余弦值.

在解决这个问题我们可以从三个层次进行探究.

第三层次：再推广一下当AC，BD与CD不垂直时，

正如叶圣陶先生所说：“教材无非是个例子，它只能作为教课的依据.要教得好，使学生受益，还要靠教师善于运用.”事实上在我们的教材中，只要我们做个有心人，用心去挖掘这样的素材，一定可以从不同角度得出更多有意义的结论，使得我们课堂更加韵味无穷.

(2)关注专题的实效

对角线向量定理，可以快速解决一类关于向量数量积或向量夹角问题，但并不是一味追求高难度的解题技巧，恰恰相反，通过这种专题的探究，寻求一类问题的通解通法，进而形成一类问题的统一解法.事实上对于动点的轨迹问题苗老师的这节课完全可以设计动画演示，通过动画学生对动点的运动状态理解可能会更加深刻，尤其对空间想象能力不强的学生来说效果会更好.但是高三复习目的是让学生在考场上能够在有效的时间内对所考查的问题进行有效解决，因此在高三的复习课堂就应该为这样的目的进行设计和实施.

(3)关注考题的联系

考题1(2014年1月浙江省普通高中学业水平考试第25题)如图，在Rt△ABC中，AC=1,BC=x，D是斜边AB的中点，将△BCD沿直线CD翻折，若在翻折的过程中存在某一时刻，使得CB⊥AD，则x的取值范围是( )

图10

图11

图12

考题2(2009浙江高考理科第17题)如图，在长方形ABCD中，AB=2,BC=1，E为DC的中点，F为线段EC(端点除外)上的一动点.现将△AFD沿AF折起，使平面ABD⊥平面ABC，在平面ABD内过点D作DK⊥AB，K为垂足.设AK=t，则t的取值范围是.

这样背景的试题在高三的复习资料中会经常出现，在解决问题的过程中，我们也应该关注这些试题之间是否存在共性的东西，解决这类问题是否有行之有效的共性办法，这也就是数学中的合情推理和演绎推理的最好落实.正如波利亚曾形象地指出“好问题同某些蘑菇有些相似，它们大都成堆地生长，找到一个之后，你应当在周围再找一找，很可能就有几个”.

总之，数学教学不仅要教授数学知识，数学方法，更要引导学生把握数学内容的本质，发展学生的数学核心素养，用数学的眼光看问题.张奠宙教授曾经说过：“数学教学的有效性关键在于对数学本质的把握、揭示和体验.”在教学中要想更好的驾驭时刻在变化的课堂，就需要老师在平时不断提升自身的数学素养，从而实现真正意义的教学相长.