数控机床轴承-主轴系统热态特性分析

郑龙燕

（山东冶金技师学院 济南 250109）

高速切削技术的发展，对机械加工精度提出更高的要求。机械加工中的加工精度受到“机床-夹具-刀具-工件”工艺系统各个环节热变形的影响。英国伯明翰大学的 J.Peclenik[1-2]调查表明，热变形已成为影响机床加工精度的首要因素，占机床总误差的40%～70%。因此，控制机床加工精度的关键在于控制关键部件的热变形。

轴承-主轴系统是机床的重要组件，轴承运转过程中的摩擦生热会使主轴产生热变形，影响机床的加工精度。本文以某型号数控车床轴承-主轴系统为例建立有限元模型，进行发热量和热边界条件的计算。利用有限元软件ANSYS对其进行温度场仿真，理论计算了主轴系统的温升和热变形，并通过搭建轴承-主轴系统热伸长试验台，进行实验验证。

1 轴承-主轴系统有限元模型

依据通用有限元分析流程，在三维软件Solidworks 中建立几何模型，并对其进行以下简化处理：

(1)删除螺纹孔、油管、注油孔等细小特征；

(2)删除倒角和圆角；

(3)利用简单结构的实体模型代替复杂结构的部件，比如；用简单圆环来代替主轴冷却套；

(4)在保证整体结构不变的情况下，可修改各模型的尺寸，保证各零件装配正确。

通过对几何模型进行简化，可提高网格划分的质量，节约仿真计算的时间，将简化后的三维模型导入 ANSYS，如图1所示。对轴承-主轴系统各部件的材料属性进行设置，将主轴材料设定为38CrMoAlA，轴承材料设定为 GCr15，其余零件设定为45 号钢。

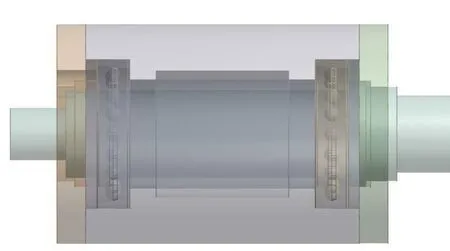
图1 轴承-主轴系统示意图

对简化的轴承-主轴系统展开网格划分的过程，网格划分过粗会降低计算精度，划分过细会增加计算时间，而且不同的网格划分方法会影响网格的优劣，因此，需要根据主轴零件的几何尺寸选择合理的网格单元尺寸，主轴部件的尺寸在几毫米到几百毫米，选择网格尺寸为1～10 mm，对简化后的轴承-主轴系统采用自动网格划分，如图2所示。

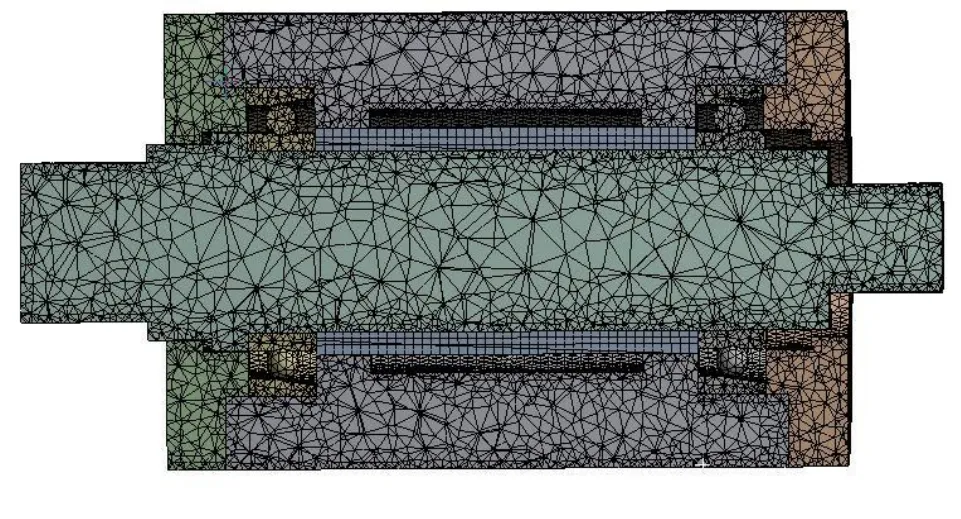
图2 轴承-主轴系统网格划分

2 热载荷及边界条件计算

2.1 热载荷计算

轴承-主轴系统高速运转时，其内部轴承因接触摩擦而产生大量的热，其发热主要与轴承的摩擦力矩有关，Palmgren[3]推导出发热量和摩擦力矩的关系式：Nr=1.05×104Mn。

轴承的摩擦力矩主要由以下三部分构成：润滑剂粘性摩擦力矩M0、载荷引起摩擦力矩M1和轴承自旋摩擦力矩M2。

1）润滑剂粘性摩擦力矩

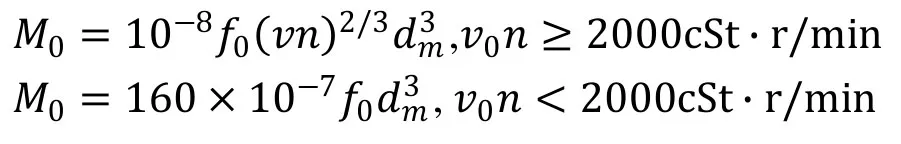
2）载荷引起的摩擦力矩

M1=f1P1dm

3）自旋摩擦力矩

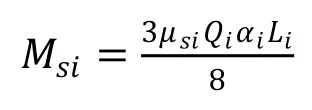
式中：f0是与润滑有关的系数，油雾润滑取1；ν为运动温度下的润滑油粘度；f1为轴承类型和载荷有关的系数； μ 为球与滚道接触区的摩擦因数；Q为球与滚道的法向接触载荷(N)； α为球与滚道椭圆接触长半轴 (mm)； L为第二类椭圆积分。

2.2 对流换热系数计算

对流是指因为流体的运动，使流体各部分间发生相对位移，冷热流体相互掺混所产生的热量传递过程。对流换热系数[4]是指流体与固体表面之间的换热能力，即物体表面与附近空气温差 1℃，单位时间单位面积上通过对流与附近空气交换的热量。

1）轴承座表面热对流换热系数

轴承座的热对流参数指静止轴承座表面与空气的自然对流换热系数，经验值取9.7 W m2∙℃

2）旋转轴表面与空气的对流换热系数

轴承在实际运转过程中，产生的部分热量通过热传导的方式传递给主轴，主轴在旋转过程中与周围空气产生热量交换，这种交换方式属于强迫对流换热，可以通过下式得到：

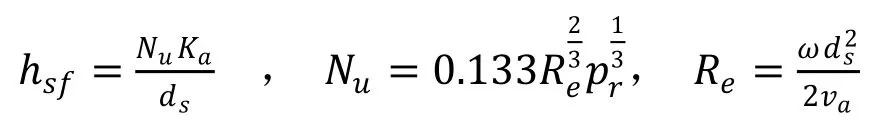
式中：ℎsf是对流换热系数(W∙m-2∙℃-1)； Nu为努谢尔特数；Ka为主轴的热传导系数 W∙m-1∙℃-1； ds为主轴直径(m)；Re为而诶雷诺数；Pr为普朗特数；ω 为主轴旋转角速度(rad∙s-1)； 空气的运动粘度(m-2s-1)； 相应流体的运动粘度(m-2s-1)； 相应流体的密度(kg∙m-3)； v 为相应流体的等压比热容； K为相应流体的热传导系数（W∙m-1∙℃-1）。

3）轴承组件与润滑剂的对流换热

轴承在使用时需要添加润滑剂以减小摩擦，运转过程中，内部组件与润滑剂之间存在热量传递现象，这种热量传递属于强迫对流换热，Harris[5]推荐轴承组件与润滑剂间产生的强迫对流换热系数为：

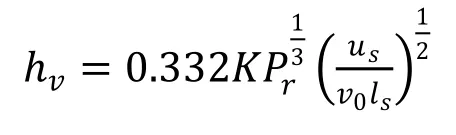
式中：K 为润滑剂导热系数(W∙m-1∙℃-1)；us为冷却表面与润滑剂间相对速度(m∙s-1)； ls为特征长度(m)；v0为润滑油粘度（Pa∙s）。

对于滚动体表面与润滑油之间的强迫对流换热，式中us取保持架的表面速度，ls为滚道节圆直径。对于内、外圈滚道表面与润滑油之间的强迫对流换热，则us取保持架表面速度的三分之一。

不同转速下的有限元模型边界条件如表1所示，以转速10 000 r/min为例，分析该转速下，轴承-主轴系统的温度场分布情况。

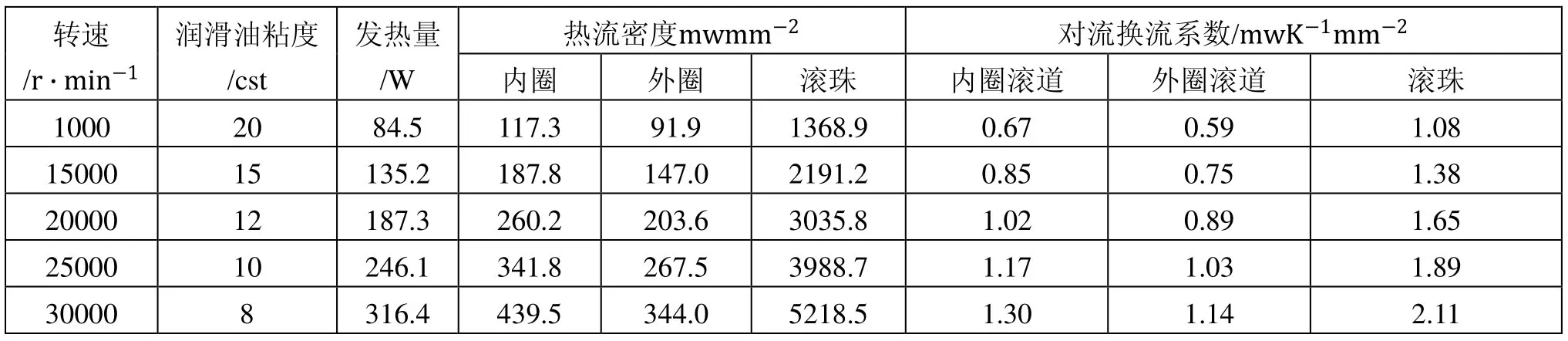
表1 轴承有限元模型边界条件计算值

3 轴承-主轴系统热态特性分析

3.1 轴承-主轴系统温度场分析

图3是转速10 000 r/min 时，该轴承-主轴系统连续运转达到热平衡时的温度场仿真结果，图 4 ～图6是各组件温度分布。可以看出，轴承座温度最高为36.5℃，主轴最高温度为40.05℃，轴承-主轴系统中最高温度为 43.05℃，该最高温度发生于左侧轴承中内圈滚道与滚动体接触的部位。

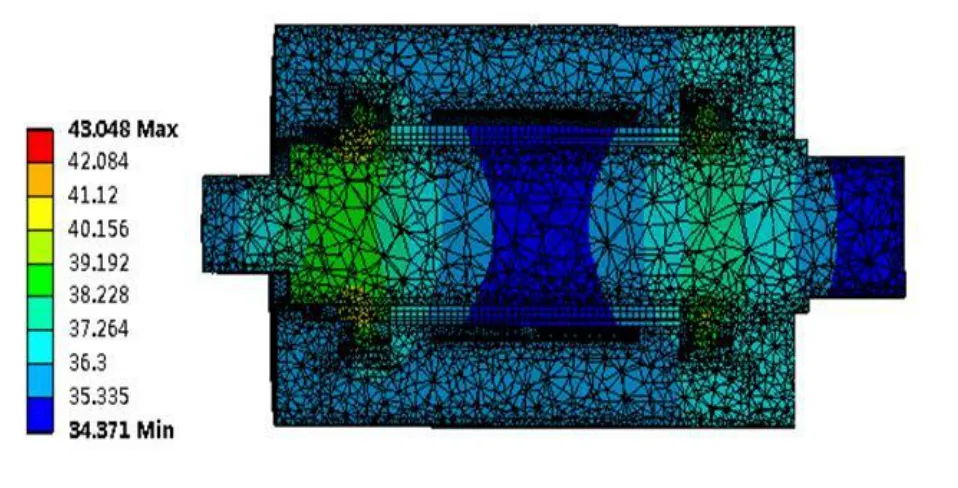
图3 轴承-主轴系统整体温度场

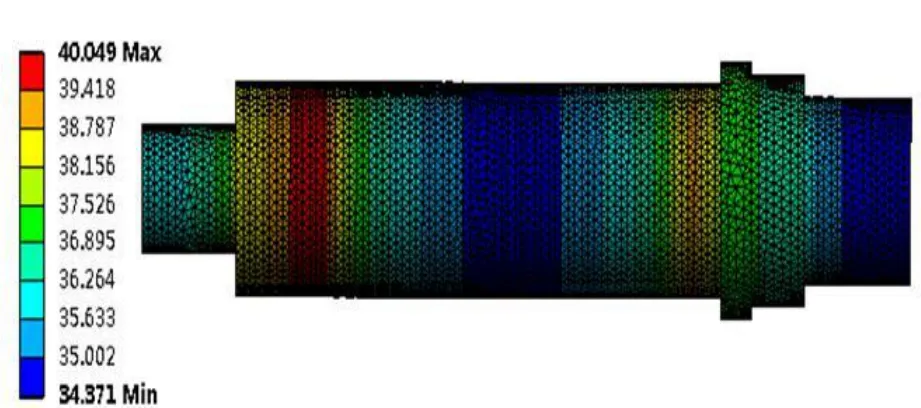
图4 主轴温度场

图5 轴承座温度场

图6 轴承温度场

3.2 主轴热变形分析

在轴承-主轴温度场仿真模型的基础上，展开热力耦合分析，建立轴承-主轴热伸长模型，计算主轴热伸长。对轴承-主轴系统温度仿真分析结果进行后处理，把主轴的温度场数据导入主轴的热伸长模型中，并给主轴施加转速边界条件，给轴承座施加固定约束条件，求解主轴的热伸长。

图7是转速10 000 r/min时主轴达到热平衡后的主轴的热变形云图，由图中可以看出稳态时，主轴单端端面热伸长（X向）最大为12.587μm，而Y方向和Z方向主轴的热变形最大分别为 4.1557μm和 4.131μm。与径向热变形相比，主轴轴向热伸长更为严重。建立计算主轴热伸长的仿真模型时，主轴左右端面均未固定，处于自由状态，因此，该主轴的实际热伸长为右端面热伸长数据与左端面热伸长绝对值求和，可到主轴在10 000 r/min时，轴向热伸长为ΔL ，如式：

ΔL=L++L-=12.587+9.994=22.581 um

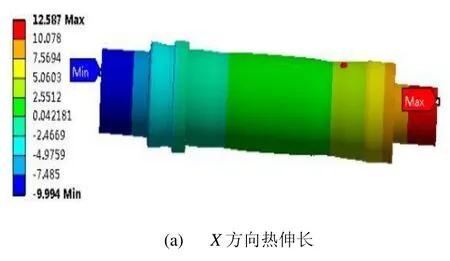
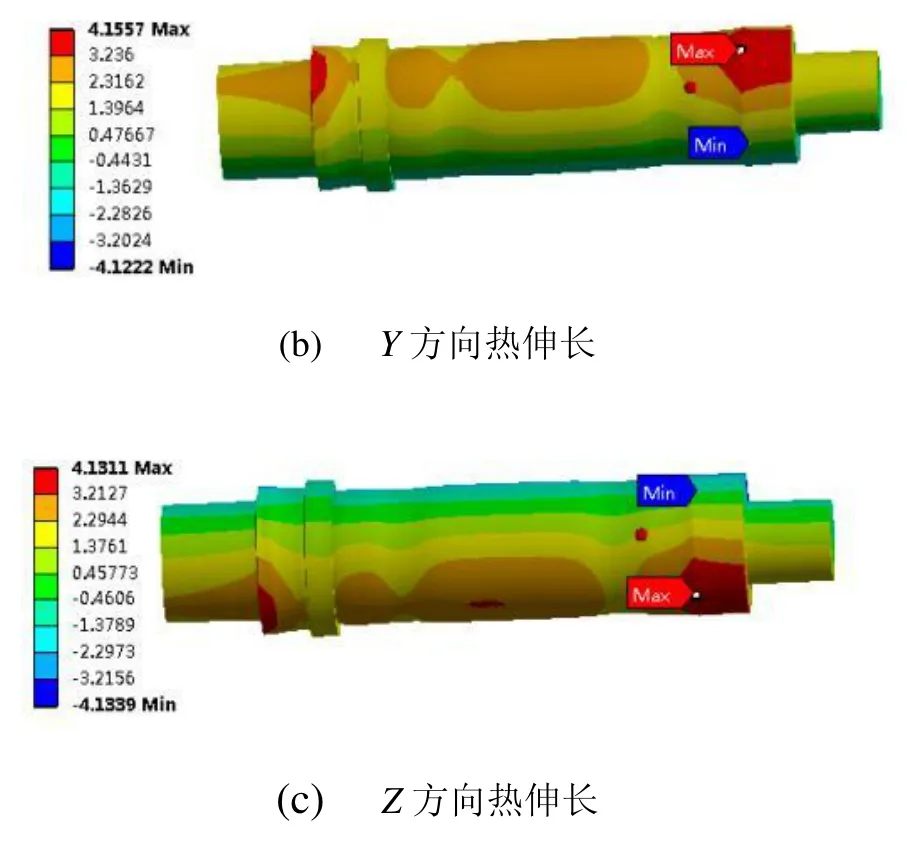
图7 主轴热伸长

4 轴承-主轴系统热伸长试验验证

搭建高精度轴承-主轴系统热伸长测试实验台，如图8所示。高精度激光位移传感器用磁力表座固定于实验台表面上，其测试精度为0.1 μm，通过主轴端面位移来测试主轴轴向热伸长。由于高精度激光位移传感器固定于实验台表面，因此，其测出的热伸长为主轴绝对热伸长。

图8 轴承-主轴系统热伸长测试实验台

图9为主轴转速为10 000 r/min时，3h内主轴热伸长数据，图中黑线是原始信号，红色是趋势项，对实验原始信号进行趋势项处理，发现热伸长数据先上升后缓慢下降趋于平稳的现象。实验在0时刻，高精度激光位移传感器的数值为0.05151 mm，实验结束时刻，高精度激光位移传感器的示数为0.0725 mm，因此计算出实验测得的主轴轴向热伸长的数据为。

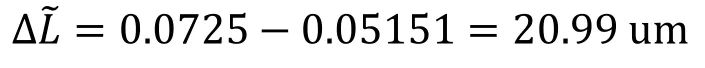
有限元方法计算的主轴热伸长为ΔL ，实验测试的主轴热伸长为计算值与实验值的相对误差ε：

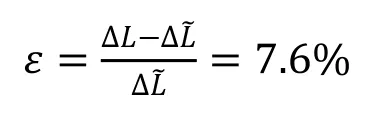
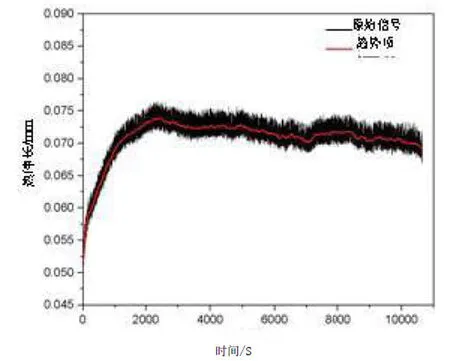
图9 实验主轴热伸长的原始信号及趋势项

5 结语

通过对轴承-主轴系统的分析计算理论值以及主轴热伸长测试的实验值，表明有限元模型计算的正确性。轴承-主轴系统的温度场表明，主轴左侧轴承的温度较高，在运转的过程中产生较大温升，温度的变化会导致主轴发生一定的热变形，影响高速机床工作时所达到的加工精度。

在后续的仿真计算中，可以考虑改变润滑条件、冷却条件，选用合适的轴承支撑系统、误差补偿等方式降低主轴温升，控制主轴变形量，改善高速数控机床的加工精度。