线性模型的海基制导系统误差分离方法性能分析

周萱影，王正明，李 冬，王炯琦

(1. 国防科技大学 文理学院， 湖南 长沙 410073； 2. 国防科技大学 前沿交叉学科学院， 湖南 长沙 410073；3. 中国人民解放军91550部队， 辽宁 大连 116023)

在远程导弹进行精确打击时，惯性器件误差是影响导弹打击精度的重要因素之一。在飞行器精度鉴定过程中，由于经济成本限制，只能进行少量特殊弹道的飞行试验，并利用遥测与外测数据，分离出特殊弹道的制导系统误差，将其造成的落点偏差折算到最大射程弹道上，进而获得全程弹道的命中精度[1]。实际上，对于导弹的落点偏差，制导系统误差引起的落点偏差是总落点偏差的主要因素之一[2]。

对于陆基导弹来说，制导系统误差主要为制导工具误差。然而，对于发射平台是海基的惯性导弹来说，除了与陆基导弹共有的制导工具系统误差之外，潜射导弹的系统误差还包括由移动发射原点造成的原点定位、定向、定速以及平台调平等初始误差[3]，因此，海基导弹的制导工具系统误差分离问题要比陆基导弹复杂。提高制导系统误差分离精度的关键是针对各项误差源的物理特性，建立误差模型，设计合理的参数估计策略以及合适的参数估计方法。

传统的制导工具系统误差估计方法的基础是对速度域上的线性回归模型[4]进行整体估计，主要方法有最小二乘估计方法、Bayes估计方法、主成分估计方法(Principal Component Analysis，PCA)[5-6]、正则化分析方法[7]等；此外，文献[8]给出了基于动力系统求解的制导误差分离方法。以上研究均是基于陆基情况下的误差估计方法，文献[9]建立了关于海基导弹初始误差分离的线性模型，将初始误差与工具误差进行了线性分离。由于海基导弹存在的初始误差与制导工具误差相互耦合，使得误差模型具有较大的病态性。

为了对比分析海基惯性导弹背景下不同制导工具系统误差分离策略的差异，本文从线性模型下陆基制导工具误差分离方法入手，针对海基制导工具误差的主要误差源[3]，分析了Bayes估计、主成分估计以及正则化分析的优缺点，提出了适合于海基制导工具误差分离的整体、分段以及迭代等分离策略。

1 线性分离模型及参数估计方法

传统的制导工具误差分离线性模型为[4-8]：

(1)

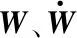
实际应用中，由于待分离的误差系数C较多，环境函数矩阵Sm×n的复共线性，传统最小二乘估计性能较差，通常采用相应的改进误差分离方法，包括结合待分离误差系数先验信息的Bayes估计[10-11]、主成分优选的主成分估计[5,12-13]，以及结合误差分离系数稀疏约束的正则化估计[7]。

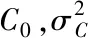
表1 几种估计方法比较

2 海基制导工具系统误差分离策略

海基导弹的制导误差包括制导工具误差、由移动发射原点引起的初始状态误差。海基惯性制导导弹的初始误差实际上和工具误差一样，与总体系统误差之间的关系是线性的[9]，因此可以将总体系统误差分成初始误差与工具误差两类进行分离，这样可以降低由初始误差与工具误差之间的耦合性引起的模型病态性，从而提高误差分离精度。

本文根据导弹初始误差与工具误差的不同性质，提出了整体估计、分段估计以及迭代估计的三种误差估计策略。

将式(1)改写成如下形式：

ΔW=ΔWinitial+ΔWtool=S0C0+S1C1+ε

(2)

其中：ΔWinitial,ΔWtool∈Rm×1分别为海基导弹特有的初始误差部分以及与陆基相同的制导工具系统误差部分；C0∈Rn0×1,C1∈Rn1×1为待估计的初始误差系数和工具误差系数；n0,n1为待估计的初始误差项数和工具误差项数；S0∈Rm×n0为初始误差的环境函数矩阵，S1∈Rm×n1为工具误差的环境函数矩阵。

2.1 整体估计策略

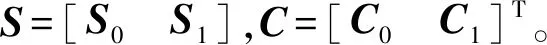
实际上，由于制导系统误差模型较大，且部分误差项之间的耦合关系严重，在3.1节的仿真部分，其环境函数矩阵S的条件数高达1035，最小特征值为10-18。而由

(3)

以及参数估计的相关理论[14-15]可知，小特征值会引起矩阵的病态性。当矩阵病态性很强时，参数估计的结果会缺少数值稳定性，即输入数据中极小的扰动也会引起输出结果很大的变动。因此，除了对参数估计方法的改进以外，还应设法降低环境函数矩阵的病态性。

本文提出通过减少环境函数矩阵S维度的方法来减弱模型的病态性。由此，针对工具误差以及初始误差的特性，提出了以下两种估计策略：分段估计策略以及迭代估计策略。

2.2 分段估计策略

针对海基制导系统误差含有初始误差的特性，以及初始误差与工具误差之间耦合性而引起的病态性，分段估计策略给出以下假设：

假设1：初始段测量数据ΔW0=ΔWm0×1⊂ΔWm×1中只含有初始误差ΔWinitial，即ΔW0=ΔWinitial，且后段中初始误差的值始终保持不变。

在此假设下，首先将系统误差ΔW根据时间分成前段系统误差ΔW0∈Rm0×1和后段系统误差ΔW1∈R(m-m0)×1，其中数据节点m0通常根据实际背景选取，并根据相应误差系数的环境函数矩阵S0、S1，分别对C0、C1进行估计。

具体的步骤如下：

Step1：设置初始段与后段数据分界点m0；

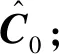
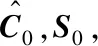
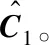
分段估计策略的合理性在于海基导弹发射初期，由发射原点造成的初始误差比重相对制导工具误差较大，故可以忽略初段数据中的制导工具误差，先对初始误差进行分离；再将后段测量数据中的初始误差扣除后，得到剩余的制导工具误差；此时，再对工具误差进行估计则能得到更准确的误差分离结果。

2.3 迭代估计策略

分段估计结果的合理性是建立在假设1的前提下。但实际上，在海基导弹的发射初期存在制导工具系统误差，且移动发射原点造成的初始误差并非常值，而是随时间变化的。因此，迭代估计策略在分段估计的基础上进行了改进，通过对测量数据中的初始误差与工具误差进行迭代分离，以此得到收敛后准确的误差系数估计。

具体步骤如下：

Step1：设置迭代终止条件δ，以及最大迭代次数N；

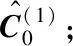
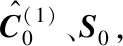
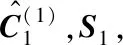
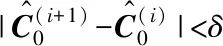
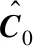
3 仿真算例

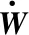
制导工具系统误差估计的线性分离方法是在假设2的前提下，在模型(2)的基础上进行的。

3.1 仿真条件

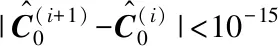
基于对算例中的环境函数进行相关性分析，在初始误差中，与过载无关的三个方向初始平台角偏差Φ0x、Φ0y、Φ0z与经度λ0、纬度B0、高程h0具有很强的耦合性，因此本文主要对21项工具误差系数以及包括三个方向的初始速度v0x、v0y、v0z和经度λ0、纬度B0、高程h0在内的6项海基初始误差系数进行系统建模与仿真估计。

3.2 仿真结果

本小节中给出了27项制导工具系统误差系数在不同策略下的Bayes估计、主成分分析、正则化分析三种方法的估计结果，并给出了方差3σ准则以及弹道差3σ准则两种评价标准下的具体估计结果，这两种评价标准即是从待估参数C层面以及待估信号SC层面对误差分离方法以及误差分离策略进行分析与评定，具体结果如下。

3.2.1 方差3σ准则

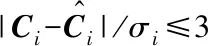
具体地，表2～4分别给出了整体估计策略、分段估计策略以及迭代估计策略下三种估计方法的全部27项方差结果，其中，加粗项为3σ标准内的对应项，第1～21项为制导工具误差系数，第22～27项为初始误差项。

从表2中可以看出，对于整体估计策略，Bayes估计方法共分离出11项误差，其中5项为制导工具误差，其余6项初始误差均可估计；而PCA方法共分离出4项系统误差，全部为初始误差，正则化方法共分离出6项误差，其中1项为制导工具误差，其余5项为初始误差。

从表3中可以看出，对于分段估计策略，Bayes估计方法共可分离27项系统误差中的26项，其中20项为制导工具误差，6项初始误差均可估计；而PCA方法以及正则化方法分别分离出8项系统误差，且全部方法均能分离出6项初始误差。

从表4中可以看出，对于迭代估计策略，Bayes估计方法可分离出全部27项误差，而PCA方法以及正则化估计方法在分段估计策略的误差分离结果基础上，又分离出了第1项以及第9项制导工具误差。

3.2.2 弹道差3σ准则

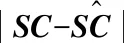
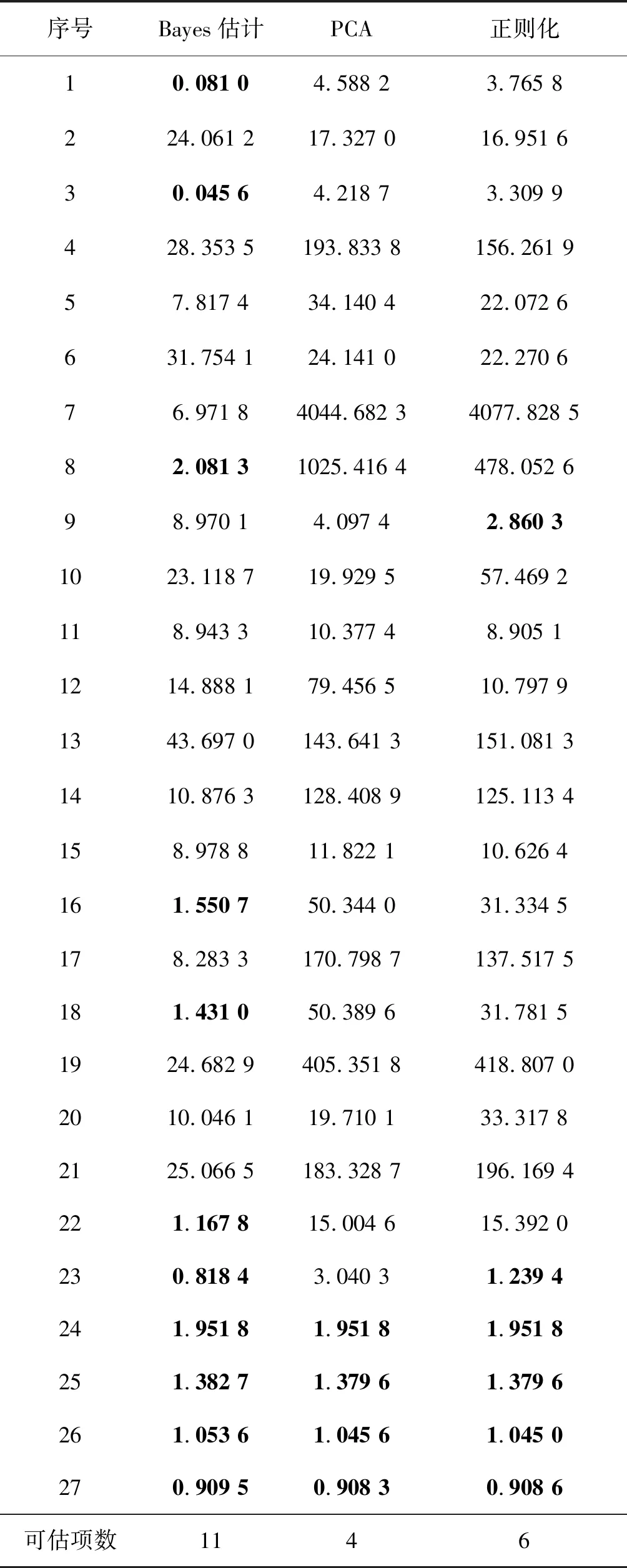
表2 整体估计策略下三种方法的方差结果

实际上，在本次仿真背景中，弹道X方向的弹道误差对于落点偏差来说是最主要的影响因素。因此，在弹道差标准下，本文分别给出了三种估计策略下X方向弹道差。

表3 分段估计策略下三种方法的方差结果

为了准确地对三种估计策略的误差分离效果进行评价，图1～3首先给出了三种方法下的弹道差，其中Bayes、PCA和R分别表示Bayes估计、主成分分析方法以及正则化方法。由图2、图3可以看出，在整体估计策略下，三种方法的弹道差

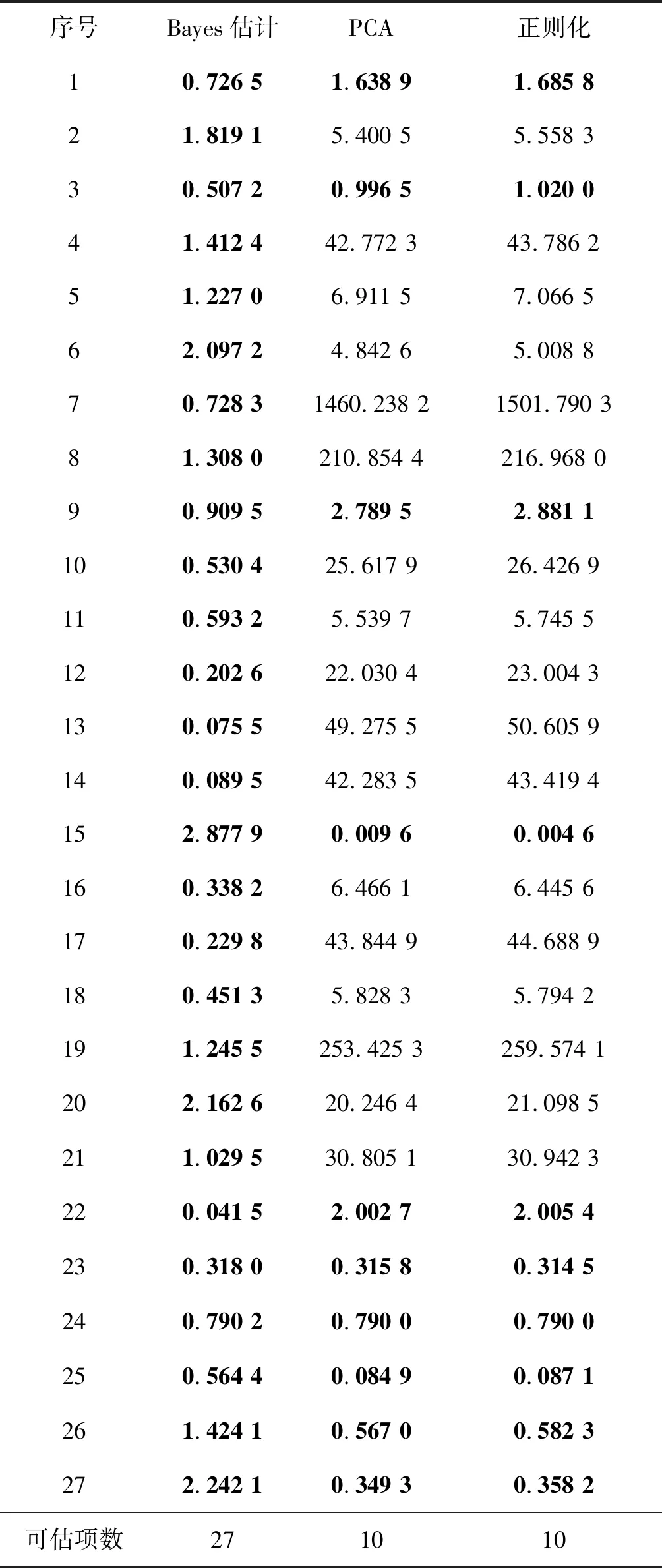
表4 迭代估计策略下三种方法的方差结果

相差不大，均在30 s左右以后才满足3σ标准。而在采用分段策略以及迭代策略时，主成分分析与正则化估计方法的弹道误差均有了明显的降低，且由于这两种方法之间的精度差别极小(仅10-7～106m/s)，因此两者的弹道差曲线在图示区域内几乎重叠。

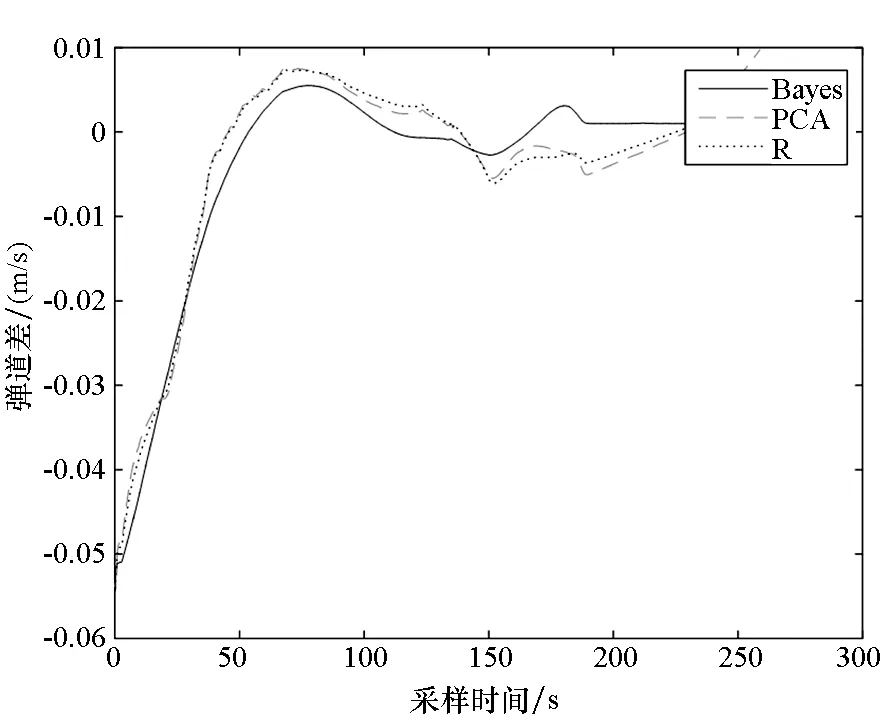
图1 整体估计下的X方向弹道差Fig.1 Difference value of trajectory of the total strategy at X direction

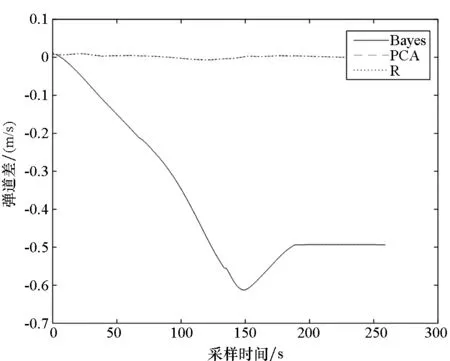
图2 分段估计下的X方向弹道差Fig.2 Difference value of trajectory of the piecewise strategy at X direction

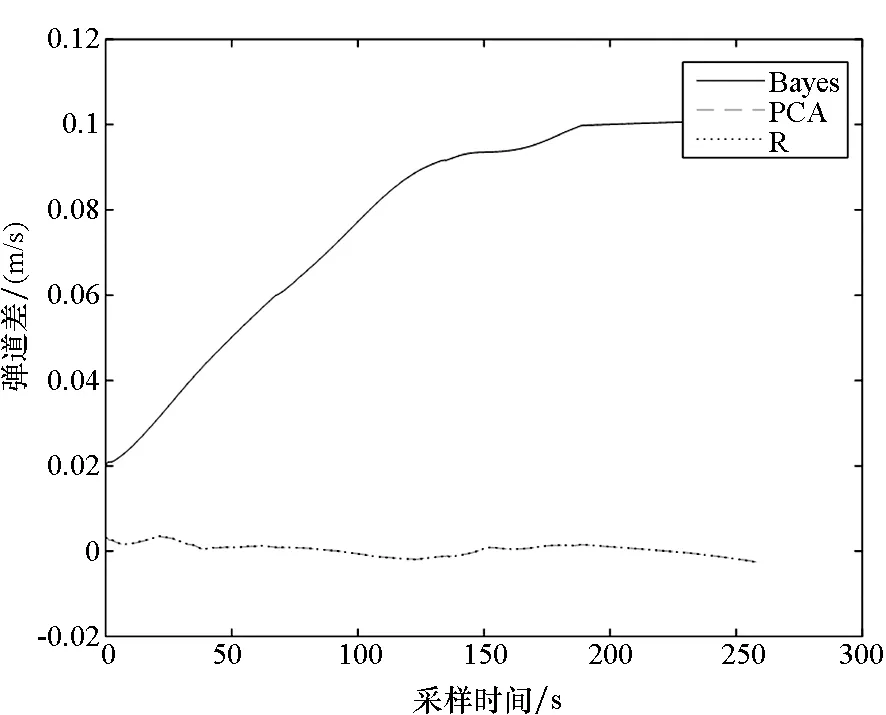
图3 迭代估计下的X方向弹道差Fig.3 Difference value of trajectory of the iteration strategy at X direction

为了更好地观察并分析仿真结果，图4～6单独给出了正则化方法下的三种参数估计策略弹道误差结果。可以看到，分段估计策略及迭代估计策略的弹道误差始终在3σ范围之内，并且迭代估计策略得到的弹道误差结果比分段估计策略得到的结果也有进一步的改善。

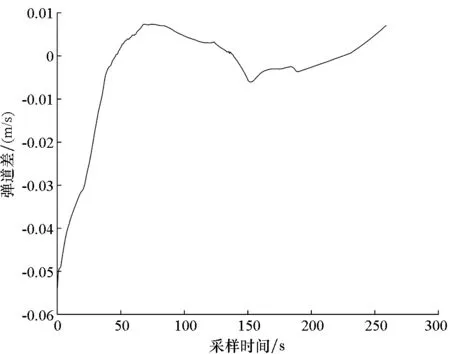
图4 整体估计下正则化估计的X方向弹道差Fig.4 Difference value of trajectory of the total strategy at X direction

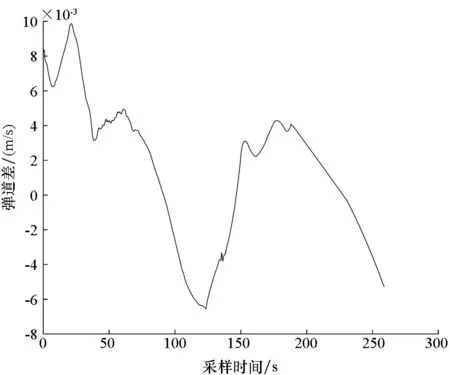
图5 分段估计下正则化估计的X方向弹道差Fig.5 Difference value of trajectory of the piecewise strategy at X direction

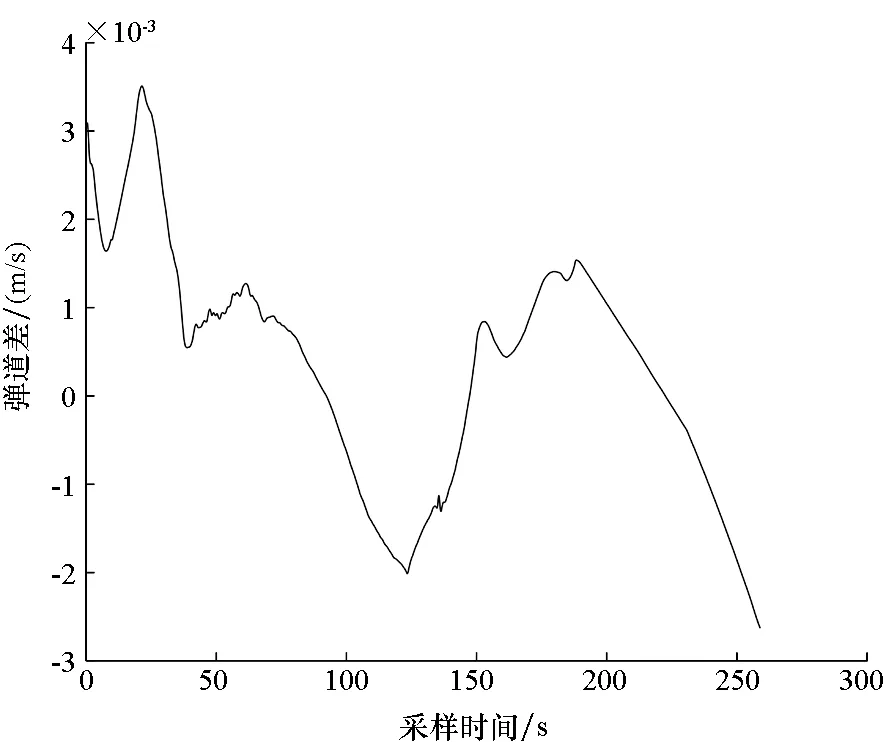
图6 迭代估计下正则化估计的X方向弹道差Fig.6 Difference value of trajectory of the iteration strategy at X direction

3.3 结果分析

通过以上仿真计算的结果，得到如下结论。

3.3.1 估计方法评定

1)通过方差3σ准则的评价结果，可以看到在三种估计方法中，Bayes估计方法分离出的制导系统误差系数是最多的。这说明，在先验信息准确的情况下，Bayes方法具有最优的参数估计结果；

2)主成分分析与正则化方法所分离出的误差系数结果差异不明显，造成这一现象的原因是由于这两种方法的基本思想原理是一致的，均为广义岭估计；

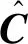
4)虽然在弹道误差标准下，Bayes方法结果较差，但由于迭代估计策略逐步将工具误差与初始误差分离出来，使得迭代策略下Bayes估计结果比分段策略下的结果有了显著的提高，这也说明了迭代策略在改善模型病态性上有较强的效果。

3.3.2 估计策略评定

1)通过方差3σ准则，从表2～4可以看出，整体估计策略下，Bayes方法仅能估计出11项，而分段估计策略下，Bayes方法能估计出27项中的26项，且迭代估计策略下，Bayes估计方法能估计出全部27项误差系数，这说明通过减少环境函数矩阵间的相关性，逐步分离出工具误差与初始误差，能较大程度上提高估计结果的精度；

2)从主成分分析方法以及正则化估计方法来看，利用分段估计策略得到的误差分离项数结果相比传统的整体估计策略，也有显著的增加，且迭代估计策略也在一定程度上优于分段估计；

3)从三种估计策略的弹道残差图来看，迭代估计策略与分段估计策略在弹道差上均减小了一个量级，明显优于传统的整体估计策略；无论在弹道差3σ标准下或是方差3σ标准下，迭代估计的结果都要优于分段估计结果，这是由于迭代估计策略通过不断的迭代过程将初始误差与工具误差逐步分离，从而能更精确地利用先验信息进行参数估计。

4 结论

本文以海基惯性制导导弹为背景，在制导工具系统误差线性分离模型的基础上，考虑到误差模型中环境函数矩阵的病态性，采用了Bayes估计方法、主成分分析方法以及正则化分析方法对误差系数进行估计；针对海基特有的制导系统初始误差，提出了整体估计策略、分段估计策略以及迭代估计策略，并进行了数值的仿真计算。结果表明，在弹道误差最小的条件下，主成分分析及正则化估计方法结果较好，并且分段估计策略和迭代估计策略的结果比传统的整体估计效果要好，这一结果证实了本文针对海态数据特性建立的对制导工具系统误差分离策略的合理性与可行性。