基于Kullback-Leibler距离离散度的加权代理模型

晏 良，段晓君，刘博文，徐 琎

(国防科技大学 文理学院， 湖南 长沙 410073)

在工程研究中，利用计算机通过仿真试验可对真实复杂系统进行高精度的模拟，从而分析该系统的相关特性[1]。然而，单次高精度仿真试验通常面临计算效率低、时间成本大等问题，因此诸如可靠性评估、失效概率验证等需要大规模仿真的任务在实际操作中很难完成。代理模型由于其计算复杂度低、数学表达明晰等特点，在计算机仿真试验中得到了广泛应用[2-3]。实际上，代理模型重点关注输入和输出之间的数学关系。给定试验设计及观测数据，代理模型通过回归或插值等方法拟合观测数据，可给出相应的预测均值、方差等统计量。

常用的代理模型构造方法有很多，例如：多项式响应曲面(Polynomial Response Surface, PRS)[4]、多元自适应回归样条(Multivariate Adaptive Regression Splines, MARS)[5]、高斯过程(Gaussian Process, GP)[6]，等等。针对不同的模型特点(如光滑、线性、非线性)和数据特征(噪声、异常值)，通常会选用不同的代理模型。

事实上，除了以上文献所提供的经验，基于一些准则可以对代理模型进行筛选。经典的模型选择准则[7]包括：基于拟合优度(Goodness of Fit, GoF)、基于预测误差(Prediction Error, PE)或者模型误差(Model Error, ME)、基于概率分布距离(Distributional Discrepancy, DD)、基于后验概率(Posterior Probability, PP)等。然而，基于上述准则需要对每类候选模型进行计算，会增加较多的计算量；另外，从所有候选模型中仅挑选单个最优模型，不考虑其他模型也在一定程度上造成了信息的浪费。出于上述考虑，一些研究[8-10]也侧重于利用所有的候选模型，即构造加权代理模型。

此外，构造加权代理模型有利于减小不确定性。加权模型由于考虑了所有不同类型的代理模型，因此在一定程度上增加了该模型的稳健性。同时，加权模型在构造的同时充分考虑到各模型的优势，因此其精度也能得到保证。

经典的加权模型方法往往从两个指标考虑：一是考虑模型预测的方差大小，通常情况下，预测方差越小，则认为模型越准确；二是考虑模型的预测精度，即预测均值与真实值之间的偏差，加权的主要目的在于降低加权模型与真实模型之间的偏差。然而在实际应用中，预测精度高(即偏差小)的代理模型，其预测方差可能较大，或者预测方差小的代理模型，其与真实值之间的偏差比较大。本文基于以上问题，提出了基于KL(Kullback-Leibler)距离离散度的加权方法，直接对预测的分布入手，同时考虑预测的均值和方差，在兼顾预测精度的同时，降低预测模型与真实模型之间的分布差异。本文考虑两类子代理模型，一类为线性回归模型，另一类为高斯回归模型。

1 代理模型简介

1.1 线性回归模型

线性回归模型假设响应y是一类基函数(basis)的线性组合：

y=[f(x)]Tβ+

(1)

其中，x=(x1,…,xd)T为d维变量，f(x)为p维向量函数，其中每一项是关于x的基函数。通常在一类模型中基函数是给定的，因此构造线性回归模型重点在于求解未知参数β。一般假设为零均值的随机误差，因此[f(x)]Tβ实际上表示响应y的期望值。

给定N个观测(Xi,Yi),i=1,…,N，即试验设计(X,Y)，根据式(1)可以得到：

Y=Fβ+

(2)

其中，F∈RN×p为设计矩阵，=(1,…,N)T为观测误差。由于～N(0,σ2I)，可得参数β的最优线性无偏估计(Best Linear Unbiased Estimate, BLUE)为：

(3)

(4)

(5)

1.2 高斯回归模型

高斯回归模型是一类典型的非线性模型。与线性回归模型指定基函数不同，高斯回归模型建立在响应y服从某一个确定的高斯过程基础之上，即：y～GP(0,k(x,x)+σ2)，其中k(x,x)为核函数。具体来说，给定试验设计(X,Y)，则有如下似然函数：

Y|X～N(0,k(X,X)+σ2I)

(6)

记K=k(X,X)∈RN×N，由高斯过程假设以及式(6)，可得预测均值和方差分别为：

(7)

(8)

其中，K*=k(X,x)∈RN×1,K**=k(x,x)∈R。实际上，高斯过程的预测能力由核函数所决定。一般来说，针对似然函数式(6)进行优化可以得到关于核函数参数的相关估计。

2 加权代理模型

不同的代理模型其性能也有所不同，因此在加权代理模型中的权重也会随之改变。加权代理模型的一般表达式为：

(9)

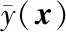
2.1 基于预测误差的权函数构造

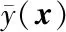
(10)

由此可求解权函数如下：

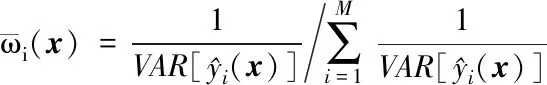
(11)

2.2 基于交叉验证均方误差和均方根误差的权函数构造

Goel[9]等选择泛化交叉验证均方误差(Generalized Mean Square cross validation Error, GMSE)作为衡量各子代理模型精度的重要参数，构造权函数如下：

(12)

其中，α<1、β<0为引入的尺度变换参数，Gi为第i个子代理模型的GMSE，即：

(13)

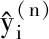
(14)

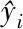
GMSE反映了代理模型在所对应试验设计点上的平均误差，GMSE越小，说明模型在该试验设计上越稳定，即模型与试验设计相适应；而RMSE反映了代理模型在测试集上的预测与真实值的误差，与GMSE相比，其在一定程度上更关注模型在全局上的预测性能，RMSE越小，其预测精度越高。同时注意到，与式(11)不同，基于GMSE(RMSE)的权函数在模型定义域上是常值，因此权函数代表各子模型整体预测性能的比重。

此外，由于GMSE对每个子模型都需要计算N次，因此会增加较大的计算量。一般情况下，可以进行并行处理或者进行k(≤10)折交叉验证。然而，针对线性回归模型，GMSE的计算可以直接进行简化，参见文献[7]第12章。对于RMSE来说，则需要增加Nv个观测，对于复杂系统来说，这会成为主要制约因素。

2.3 基于优化加权模型误差的权函数构造

Acar[10]等在前述误差的基础上，提出了基于优化误差的权函数构造方法，即求解如下最优化问题：

2012年党的十八大以来，以习近平同志为核心的党中央坚定不移地坚持高举改革开放旗帜、推进全面深化改革、扩大对外开放的战略决策部署，展现了党中央将改革开放进行到底的政治魄力和坚定决心。

(15)

其中，Err[·]表示误差函数，如RMSE或GMSE。对于式(15)的求解分为两步，首先针对试验设计构造各子代理模型，其次将各子代理模型代入式(15)求解该约束优化问题。与基于PE(RMSE, GMSE) 的方法相比，其计算量主要增加在求解最优化问题式(15)，当子模型数量M较大时，很难求得全局最优解。

3 Kullback-Leibler距离离散度加权方法

以上三类经典加权模型方法基于误差函数，往往只考虑代理模型预测的某一方面，如预测方差或偏差。本文从代理模型的预测分布入手，同时考虑这两类因素，利用Kullback-Leibler距离[11]构造权函数，从而降低预测总体分布的不确定性。

与式(9)直接假设加权模型为各模型预测值的加权不同，本文假设加权模型在各点的预测概率密度函数为各子代理模型预测概率密度函数的加权，即：

(16)

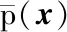
(17)

(18)

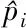
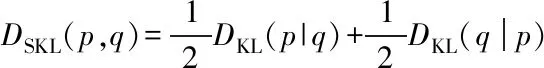
(19)

其中，DKL为通常意义下的Kullback-Leibler距离。对于本文中的两类模型，其在各点的分布服从高斯分布，同时各模型之间相互独立，因此概率密度函数p=N(μp,σp)和q=N(μq,σq)的Kullback-Leibler距离可以计算如下：

(20)

从式(20)可以看出，该距离包含预测均值和方差两种参数。基于距离的权重函数构造方法有多种，如基于反函数和减函数等特殊函数。本文拟采用高斯核函数，基于DSKL可定义权函数如下：

(21)

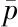
(22)

此外，尺度参数ρ可以选取为全体分布的平均离散度，即各分布之间的平均距离为：

(23)

将式(22)和式(23)代入式(21)中，并对其进行归一化可以得到最终的权函数如下：

(24)

4 算例分析

本节首先针对两个测试函数对基于Kullback-Leibler距离离散度的加权代理模型进行分析，其函数表达式如下：

f1(x)=(10cos2x+15-5x+x2)/50

(25)

(26)

其中，f1是Viana函数，f2为Rastrigin函数，且观测误差均为～N(0,0.1)。

其次，本文考虑5类子代理模型及其加权模型，其中2类属于线性回归模型，3类属于高斯回归模型。子代理模型的具体形式如表1所示。

因此，给定试验设计(X,Y)，本文比较了9类代理模型，即5类子代理模型M1～M5(如表1所示)；基于PE的加权模型M6；基于GMSE的加权模型M7；基于优化GMSE的加权模型M8；本文方法M9。同时，对于每个算例，均随机生成包含10 000个样本点的测试集(Xv,Yv)，并基于测试集比较两种指标：RMSE和经验累积分布函数(Empirical Cumulative Distribution Function,ECDF)。具体计算结果如下。

表1 5类子代理模型

4.1 Viana函数

假设x～N(0,1)，则利用拉丁超立方体抽样方法(Latin Hypercube Sampling, LHS)生成包含7个样本的试验设计(X,Y)。对每类代理模型总共进行50次独立试验，则其RMSE对比如图1所示。

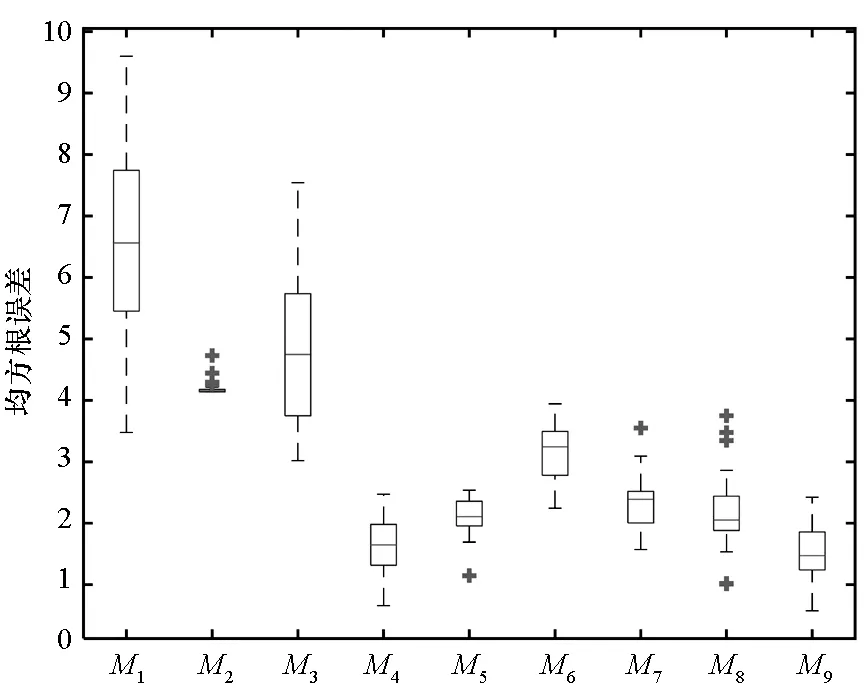
图1 9类代理模型RMSE对比Fig.1 Comparison of RMSE of 9 surrogate models

由图1可以看出，对于5类子代理模型来说，M4的逼近精度最高；对于4类加权模型来说，本文方法，即M9的逼近精度也是最高的；总体上，本文方法的精度与M4精度相近。图2利用1000个样本的测试集生成经验累积分布函数。

图2中可以看到，对比于各子模型，加权模型的ECDF都能够较好地反映真实响应的分布情形。同样地，可以看出M9与真实响应之间的差距更小，在y>5的区域上基本与真实ECDF重叠。

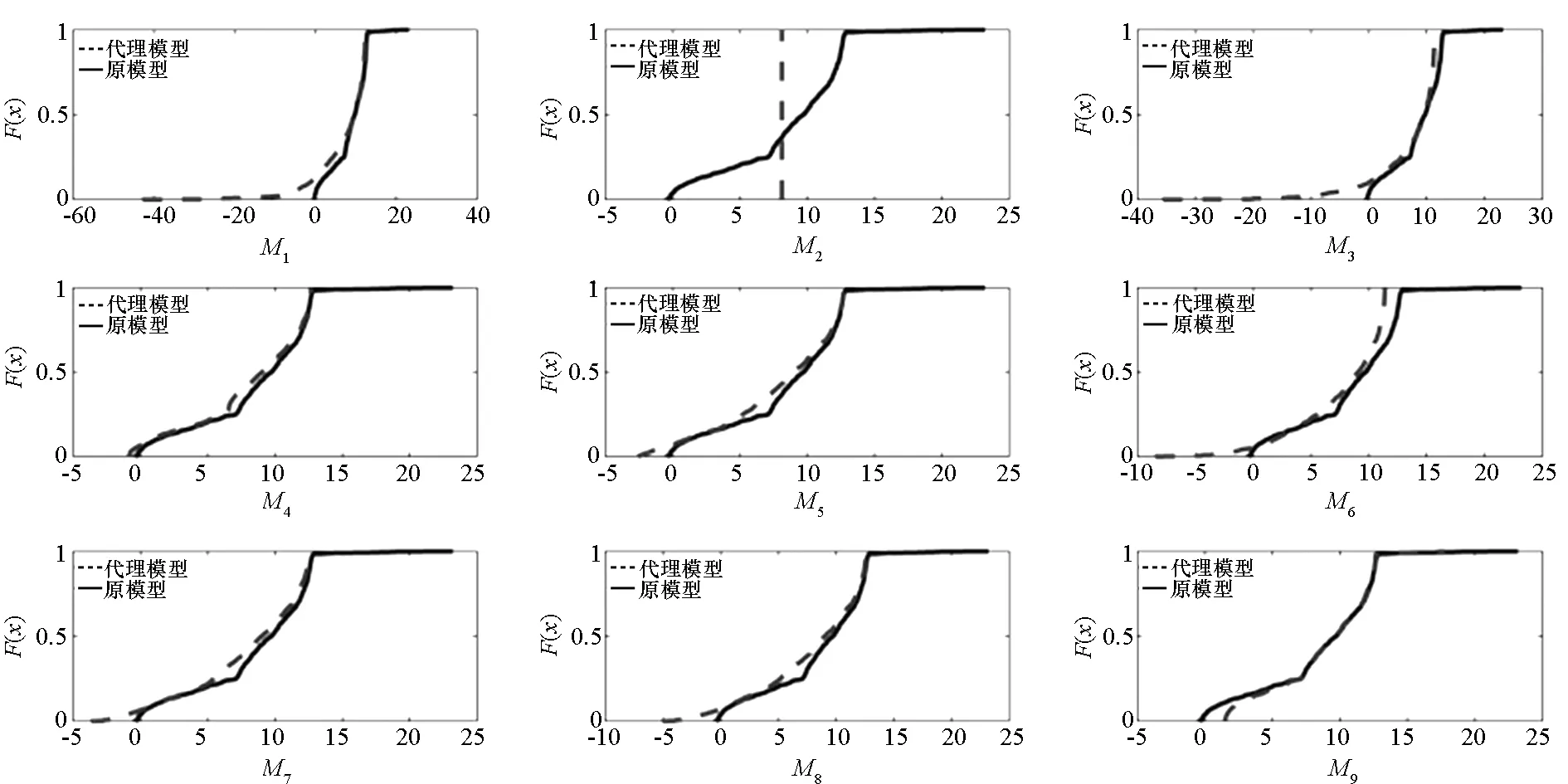
图2 9类代理模型ECDF对比Fig.2 Comparison of ECDF of 9 surrogate models

4.2 Rastrigin函数

假设xi～N(0,1),i=1,2，同样利用拉丁超立方体抽样方法(Latin Hypercube Sampling, LHS)生成包含20个样本的试验设计(X,Y)，并对每类代理模型总共进行50次独立试验，则其RMSE对比如图3所示。

由图3可以看出，对于5类子代理模型来说，除了M1以外，M2～M5逼近精度类似，其中M2,M3的整体预测性能更加稳定；对于4类加权模型来说，其预测性能与M2～M5相当，M9的逼近精度略高，在某些试验设计条件下具有最高的精度。图4与图2类似，同样利用1000个样本的测试集生成经验累积分布函数，其结果如图4所示。

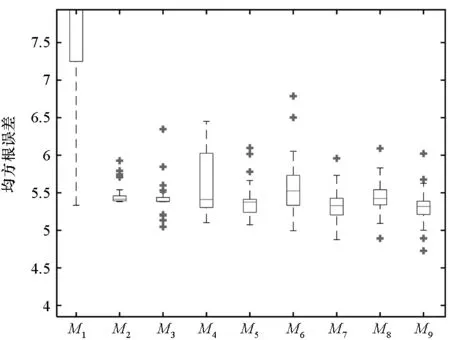
图3 9类代理模型RMSE对比Fig.3 Comparison of RMSE of 9 surrogate models

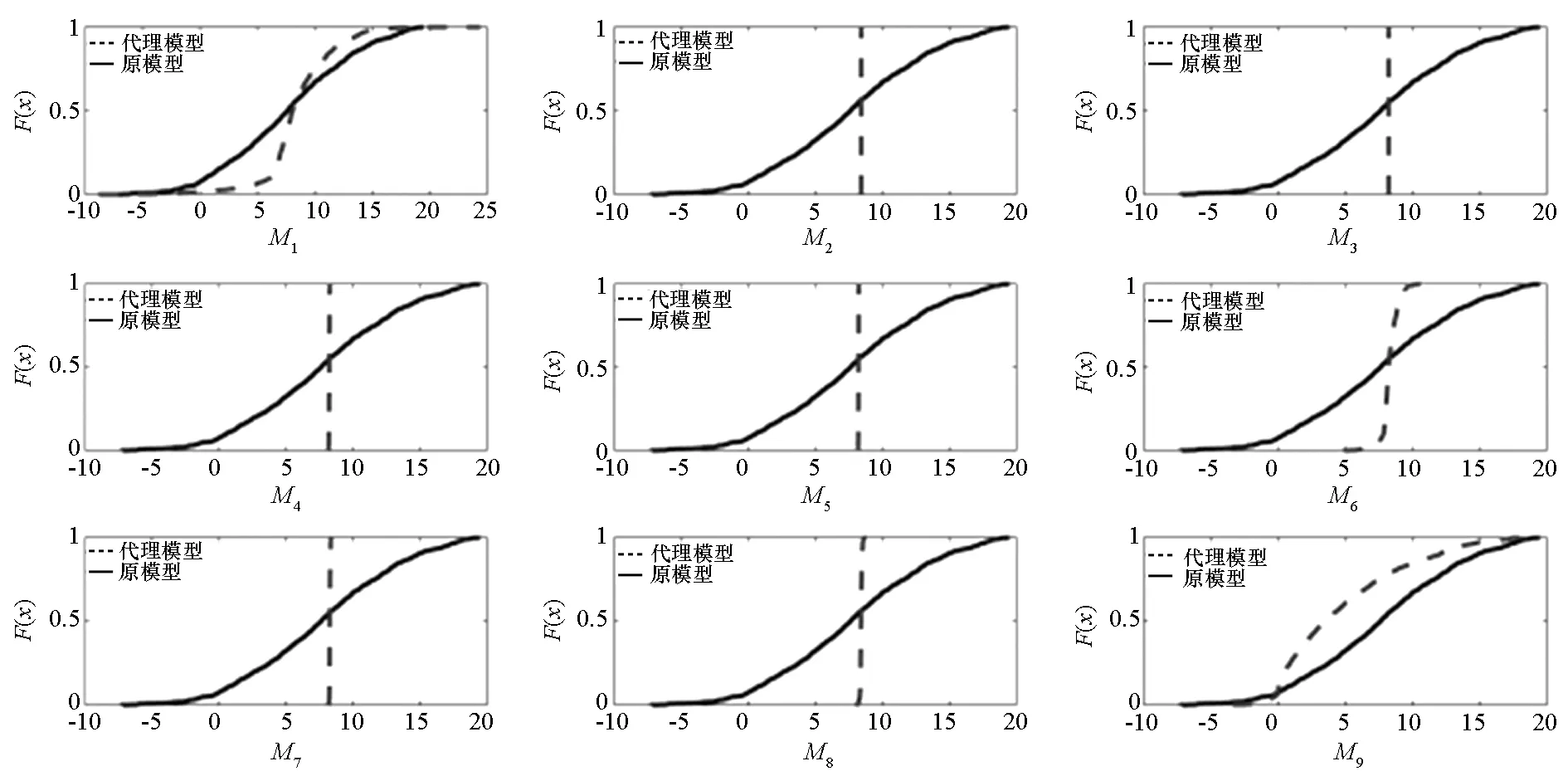
图4 9类代理模型ECDF对比Fig.4 Comparison of ECDF of 9 surrogate models

由图4可以看出，除了M1,M9以外，其他代理模型对真实响应分布逼近并不理想。同时注意到，对这些模型，其数据分布集中在y=8.4附近；作为对比，M9仍然能够较好地还原真实响应的分布。

最后对一个具体的案例进行测试，即悬臂梁(cantilever beam)问题[12]，如图5所示。

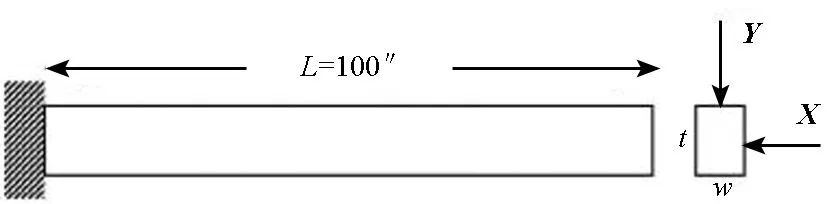
图5 悬梁臂问题Fig.5 Cantilever beam problem

其中，w和t分别代表横截面的宽度和厚度，Y表示垂直载荷，X表示水平载荷，L代表长度。对于悬臂梁问题来说，总共有两个响应，即位移D(x)和应力S(x)。具体数学表达式如下：

(27)

式中总共有三个自变量，即杨氏模量(Young′s modulus)E～N(2.9×107, 1.45×106)，垂直载荷Y～N(1000,100)，水平载荷X～N(500,100)。令w=4,t=2，同样利用LHS方法生成包含36个样本的试验设计，并对9类代理模型总共进行50次独立试验，则对于应力响应来说，其RMSE对比如图6所示。

由图6可以看出，对于5类子代理模型来说，M4、M5的预测精度较低，其RMSE远远大于200，因此未在图中展示。对于加权模型来说，M6、M7的效果同样较差，M8、M9的逼近性能相当，与最佳子模型M2的精度也在同一量级。对于ECDF来说，同样利用1000个样本的测试集生成经验累积分布函数，其结果如图7所示。

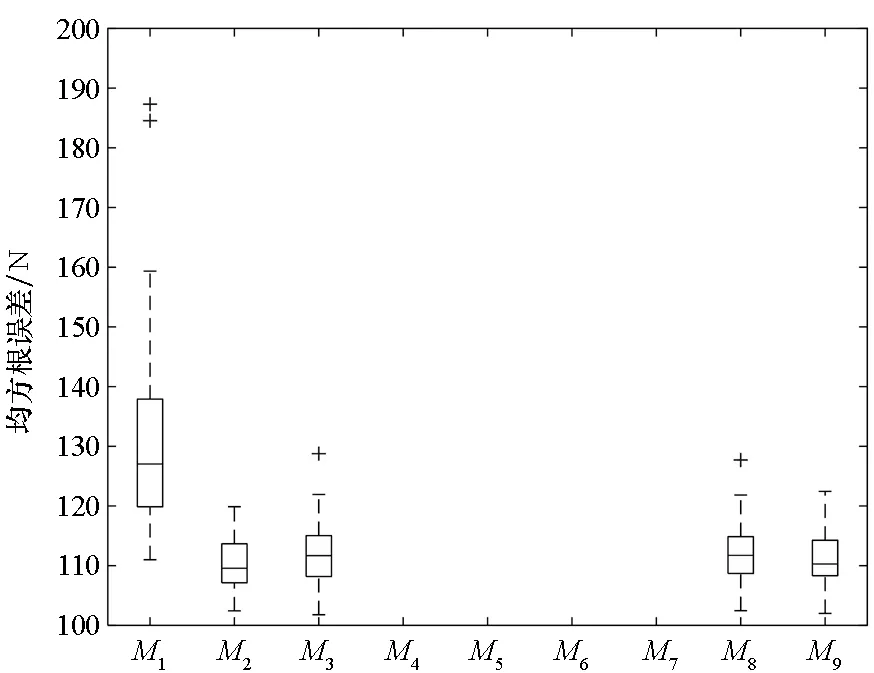
图6 应力RMSE对比Fig.6 Comparison of RMSE of stress

事实上，由图7可以看出，子模型M4、M5对本问题及试验设计的应用效果较差，而M1～M3均能够较好地估计应力的分布。对于加权模型来说，其对各子模型的“平均”作用都能使得模型更加稳健，如M6、M7，一定程度上还原了真实分布，但在性能上有着较大差异。M8、M9能够极大地利用“好”模型(M1～M3)的信息，从而其对ECDF的逼近效果也是最好的。对于位移D(x)来说，由于M3不能应用在该模型之上，因此本文仅比较其余8类代理模型。注意到此时加权模型为M1、M2、M4、M5四类模型的加权。使用与应力相同的试验设计，得到关于位移的RMSE如图8所示。

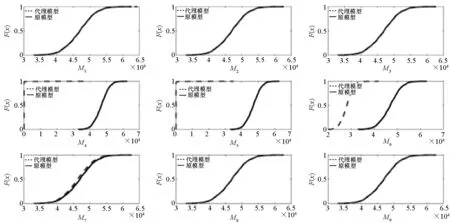
图7 应力ECDF对比Fig.7 Comparison of ECDF of stress

由图8可以看出，对于4类子代理模型来说，M4～M5其预测精度同样较低，因此也未在图中展示。对于加权模型来说，M6的效果最差，M7、M8、M9的逼近性能依次递增，一般情况下，M9的效果要比单独的代理模型都要好。利用1000个测试样本生成相关的ECDF，其对比如图9所示。

图9与图7类似，对比于各子模型，加权模型至少避免了类似M4、M5的模型选择错误，其在一定程度上能够较为稳健地逼近原模型。在所有加权类型中，本文方法与M8对ECDF的逼近是最准确的。

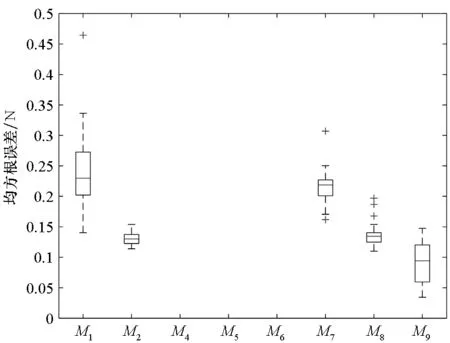
图8 位移RMSE对比图Fig.8 Comparison of RMSE of Displacement

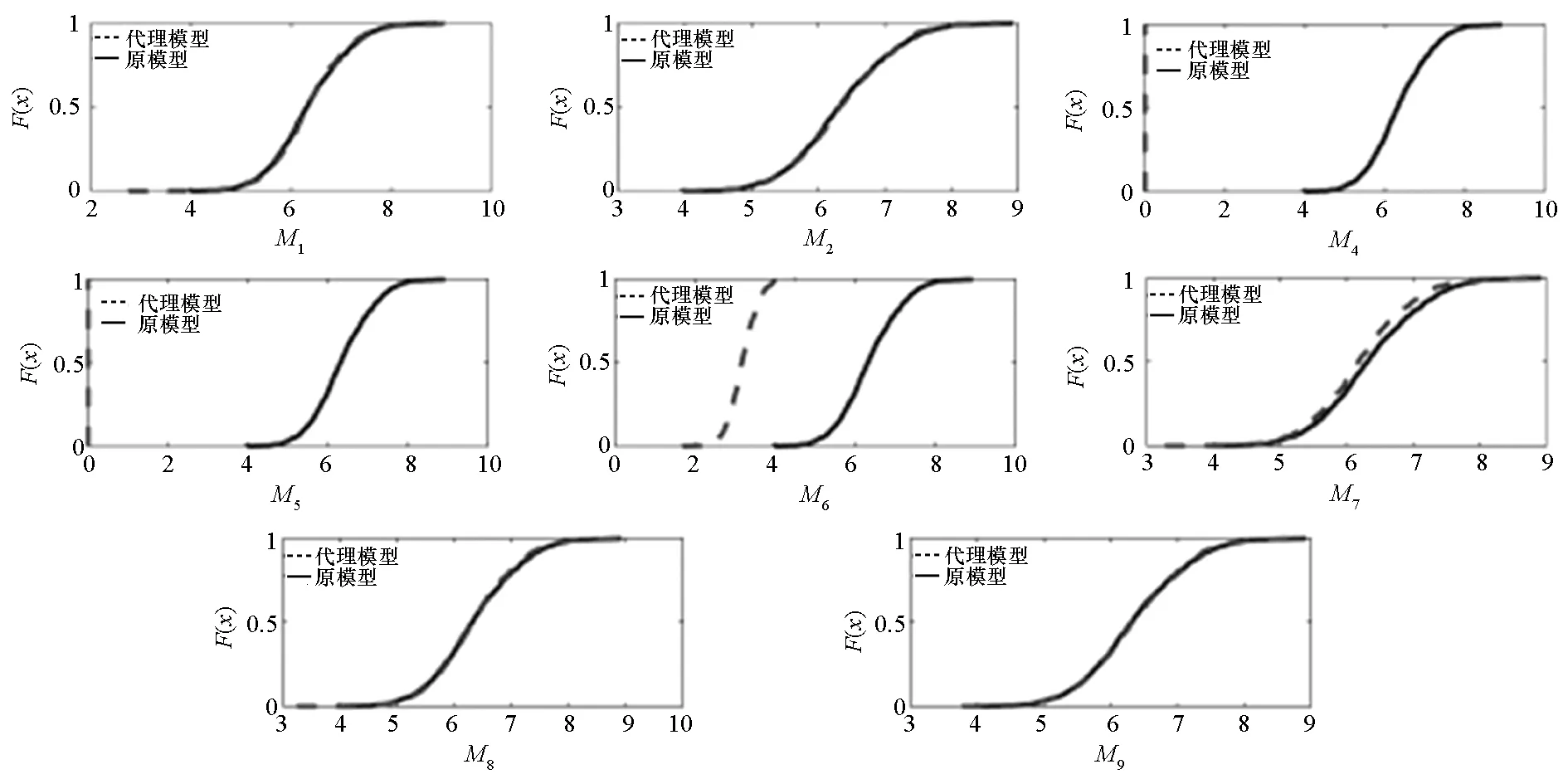
图9 位移ECDF对比Fig.9 Comparison of ECDF of displacement

5 结论

与通常加权模型选择降低加权模型精度不同，本文针对预测分布构造权函数，引入Kullback-Leibler距离刻画模型与模型之间预测分布的差异性。为了克服真实分布无法获得的问题，本文利用各模型之间的离散度来表征各模型的预测能力。算例分析表明，本文方法在兼顾模型预测精度的同时，也能够较好地还原真实响应的分布。