浮式振荡立轴叶轮的三维效应影响

张锦岚，王 凯，张万超，周亚辉

(1. 武汉第二船舶设计研究所， 湖北 武汉 430064；2. 江苏科技大学 船舶与海洋工程学院， 江苏 镇江 212003；3. 江苏科技大学 能源与动力学院， 江苏 镇江 212003)

海洋可再生能源储量丰富，总储量可达7.66亿千瓦，其开发利用逐渐受到世界各国的重视[1-3]。其中潮流能因其分布相对集中、能流密度高、有规律可循和相对稳定的属性特点[4-6]，受到更多的重视。目前潮流能开发利用，已经进入复杂海况下的定常流研究阶段。通过限定水轮机运动特性，探究复杂特殊工况下的水轮机水动力特性及能量转换是目前急需解决的任务。立轴叶轮强迫晃荡耦合运动是解决上述问题的关键，但相关研究成果还比较有限[7-9]。

目前为止，利用计算流体力学(Computational Fluid Dynamics，CFD)方法模拟叶轮的运行工况已经比较成熟。2008年，Nabavi[10]应用FLUENT软件模拟了固定偏角水轮机的性能，并采用Spalart-Ailmaras湍流模型和滑移网格技术模拟水轮机二维及三维运动，此外还分析了时间步、边界距离、叶片处网格厚度对模拟结果的影响。2014年，Danao等[11]应用FLUENT软件分析了二维和三维垂直轴风机在稳态风作用下的性能，湍流度、叶片表面节点数、边界距离及最小时间步等因素被讨论，算例采用滑移网格技术，提出时间步应取风机转过0.5°所需时间。2015年，Alaimo等[12]应用FLUENT软件模拟了二维及三维垂直轴水轮机在不同速比下的运动过程，着重分析了模拟时间步、模型网格数、叶片处网格尺寸等因素对模拟结果的影响。模型采用滑移网格技术且各算例均采用k-ε湍流模型。这些学者研究了叶轮三维和二维模拟下的叶轮水动力性能影响。对于立轴叶轮在浪流作用下发生振荡运动的三维和二维水动力性能差别还少有学者进行研究。

近几年，一些学者对浪流作用下的水平轴水轮机的水动力性能做了一些研究[13-16]，这些学者认为浪流作用下水平轴水轮机的水动力会发生波动，力和力矩的峰值会提高，但是平均值基本不变。哈尔滨工程大学张亮团队从潮流能水平轴水轮机实际运行中也发现浪流作用对水轮机的水动力性能有明显影响。

1 数值模拟

1.1 理论基础

表1为立轴水轮机振荡运动下的各参数定义。表1除去常规的叶轮参数定义外，特别定义了叶轮振荡运动下的振荡幅值、振荡频率和振荡速度。

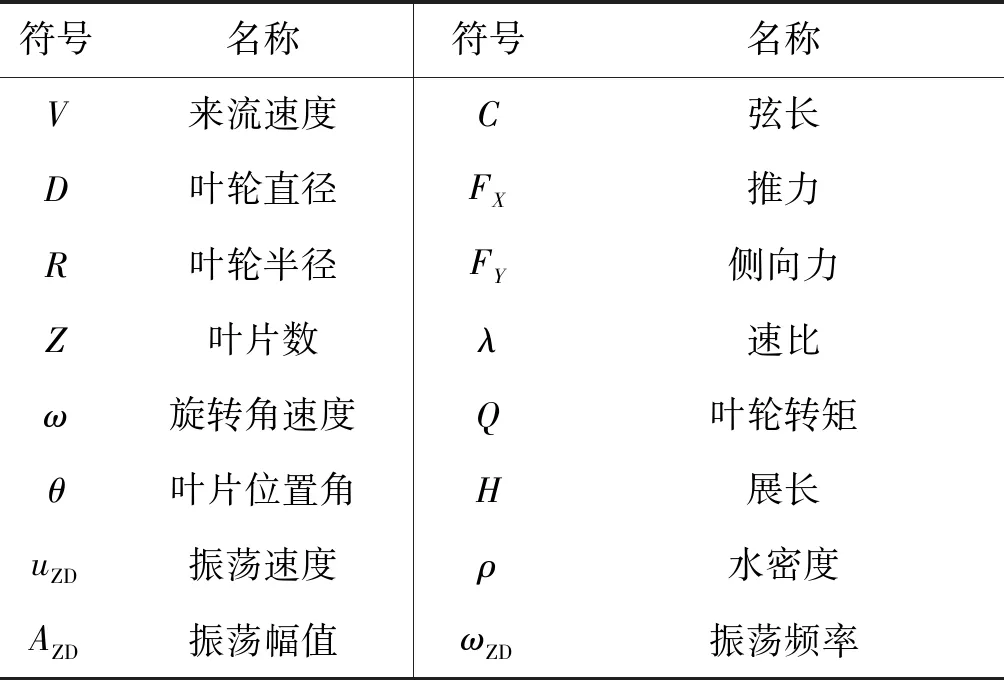
表1 立轴水轮机叶轮参数

通过表1，定义无量纲参数如下：

推力系数

CFX=FX/(0.5ρ·V2·D·H)

(1)

侧向力系数

CFY=FY/(0.5ρ·V2·D·H)

(2)

能量效率系数

Cp=Q·ω/(0.5ρ·V3·D·H)

(3)

叶尖速比

λ=R·ω/V

(4)

无因次振荡速度

(5)

无因次振荡加速度

(6)

为了简化描述，使用变量Φ来表示坐标轴方向，其中Φ为X时表示X轴方向，Φ为Y时表示Y轴方向。叶轮的受力可以分解为三类，即均匀水动力、阻尼力和附加质量力，则叶轮受力表示为

(7)

对阻尼力和附加质量力进行分解，表示为

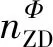
(8)

(9)

其中，ψ表示叶轮位置角和各项展开项的错位角。将式(8)和式(9)代入式(7)，则叶轮振荡运动下的受力可表示为

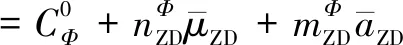
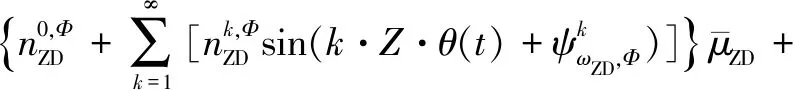
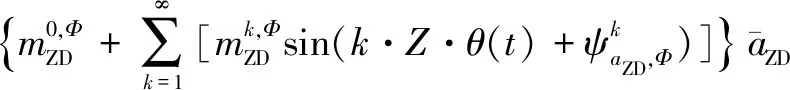
(10)

利用ANSYS-CFX软件对立轴叶轮振荡运动进行模拟仿真，并将得到的叶轮振荡运动下的推力和侧向力时历曲线利用最小二乘法拟合，就可以得到式(10)中的各项系数，总结对比二维模拟和三维模拟各参数对立轴叶轮振荡运动的影响规律。

1.2 立轴水轮机模型

选用双叶片叶轮模型，其叶片采用NACA0018对称翼型，叶轮直径为0.8 m，弦长为0.12 m，来流速度为1.0 m/s。

图1和图2分别为立轴振荡叶轮数值计算的二维和三维网格模型。本文主要计算叶轮旋转运动和振荡运动相结合工况下的二维和三维结果，其中振荡运动包括横荡运动和纵荡运动。两幅图中分别给出了二维和三维工况下的各运动形式计算域，主要包括旋转域、振荡域和随振荡运动网格发生微幅变形的变形域。

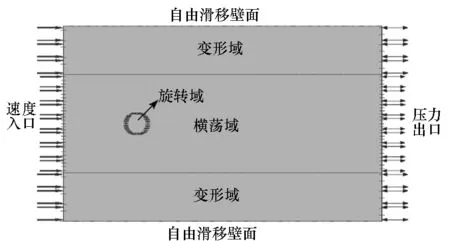
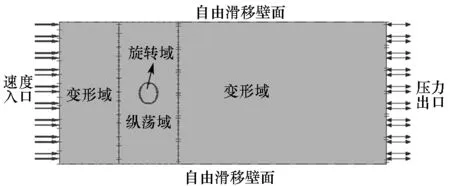
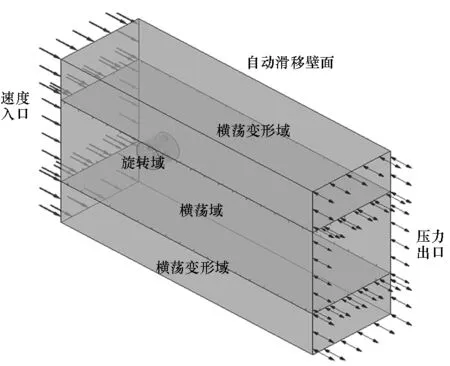
图3为叶轮振荡运动模拟设置的边界条件。边界条件的设置和常规旋转叶轮的边界条件设置类似，所不同的是本文中将旋转域以外的流场域分为振荡域和振荡变形域，其中振荡域在计算中发生横荡或者纵荡运动，运动过程中网格只存在滑移运动，网格不发生变形；振荡变形域在计算中网格发生微幅拉伸和压缩，但是对网格质量几乎没有影响。

(a) 叶片(a) Blade (b) 旋转域(b) Rotation domain

(c) 横荡域(c) Sway region (d) 横荡变形域(d) Sway deformation region

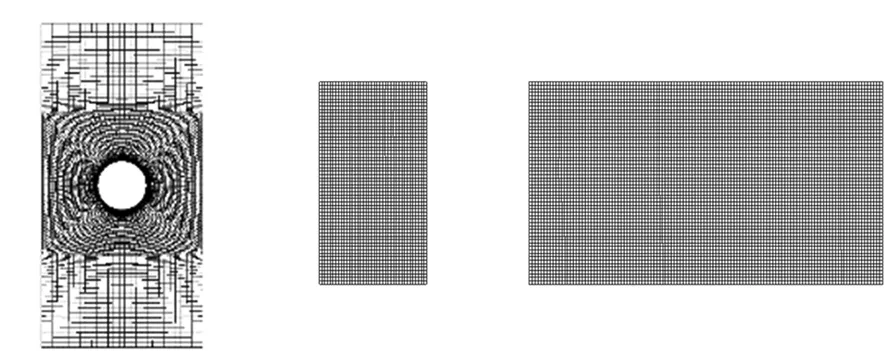
(e) 纵荡域(e) Surge region (f) 纵荡变形域(f) Surge deformation region 图1 二维网格模型Fig.1 2D grid model

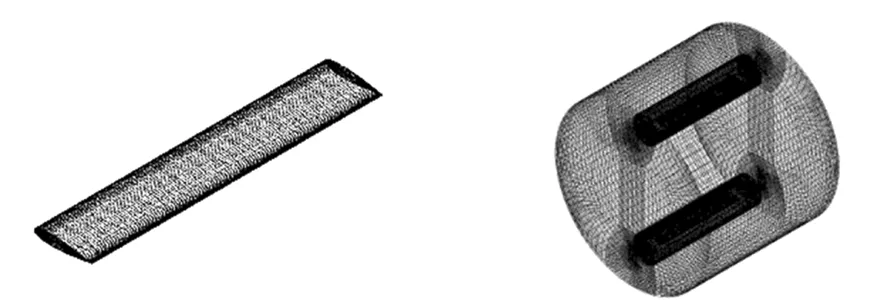
(a) 叶片(a) Blade (b) 旋转域(b) Rotation domain

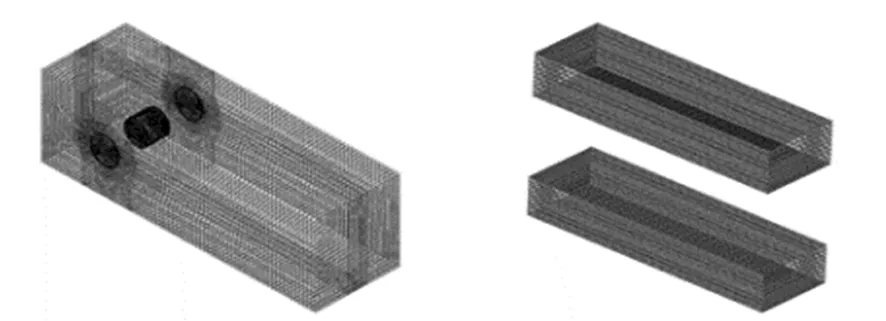
(c) 横荡域(c) Sway region (d) 横荡变形域(d) Sway deformation region

(e) 纵荡域(e) Surge region (f) 纵荡变形域(f) Surge deformation region图2 三维网格模型Fig.2 3D grid model

(a) 二维横荡(a) Two-dimensional sway motion

(b) 二维纵荡(b) Two-dimensional surge motion

(c) 三维横荡(c) Three-dimensional sway motion

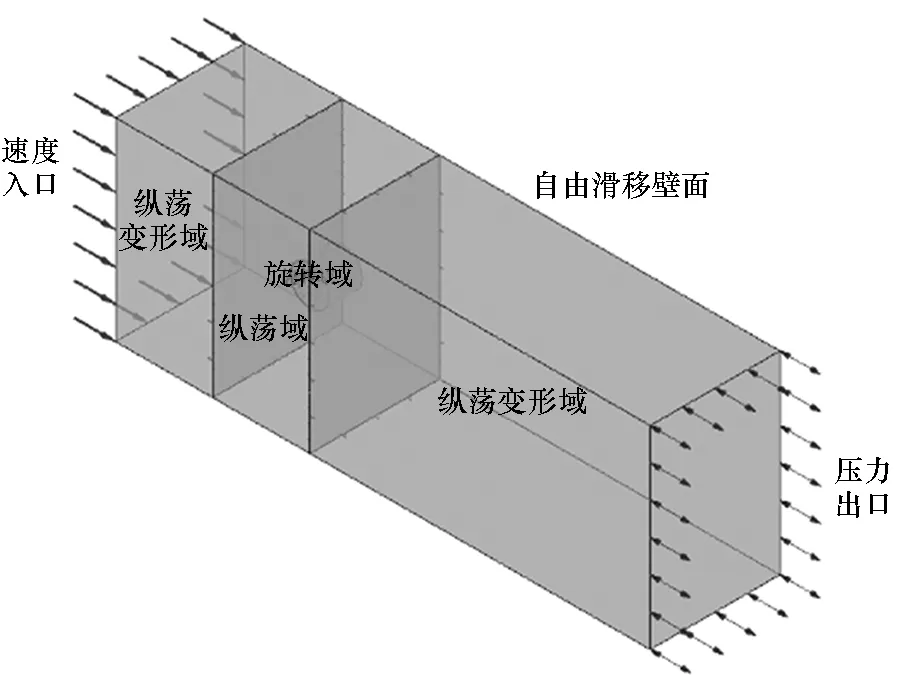
(d) 三维纵荡(d) Three-dimensional surge motion图3 边界条件Fig.3 Boundary conditions

2 结果分析

2.1 CFD方法的可行性证明

在计算模拟前，首先验证立轴叶轮仿真计算的有效性，分别从二维模拟和三维模拟方面对计算值和试验值进行对比分析。

二维计算验证：采用本文的计算方法对美国Strikland教授做的关于立轴叶轮的二维试验[17]进行模拟，并将计算得到的单个叶片切向力、法向力与试验结果对比。图4为试验值和本文计算结果的对比，从两幅图中可以看出，计算结果和试验值相近。教授也对该叶轮进行了数值模拟计算，本文结果和其计算结果类似，在90°～270°的上游盘面，计算值和试验值误差较小，而270°～450°的下游盘面误差较大。Strikland教授分析可能是：一方面试验时叶片安装有问题，造成下游盘面试验值存在凸起现象；另一方面下游盘面水流受到上游盘面影响，水流复杂，导致试验值和计算值存在一定差异。

为了验证本文计算方法三维模拟的有效性，对比了哈尔滨工程大学“HEU”型两叶片立轴水轮机的水动力性能，结果如图5所示。图5(a)和图5(b)分别为叶轮效率和推力的试验值和三维计算值对比。不论是效率还是推力，三维仿真计算结果都略大于试验值，这是因为仿真计算中未考虑叶轮运行过程中机械摩擦、壁效应的影响，这些影响都会造成叶轮效率和推力的降低。综合来看，立轴叶轮三维模拟计算精度较高，能够模拟立轴叶轮真实运行情况。

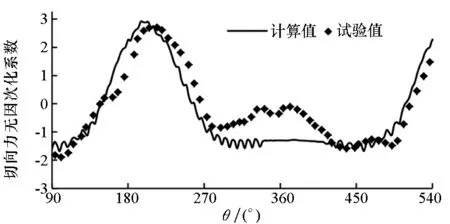
(a) 切向力(a) Tangential force

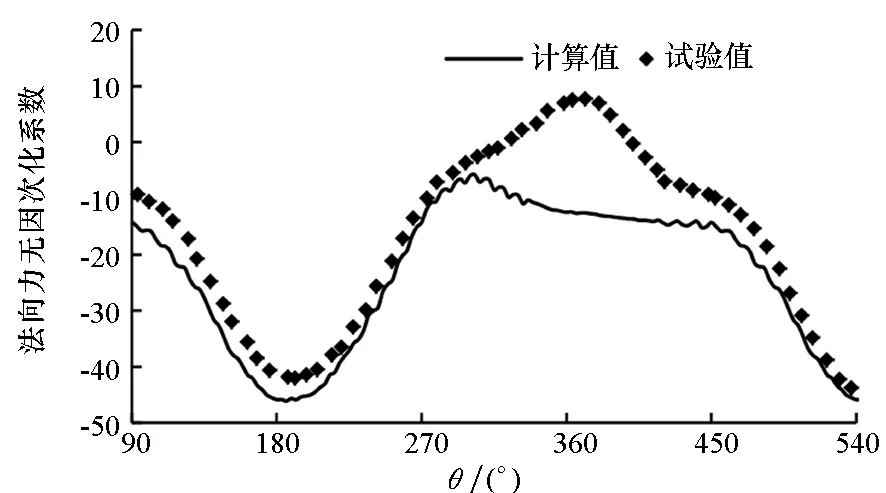
(b) 法向力(b) Normal force图4 二维计算对比图Fig.4 Comparisons between calculated and experimental values

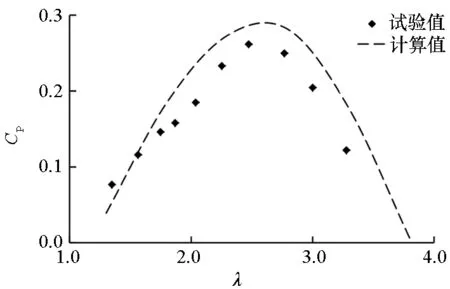
(a) 效率对比(a) Comparison of efficiency

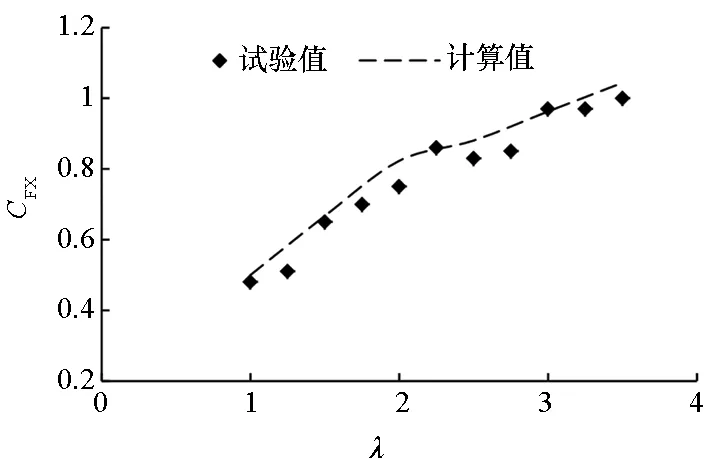
(b) 推力系数对比(b) Comparison of thrust coefficient图5 三维计算对比Fig.5 Results comparison between the experimental and 3D numerical simulation

2.2 立轴叶轮振荡运动效率

当展弦比较小时，叶轮振荡运动下二维计算和三维计算结果相差较大。为了寻找不同展弦比下二维结果和三维结果的变化规律，首先计算了不同展弦比的立轴叶轮振荡运动，并将效率作为对比对象和二维结果进行比较。如图6所示，两图为横荡运动和纵荡运动下不同展弦比三维叶轮效率和二维效率对比的结果。随着展弦比增大，三维计算结果逐渐增大，当展弦比达到10左右时，三维计算结果和二维计算结果相近。叶轮三维计算结果和二维计算结果存在差异的最主要原因是三维计算中存在三维效应，叶片展长两侧存在机翼绕流，叶梢处高压区流体会流向低压区，造成叶梢处尾涡，带走一部分能量，因此叶轮三维效率计算结果小于二维计算结果。

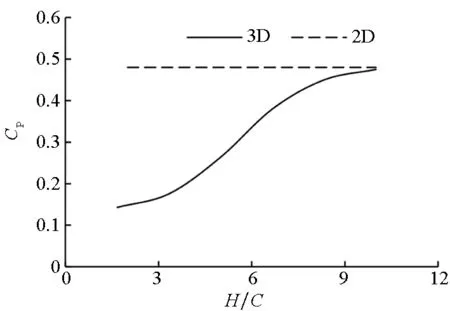
(a) 横荡运动(a) Sway motion

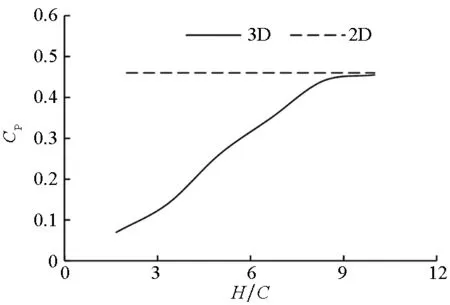
(b) 纵荡运动(b) Surge motion图6 不同展弦比的水轮机效率曲线Fig.6 Comparison of power output curves of vertical axis turbine with different span-chord ratios

2.3 立轴叶轮振荡运动推力和侧向力

图7所示为叶轮横荡和纵荡运动下的不同展弦比的推力系数和侧向力系数的对比。其中图7(a)和图7(c)为推力系数对比，图7(b)和图7(d)为侧向力系数对比。四幅图中分别对比了展长为0.2 m、0.6 m和1.0 m的三维计算结果和二维计算结果。从四幅图中可以看出，随着展长增大，相对应的推力和侧向力系数逐渐接近二维计算结果。推力和侧向力的波峰和波谷都随着展长增大而增大。这是因为展长越长，叶轮的三维效应影响越小，叶梢处尾涡带走的能量越少，计算结果越接近二维计算值。

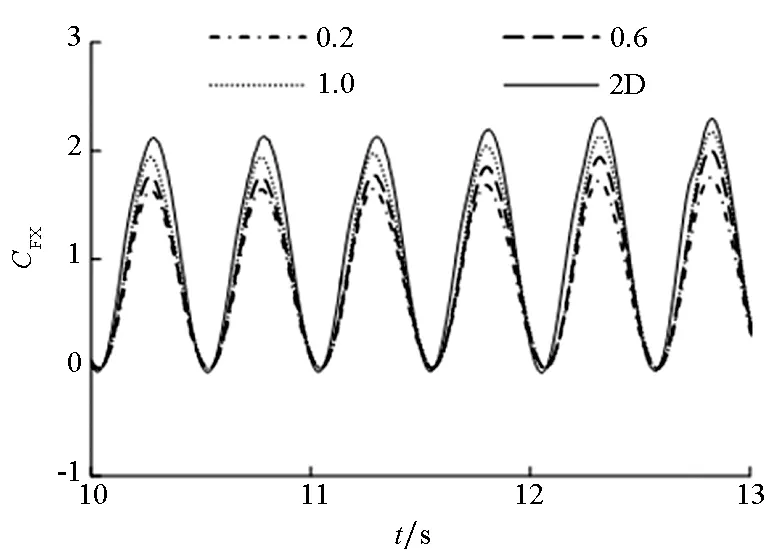
(a) 横荡推力(a) Thrust of sway

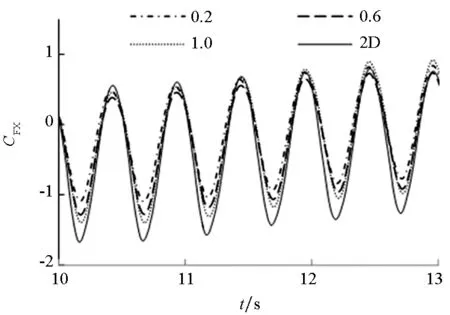
(b) 横荡侧向力(b) Lateral force of sway

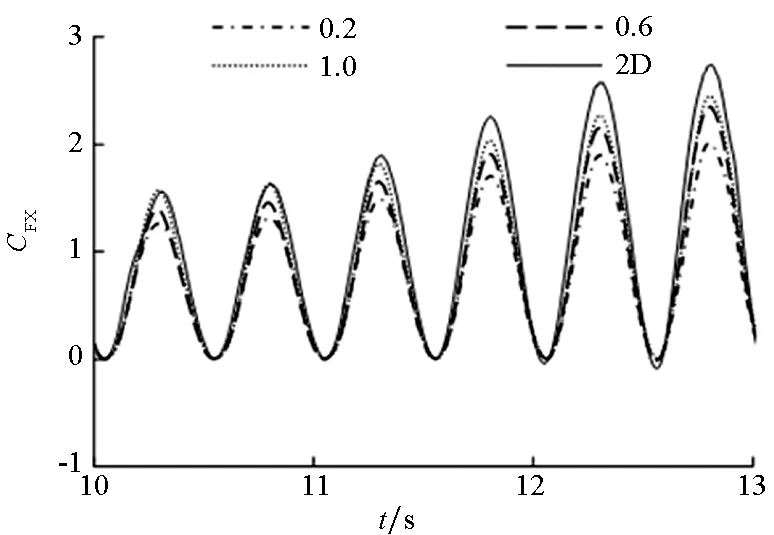
(c) 纵荡推力(c) Thrust of surge

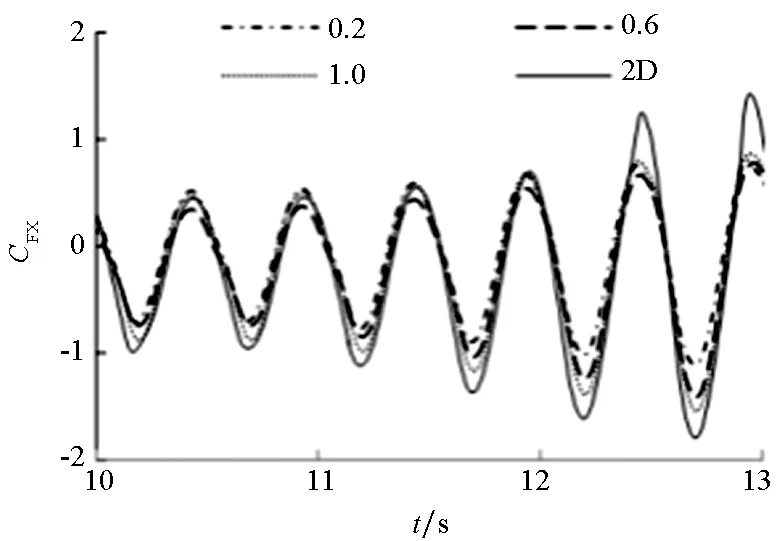
(d) 纵荡侧向力(d) Lateral force of surge图7 不同展长的叶轮振荡状态下的推力和侧向力系数对比Fig.7 Comparison of thrust and lateral force coefficients under swaying motion and surging motion of different elongation

图8为三个不同展长的叶轮流场图，从三幅图中可以看出上游叶片叶梢两端产生流体分离，带走了一部分能量。图8(a)所示展长0.2 m的叶轮流体分离几乎布满整个叶片，明显大于图8(b)和图8(c)。结合图9所示的不同展长的叶轮涡量场，在同一涡量指标下，展长0.2 m的叶轮两端涡量强度明显大于0.4 m和0.6 m展长的涡量强度，其带走的能量也越多，因此导致叶轮水动力性能降低。

从图8和图9可以看出，展弦比越大，叶轮由于三维效应在叶片两端产生的尾涡越小，带走的能量也越小，因此叶轮效率、推力等水动力系数越高。结合2.2节，当叶轮的展弦比达到10左右时，叶轮尾涡带走的能量可以忽略不计，水动力性能也与二维叶轮的水动力性能相近。

(a) H=0.2 m (b) H=0.4 m (c) H=0.6 m图8 不同展长的叶轮流场流线图Fig.8 Streamlines of the flow field under different elongations

(a) H=0.2 m (b) H=0.4 m (c) H=0.6 m图9 不同展长的叶轮涡量场Fig.9 Vorticity fields under different elongations

3 水动力系数

根据式(10)将三维模拟计算得到的不同展长的立轴叶轮推力和侧向力系数进行拟合分析，得到各受力系数的均匀水动力、阻尼力和附加质量力系数。如表2～5所示，对比了0.2 m、0.4 m、0.6 m、0.8 m四个展长和2D模拟横荡与纵荡运动下的各项系数。

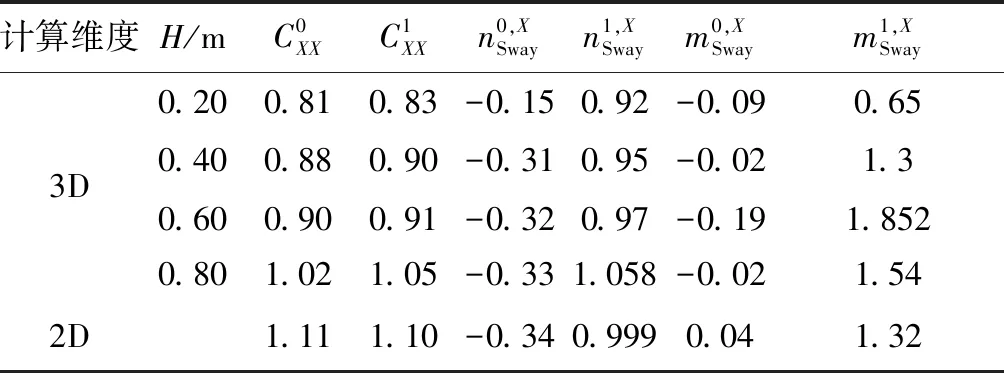
表2 横荡运动CFX展开系数

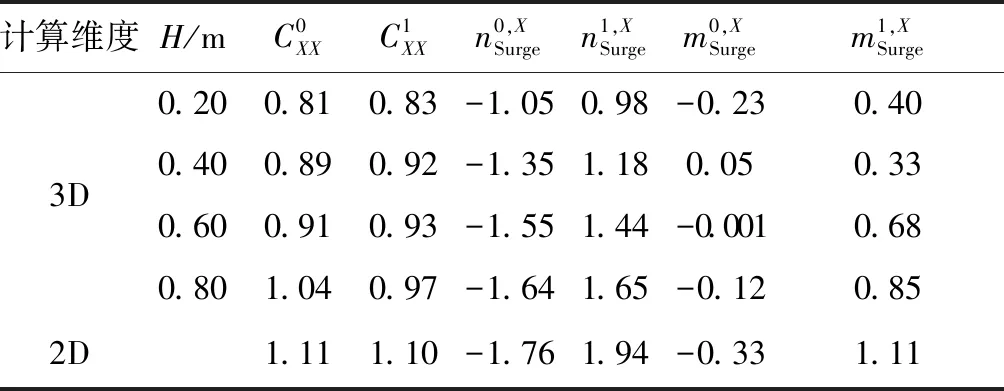
表3 纵荡运动CFX展开系数

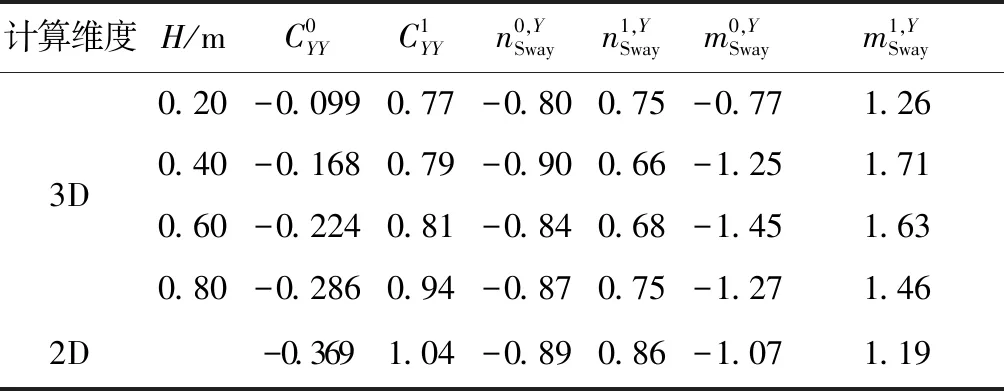
表4 横荡运动CFY展开系数

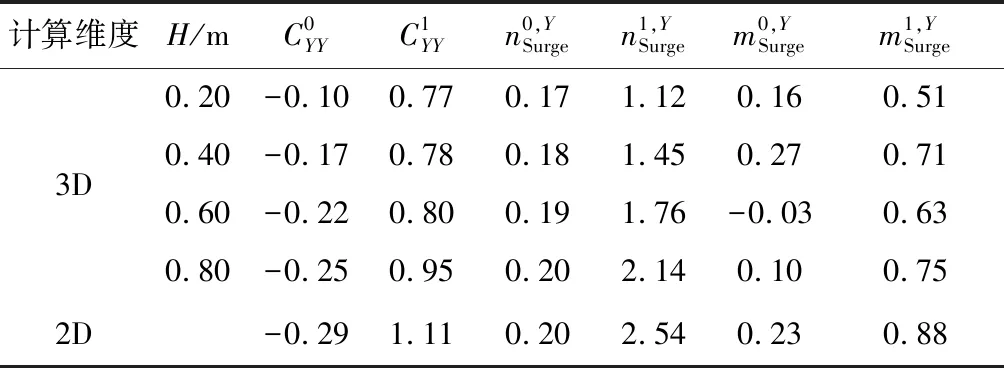
表5 纵荡运动CFY展开系数

表4和表5为振荡运动下侧向力的展开系数，规律和表2、表3类似。随着展长增大，振荡叶轮的侧向力展开项中附加质量力所占比例较小，且另外两项系数绝对值随着展长增大而增大，逐渐接近二维结果。

4 结论

利用流体计算软件ANSYS-CFX计算了不同展弦比的叶轮三维振荡运动，包括横荡和纵荡运动，并将计算结果和二维模拟结果做了对比，结论如下：

1)立轴叶轮三维模拟结果中水动力系数和二维结果存在一定差异，当展弦比接近10时，三维结果和二维结果相差不大。

2)随着展弦比增大，三维振荡叶轮的输出效率、推力和侧向力系数逐渐增大。

3)三维振荡叶轮的水动力性能计算结果低于二维计算结果，最主要原因是三维叶片两端流体从高压区流向低压区，造成能量损失。

4)三维振荡叶轮的推力和侧向力各项中，附加质量力和均匀水动力、阻尼力相比为小量。