复杂网络影响力极大化快速评估算法
2019-06-19王潇杰赵城利易东云
王潇杰,赵城利,张 雪,易东云,2
(1. 国防科技大学 文理学院, 湖南 长沙 410073;2. 国防科技大学 高性能计算国家重点实验室, 湖南 长沙 410073)
研究网络科学的主要目的之一是解决复杂网络上的动力学问题,对于网络上动力学特性的研究一直是网络科学研究领域的重点与难点。特别地,对于网络传播动力学的研究更是具有极为重要的现实意义。传播现象在现实生活中无处不在,例如谣言在社交媒体上的传播[1],传染病在人群中的传播[2],以及电力网络的级联故障[3]等。对于传播动力学的研究可以揭示复杂网络中的传播机理以及动力学行为,从而提供对这些行为的切实可行的控制方法,创造巨大的经济价值和社会价值。在现实生活中,人们经常面临的一个实际问题就是高效地寻找少部分具有重要影响力的初始传播者。例如,对于一个新产品的市场营销而言,选取少量的种子用户作为产品推广人,利用口碑营销的方式迅速打开市场、提高产品知名度,是十分重要的。在网络科学的领域中,这种通过选取少量节点作为初始节点,以极大化这些节点在整个网络中的传播影响力的问题,称为影响力极大化问题[4]。
关于影响力极大化问题的研究可以追溯到Domingos等的工作[5],他们第一次研究了如何将影响力极大化问题表述为一个算法问题,并提出了一种基于概率的算法用于近似求解。此后,Kempe等[6]利用社会网络分析的方法系统地研究了这个问题,他们发现,网络中的影响力极大化问题的实质是NP-hard的组合优化问题,其精确求解非常困难。进一步地,他们给出了一个基于贪婪思想的算法以近似求解影响力极大化问题,并证明了该算法的精确度下界。然而,由于该算法十分耗时,往往只能应用在不大的网络上进行求解。基于类似的贪婪思想,Leskovec等[7]通过对影响力极大化问题的子模块性质进行研究,提出了高效贪婪选择(Cost-Effective Lazy Forward selection, CELF)算法,提高了Kempe算法的效率。在CELF算法的基础上,Goyal等[8]对于算法步骤进一步优化,提出CELF++算法,极大提高了CELF算法的效率。
虽然基于贪婪思想的算法大多可以取得较为满意的结果,较高的算法复杂度往往成了限制它们应用的一个关键因素。因此,越来越多的学者开始尝试提出启发式算法来近似求解影响力极大化问题。Narayanam等[9]另辟蹊径,通过引入博弈论中的Shapely值的概念,提出了基于Shapely值的重要节点选择(ShaPley value based Influential Nodes,SPIN)算法。Zhao等[10]受到地图着色问题的启发,提出了一种基于着色的算法。Zhang等[11]提出了基于迭代的投票排名算法,可以有效地识别一组影响力较大的离散节点。通过分析节点的相对关系,Chen等[12]提出了折扣度算法,很好地平衡了算法的计算效率和精确度,取得了不弱于贪婪算法的结果,已成为现在影响力极大化问题的标准算法之一。Lü等[13]分析了度中心、H指数以及核数的关系,验证了H指数在描述节点重要性的良好表现。近年来,Morone等[14]研究了网络中的级联失效问题,提出了基于最优渗流理论的集群影响算法,可以有效识别级联失效问题中的重要节点。
通常而言,大多数启发式算法往往通过某种重要性指标来间接反映节点的影响力。本文结合网络上具体的传播动力学分析,提出快速评估算法,通过期望计算的方式直接估计节点的传播影响力,并进一步运用序列采样的策略进行种子集的快速选择,在保证算法效率的基础上极大提高了算法的精度。
1 影响力极大化问题分析
沿用图论中的相关记号,网络可以用图G(V,E)来表示[15],其中节点V代表网络中的个体,边E代表个体之间的联系。例如对一个在线社交网络而言,用户就是网络中的节点,用户之间的好友关系自然而然地构成了网络中的边。
在一个网络中,影响力极大化问题可以描述为:如何寻找网络中的L个节点S⊂V作为种子节点(即信息的初始传播者),将信息传播到网络中尽可能大的范围。
对于影响力极大化问题,一个直观的想法是,如果可以对节点在网络中的重要性进行排序,依次选取排名靠前的节点,它们在整个网络中的集群影响力自然会大。例如,可以利用网络中的各种中心性指标[15]对节点进行排序,依次选取排序中靠前的部分节点作为种子节点来极大化它们在整个网络中的影响力。事实上,这种选取方式存在一个严重的问题——由于节点在网络中的影响力存在着相互重叠的区域,节点间的相对位置必然会对它们的集群影响力造成重要的影响,这也是影响力极大化问题的难点所在。
通常而言,针对网络上不同的信息传播方式,最优的初始传播者会有所不同,很难找到一种统一的算法适用于所有传播动力学下的影响力极大化问题。在下面的分析中,将主要讨论一种简单的信息传递模型。假定网络中所有的节点都可能具有两种状态,即接收态与未接收态。处于未接收态的节点,代表网络中还没有接收到信息的普通个体;而处于接收态的节点,则代表那些接收到信息的个体,它们会以概率p向周围邻居广播消息,进而将消息扩散到整个网络中。
2 影响力极大化快速评估模型
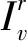
当r=1时,对于所有的普通节点v∈V-S,它们会受到周围种子节点的影响而转化为接收态,其概率为:
(1)
式中:p为信息传递概率;Γv为节点v的邻居,tv=|Γv∩S|为节点v的种子节点邻居数量。
当r≥2时,信息传递由所有处于接收态的节点进行,这包含两部分节点:初始时刻的种子节点,以及在之前时刻转化为接收态的普通节点。因此,对于一个非种子节点v∈V-S,它在第r轮信息传递时处于接收态的概率为:
(2)
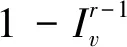
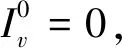
(3)
综合上述分析,当种子节点集为S时,在第r轮信息传递中,网络中的某节点v处于信息接收态的概率为:
(4)
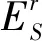
(5)
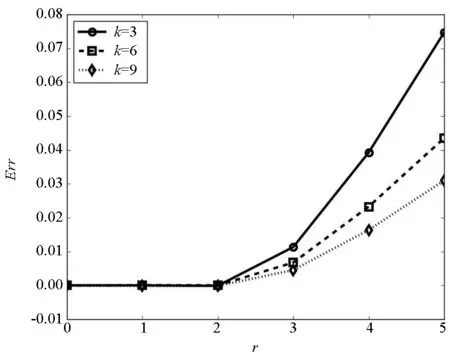
(a) 幂指数为2.1时近似误差图(a) Errors of the approximations when γ=2.1
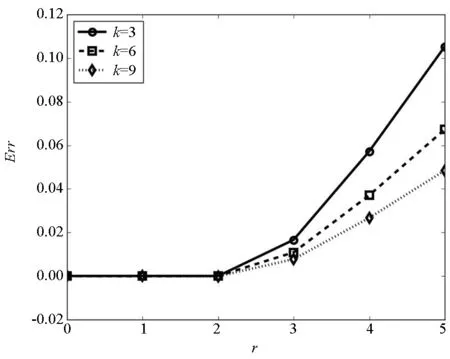
(b) 幂指数为3.0时的近似误差(b) Errors of the approximations when γ=3.0图1 不同幂指数时的近似误差图Fig.1 Errors of the approximations with different γ
图1显示了不同幂指数时的近似估计与真实传播范围的误差。仿真网络的规模均为10 000个节点,平均度分别为3,6,9,初始传播者为随机选取的100个节点,传播概率为p=1.1pc,其中pc为疾病阈值。图1中的线代表真实传播范围,符号代表近似估计结果。从图1中可以看出,在传播的早期,近似估计结果与真实传播范围符合得很好,随着传播过程的进行,二者的差距逐渐增大,这种趋势在平均度较小的稀疏网络中表现得更为明显。由于影响力极大化问题通常关注的是网络上的早期传播行为,本估计基本可以满足精度方面的需求。
通过式(5),可以快速计算种子节点集S在整个网络中的集群影响力,特别地,可以用来评估将一个新的节点v加入种子节点集所带来的集群影响力增量。
(6)
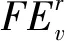
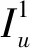
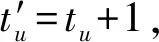
而对于与节点v不相邻的节点u∉Γv-S,它们转化为接收态的概率不会发生变化。
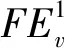
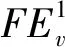
=1+(dv-2tv)p
(7)
当r=2时,由式(3)可知,节点u∉S转化为接收态的概率为:
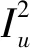
通过近似和简化,可以得到
由上述可知,该近似过程仅需用到节点u自身的种子节点邻居数量以及邻居节点的种子节点邻居数量。
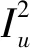
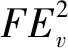
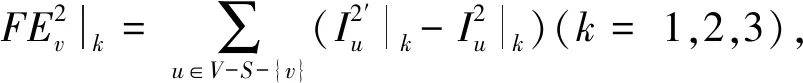
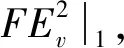
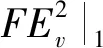
=2(dv-tv)p
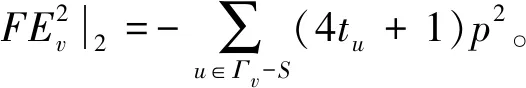
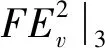
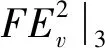
(8)
由此提出一种启发式算法,用以近似求解网络中的影响力极大化问题。算法采用序列采样的方式,按照种子集扩展的方式,每次从所有候选节点中选取一个对种子节点集影响力增量最大的节点加入种子集,直到足够数量的种子节点被选出,构成影响力极大化问题中的初始传播者。假定信息传递概率为p,传递轮数为r,种子节点数目为L,如算法1所示。

算法1 影响力极大化快速评估算法
在传统的基于贪婪思想的影响力极大化算法中,需要通过大量的随机仿真来计算种子节点的集群影响力,这导致算法复杂度激增,即便只是在一个中等规模的网络中寻找极少数量的种子节点也需要花费非常长的时间,难以用来求解现代大规模商业和社交网络上的影响力极大化问题。与传统算法不同,本算法运用近似估计的方式,可以直接计算候选节点的集群影响力增量,加快了影响力极大化问题的求解速度。通常而言,传播轮数越多,快速评估算法的计算复杂度就越高,为了兼顾算法的效率和精度,在后面的实验中,固定参数r=2。
3 算例分析
3.1 传播模型
当选出种子节点之后,需要通过传播模型来度量这些节点在网络上的传播能力,这里考虑一个更为符合现实中消息传播模式的易感-感染-恢复(Susceptible-Infected-Recovered, SIR)模型[16]。该模型最早被用来研究传染病在人群中的传播行为,在该模型中,每个节点可以处于三个状态:易感态S、感染态I以及恢复态R。易感节点指的是那些尚未被感染的个体,可能以概率p被周围处于感染态的个体感染。对于感染节点,它们代表那些感染了疾病的个体,在下一个时间片上,以概率q康复,即转为恢复节点。
在经典的SIR模型中,每个感染节点可以同时尝试感染所有的易感邻居。然而,在现实生活中,一个更加常见的现象是一个处于感染状态的节点仅仅可以尝试感染一个处于易感状态的邻居(例如握手行为)。因此,这里使用有限感染的SIR模型[17]进行仿真。在初始时刻,种子节点被标记为感染状态,其他节点均为易感状态,此后,在每一个时刻,每个感染者以概率p随机选取一个邻居节点进行感染,然后以概率q恢复。定义有效传播率为感染概率与恢复概率的比值。当网络中没有感染者时,整个传播过程结束,最终感染的节点越多,说明种子节点的影响力越大。
3.2 数据描述
为了验证快速评估算法在影响力极大化问题中的表现,选取6个不同类型的真实网络进行验证,分别为:邮件网络[18]——反映了Enron公司内部近50万封邮件的收发关系;合作网络[19]——隶属于计算机科学的科学家合作网络;购物网络[19]——一个共同购买网络,来自购物网站Amazon上的共同购买信息;分享网络[20]——文件分享网站Gnutella上的p2p网络;信任网络[21]——一个在线评价网站Epinions上的用户信任网络;社交网络[22]——在线社交网站Twitter上的用户间好友关系网络。上述网络的简要介绍见表1。
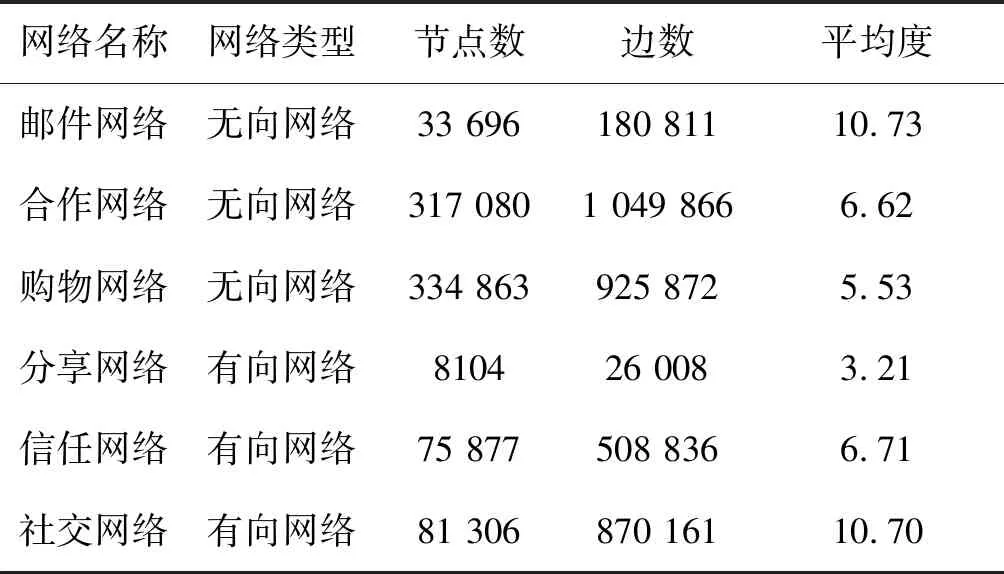
表1 六个真实网络数据基本性质表
3.3 度量准则
选取以下3个度量准则衡量算法的优劣性:种子节点传播范围,种子节点间的平均距离,以及冗余覆盖率。
传播范围是度量种子节点传播能力最直观的度量,定义种子节点S的传播范围FS为这些节点所能感染的节点数目。由于传播具有一定的随机性,需要通过多次数值仿真计算感染节点数目的均值。
集合内部节点间的平均距离可以从侧面反映这个集合的结构特性,定义种子节点间的平均距离为:
式中:|S|代表种子节点数目;dist(u,v)代表节点u到节点v的距离,即从u到v的最短路径跳数。
为了衡量种子节点传播范围的重叠程度,定义种子节点的冗余覆盖率为:
式中,FS为以S作为初始传播者时所能达到的传播范围,F{v}为仅以节点v作为初始传播者的传播范围。
3.4 实验结果
在实验中,设定恢复率q=1/k,感染率p=1.5q,其中k为网络的平均度。不同种子节点比例时的影响力传播范围如图2所示。从图2可以看出,快速评估算法的表现一致优于其他三种基准算法,并且随着种子节点数目的增加,快速评估算法的优势越来越明显。在6个不同类型的网络中,由快速评估算法选出的种子节点都具有更强的传播能力,体现了该算法的广泛适用性。
种子节点间的平均距离随着种子节点数量的变化如图3所示。由图3可知,种子节点间的相对距离越近,它们的传播范围相互重叠得越明显,会造成严重冗余,这对于信息传播是不利的。因此,一个好的算法找出的种子节点应当相互分散,即种子节点间的平均距离较高。在该指标下,快速评估算法依旧可以取得较为满意的结果,尤其是在邮件网络、信任网络、社交网络中,快速评估算法明显优于其他基准算法。在分享网络中,度中心找到的种子节点间的平均距离随着种子节点数目的增加呈现先减后增的趋势。事实上,这个结果并不反常,种子节点平均距离与种子节点数目之间并没有确定性的关系,而是与网络结构以及具体算法有关。分享网络是一个高度中心化的网络,由少数紧密相连的中心节点与大量边缘节点构成,呈现出一种明显的中心-边缘趋势。度中心算法会将网络的中心节点作为种子节点,由于中心节点是紧密相连的,因此随着节点数目的增加,种子节点间的平均距离会减少;当中心节点全部找出之后,度中心算法才会加入边缘节点,导致种子节点平均距离的逐渐增加。
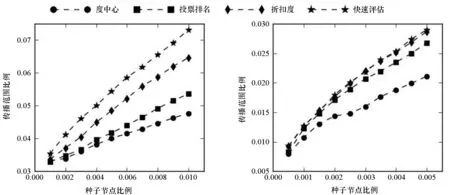
(a) 邮件网络(a) E-mail network (b) 合作网络(b) Collaboration network
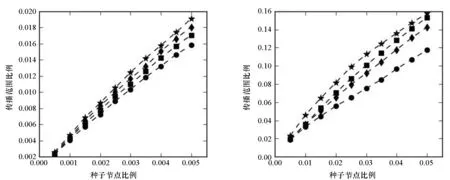
(c) 购物网络(c) Shopping network (d) 分享网络(d) Sharing network
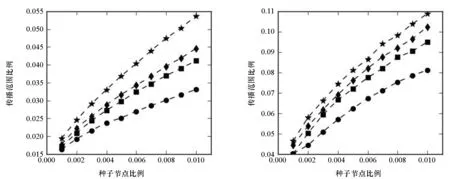
(e) 信任网络(e) Trust network (f) 社交网络(f) Social network图2 不同种子节点比例时的影响力传播范围Fig.2 Spreading scope with different fractions of seed nodes
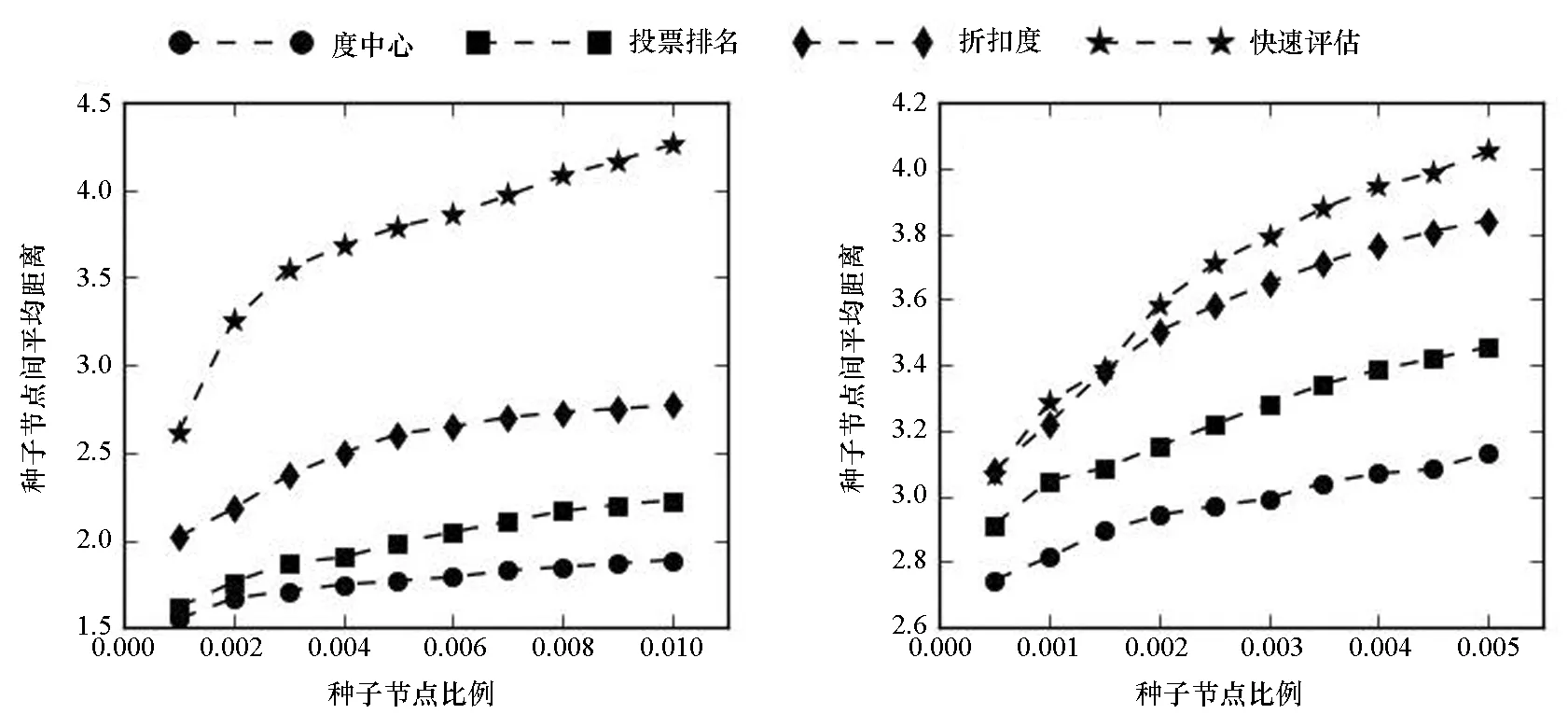
(a) 邮件网络(a) E-mail network (b) 合作网络(b) Collaboration network
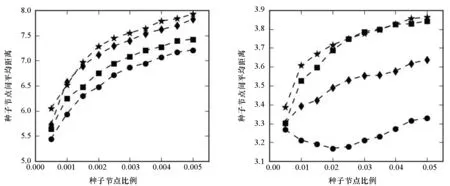
(c) 购物网络(c) Shopping network (d) 分享网络(d) Sharing network
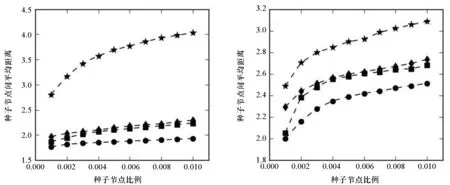
(e) 信任网络(e) Trust network (f) 社交网络(f) Social network图3 不同种子节点比例时的种子节点平均距离Fig.3 Average distance among seed nodes with different fractions of them
种子节点冗余覆盖率是衡量种子节点传播重叠程度的直观指标,冗余覆盖率越大,说明种子节点相互间的传播范围重叠程度越大,它们构成集群时的影响力损耗也越多。各算法在不同网络上的种子节点冗余覆盖率结果见表2,除了在分享网络上快速评估算法的表现略差于投票排名以外,在其他网络中该算法均能得到最优的结果。
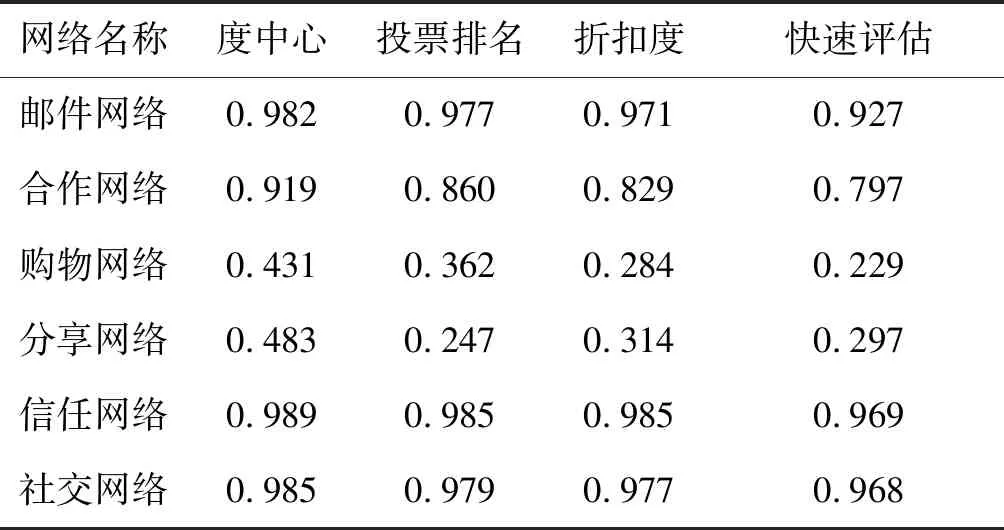
表2 种子节点冗余覆盖率
4 结论
本文实现基于种子集扩展的影响力极大化快速评估算法。在6个真实网络数据集上进行实证分析,验证了快速评估算法的有效性。而且快速评估算法具有很好的可拓展性。例如,对于节点传播能力异质的情况,可以将式(3)中的传播概率p替换为节点传播概率pu;当所考虑的网络为时序网络时[23-24],也可以将式(3)中的邻居集Γv替换为不同时间片r时的邻居集Γv(r)。仿照本算法中的推导过程,可以得到前述情况下的快速评估算法。在下一步的工作中,将对算法进行进一步优化,从图1中可以看出,算法对于传播范围的估计精度偏低,还有较大的改进空间。
