加权模糊C均值聚类算法实现BDS三频组合观测值优选

孟凡军，李树军，潘宗鹏，孙亦成，李忠盼

(1. 海军大连舰艇学院 军事海洋与测绘系， 辽宁 大连 116018； 2. 信息工程大学 地理空间信息学院， 河南 郑州 450001)

我国的北斗系统是全球首个全星座播发三频导航信号的卫星导航系统，三频载波相位组合观测值的优化选取是我国北斗系统优势发挥的关键[1-3]。一般来讲，全球导航卫星系统(Global Navigation Satellite System, GNSS)多频导航信号的出现为载波相位观测值提供了更多的组合方式，其中同时满足波长较长、电离层延迟较弱、观测噪声较小的多频组合为优选组合，传统上获取该类优选组合的方法一般为按照优选标准遍历搜索后进行人工筛选与分析，或者是运用经典的聚类算法实现多频观测系数组合的自动优选，但随着GNSS多系统的兼容性越来越高，多系统多频数据的应用将会越来越广，这时，传统方法便无法满足多频观测值优化选取中对高效性和可靠性的需求。因此，近年来GNSS多频载波相位组合观测值的优化选取一直为该领域的研究热点。

文献[4]引入模糊聚类理论，采用基于图论的最大树方法对GPS三频载波相位组合观测值进行分类，由此找到具有优良特性的组合；文献[5]利用基于相异度矩阵的自适应聚类算法，实现了GPS三频载波相位观测值的有效分类，并运用矩阵变换算法验证了该方法的有效性；文献[6]通过对样本中心与聚类中心距离的修正，获得合理的隶属度，并通过构建基于距离校正的聚类指标，自动获得最优聚类数；文献[7]构建了BDS/GPS四频载波相位组合观测模型，并采用传统搜索分析法选择了特性较好的BDS/GPS多频组合。

可见，目前对于单系统双频或三频的载波相位观测值优化选取方法已经比较成熟，但在多种聚类方法中，对于多频高维数据自动分类选取方法的研究仍然较少或方法传统，针对以上不足，本文以北斗卫星导航系统(BeiDou navigation Satellite system, BDS)三频载波相位观测值为例，在对其进行误差分析的基础上，采用了一种基于加权的模糊C均值混合数据聚类算法，通过将不同的权重值赋予同一维度上的不同簇集来影响聚类结果，有效解决了传统三频载波相位观测值筛选方式的不足，并提高了高维稀疏混合数据聚类算法的准确度。

1 BDS三频组合及优选标准

BDS原始观测量受很多因素的干扰，如卫星钟差、接收机钟差、电离层延迟、对流层延迟等，以上误差通过站、星间求双差可以大大削弱或消除[8-11]。

为表达方便，同一历元时刻，略去双差符号及卫星、接收机标识，BDS载波相位双差观测方程可以表示为：

φi=λiφi=ρ-μiI+εi+λiNi

(1)

式中：i=1，2，3，分别代表BDS三个频率；φi和φi分别对应以cycle为单位和以m为单位的双差载波相位观测值；λi(i=1，2，3)分别对应不同频率的波长；ρ表示卫地几何距离(以m为单位)；μi=(f1/fi)2(i=1,2,3)，为电离层延迟放大系数；I为B1频点的电离层延迟误差；Ni(i=1，2，3)为模糊度；εi(i=1,2,3)为观测噪声误差(以m为单位)。BDS三频载波的标准频率及波长见表1。

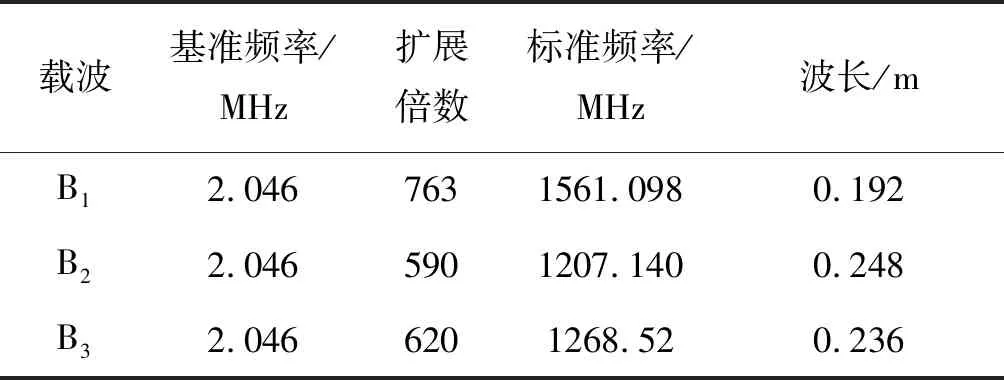
表1 BDS三频载波

对BDS三频载波进行线性组合可得三频载波相位组合观测值的观测方程为：

φc=αφ1+βφ2+γφ3…

=(α+β+γ)ρ-μcI+εc+λcNc

(2)

式中：φc为三频组合观测值(单位为m)；α，β，γ为组合观测系数。

由于组合观测量中卫地几何距离ρ不可随组合系数的不同而发生改变，须令

α+β+γ=1

(3)

因此三频组合观测方程可表示为：

φc=ρ-μcI+εc+λcNc

(4)

其中，

(5)

由式(5)可得，

Nc=(αλ1/λc)N1+(βλ2/λc)N2+(γλ3/λc)N3

(6)

式(6)中，令

(7)

则三频组合模糊度可表示为：

Nc=jN1+kN2+lN3

(8)

为保证组合模糊度依旧具有整数特性，要求j,k,l均为整数。则式(7)可变换为：

(9)

结合式(3)和式(9)可得，组合频率和波长分别表示为：

fc=jf1+kf2+lf3

(10)

(11)

通过以上推导，获得了三频组合观测值波长、电离层延迟系数以及观测噪声放大系数的表达式。为统一系数单位，得到以cycle为单位的电离层延迟误差的放大系数为：

(12)

假设BDS观测过程中三个频点观测精度相同，即σε1=σε2=σε3=σε。则以cycle为单位的组合观测噪声标准差σεc可以表示为：

(13)

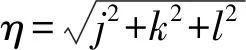
理论上来讲，BDS三频观测量可以形成无数组的组合，但要保证整周模糊度的快速解算，实现BDS高精度定位，优选组合需要满足长波长、弱电离层延迟、弱观测噪声的标准，具体分析可见文献[11]。

本文综合以上几项筛选标准，通过限定波长、电离层延迟系数、观测噪声放大系数这三个指标量，并将组合系数j，k，l的取值范围限定在[-10,10]以内，遍历搜索选出了一些特征值较优的线性组合见表2。

表2 BDS三频载波相位组合观测值

2 加权FCM算法实现观测值筛选

模糊C均值聚类(fuzzy C means)算法的主要目的是将包含有N个L维向量的数据集X划分为C个不同的簇，使得同一个簇中的数据对象比不同簇中的数据对象具有更高的相似度。结合本文应用需求，这里的维度理解为聚类指标的数目。

2.1 经典FCM算法概述

在FCM算法中，设待分类样本空间X={x1,x2,…,xi,…,xN}，该数据空间包含N个样本，其中每个样本都为L维向量，可以表示为xi={xi1,xi2,…,xik,…,xil}，其中xik代表样本xi的第k个特性值。

结合其定义，可设FCM算法的目标函数为：

(14)

由约束条件可知，FCM算法是一个反复循环迭代的过程，为了求得满足该条件的目标函数的极值，通过拉格朗日因子来构造新的目标函数，并结合对目标函数求极值的最优化条件，可得隶属度和聚类中心的计算公式为：

(15)

根据上述公式不断迭代求出满足条件的隶属度以及聚类中心[11]。

2.2 加权FCM算法流程

已有研究表明，经典的聚类算法在实现GNSS多频组合观测值上的有效性[3-6,11]，但在多频高维数据集的聚类过程中，经典的算法在应用上仍然存在两点不足：一是高维数据的属性之间互不相关或存在冗余，增加了分类的难度；二是高维数据空间分布相对稀疏，数据对象之间欧式距离的差异并不明显，难以利用传统的距离度量方式来划分簇[12-13]。

针对以上问题，本文结合Ahmad和Dey所提出的基于监督学习的距离计算方法[12]以及王振博所提出的基于加权模糊C均值的混合数据聚类算法[13]，采用基于加权欧氏距离的度量方式对不同维度的对象属性在簇内所占权重不同进行加权，并通过同一维度在不同簇上赋予不同的权重值来影响聚类结果，有效提高了高维混合数据聚类算法的准确度，文中相关定义见文献[13]。

改进后的FCM算法流程如图1所示。

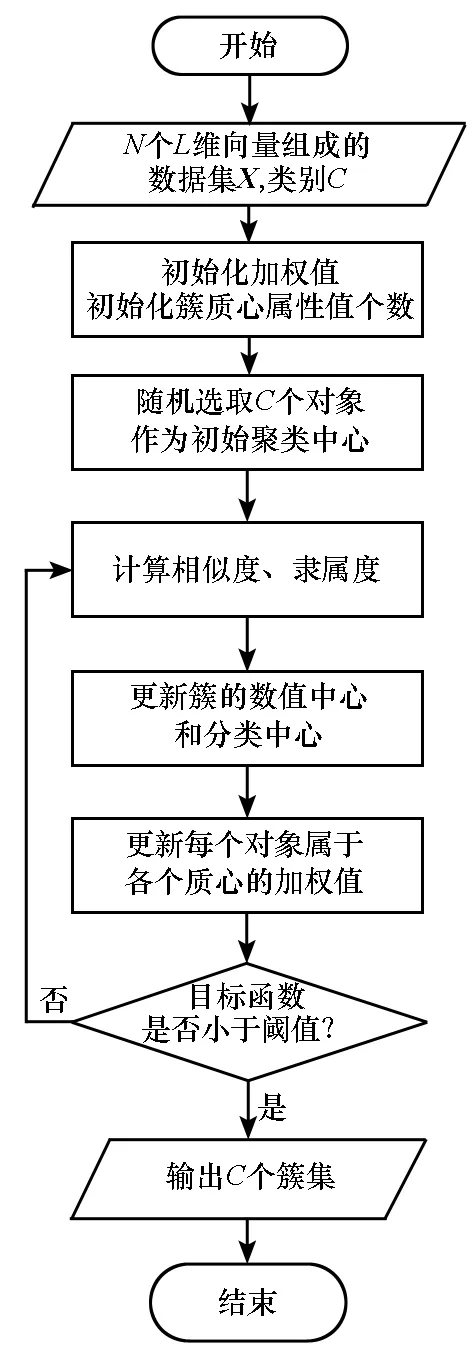
图1 改进FCM算法流程Fig.1 Flowchart of improved FCM algorithm

步骤1：首先给定一个由N个L维向量组成的数据集X以及所要分得的类别个数C(2≤C≤N)，自定义隶属度矩阵。结合表2，N=15，L=3，取C=4。设定模糊系数m(一般取2)和迭代停止阈值ε(一般取0.001至0.01)；设置迭代计数次数l，初始化聚类原型v(l)(l=0)。

步骤2：初始化加权值，初始化簇质心内对象的属性值个数。

步骤3：随即选择C个对象作为初始质心。

步骤4：计算对象到每个簇质心的距离。

步骤5：计算每个对象属于各个质心的数值隶属度。

步骤6：更新簇的数值质心和分类质心。

步骤7：更新每个对象属于各个质心的加权值。

步骤8：重复步骤4～7，直到目标函数的值与上一次的值小于阈值。

3 结果分析与算法验证

3.1 结果分析

基于上述改进的FCM算法，选取长波长、弱电离层延迟和低观测噪声三个维度的聚类指标，对表2中通过遍历搜索法所列出的15组优选BDS三频组合观测值进行了聚类分析，设定聚类类别数目C=4，迭代停止阈值ε为0.001[14]，聚类结果如表3和图2所示。

表3 模糊聚类结果

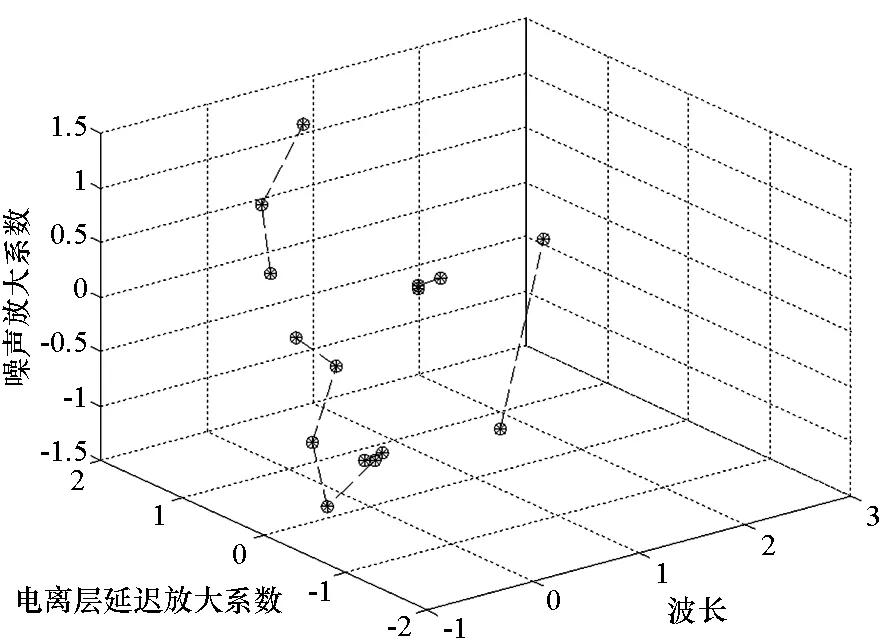
图2 模糊聚类输出结果Fig.2 Fuzzy clustering results

下面对每一类组合的适用范围进行分析。

第Ⅰ类组合，7(φ0，-1，1)、11(φ1，4，-5)的组合波长均大于4 m，以cycle为单位的电离层延迟误差放大系数和噪声观测系数均相对较小，满足最优选组合的标准。

第Ⅱ类组合，1(φ-1，-9，10)、2(φ-1，-8，9)、3(φ-1，-7，8)在表2各组合中波长较短，同时以cycle为单位的电离层延迟误差放大系数和观测噪声系数相对较大，不是优选组合。

第Ⅲ类组合，13(φ2，6，-8)、14(φ2，7，-9)、15(φ2，8，-10)波长较短，观测噪声系数较大，而电离层延迟误差放大系数特别小，因此这类组合比较适合应用于中长基线条件下整周模糊度的固定，但由于其波长较小，故在模糊度解算中应充分考虑到对流层延迟对定位的影响。

第Ⅳ类组合，4(φ0，-4，4)、5(φ0，-3，3)、6(φ0，-2，2)、8(φ1，1，-2)、9(φ1，2，-3)、10(φ1，3，-4)、12(φ2，5，-7)，该类组合优选性在第Ⅰ类组合与第Ⅱ类组合之间，电离层延迟误差放大系数和噪声观测系数相对第Ⅰ类组合较小，相比第Ⅱ类组合较大。其中，组合6(φ0，-2，2)和组合10(φ1，3，-4)在该类组合中波长相对较大，因此在短基线条件下，电离层延迟误差和对流层延迟误差可以通过组合双差解算大大削弱或消除，此时该类组合可以选用。

3.2 算法验证

为进一步验证文中优选组合的可靠性，本文采用无几何层叠模糊度解算(Cascading Integer Resolution, CIR)方法对实测BDS三频载波相位组合观测值进行模糊度的解算。

无几何CIR方法是无几何序贯取整算法的一种，其解算思路是根据不同的载波组合观测量的波长和相应的组合电离层误差、噪声误差特点，在保证组合观测量的综合误差小于1/2的组合波长情况下，对模糊度浮点解四舍五入直接取整固定，最后再确定原始的双差模糊度[15-17]。

略去双差符号以及卫星与接收机标识，双差伪距观测量可以表示为以下形式：

P=ρ+qpI+Tp+ep

(16)

式中：qp表示双差电离层延迟放大系数；Tp表示双差对流层延迟误差；I表示 B1频点上的双差电离层延迟误差；ep表示伪距观测噪声。

同时，用下标“E”“W”“N”分别表示超宽巷、宽巷和窄巷载波，那么以m为单位超宽巷、宽巷和窄巷载波相位组合观测量ΦEWL、ΦWL和ΦNL形式可以写成：

ΦE=λEφE=ρ-λENE-μEI1+TE+λEεE

(17)

ΦW=λWφW=ρ-λWNW-μWI1+TW+λWεW

(18)

ΦN=λNφN=ρ-λNNN-μNI1+TN+λNεN

(19)

无几何CIR方法的具体步骤如下。

步骤1：选取B3频点伪距观测量求解超宽巷模糊度，直接取整固定。

B3频点的双差伪距观测方程与组合系数为(0，-1，1)的超宽巷组合观测值ΦE双差观测方程如下：

P3=ρ+q3I+T3+ep3

(20)

ΦE=λφE=ρ-λENE-μEI1+TE+εE

(21)

由上两式可得超宽巷模糊度表达式为：

(22)

对于上式，略去对流层延迟误差、电离层延迟误差和观测噪声，并对其直接进行取整固定，超宽巷模糊度整数解可以表示为：

(23)

式中，round[·]为取整符号。

步骤2：将求解得到的超宽巷模糊度整数解作为已知值，求解宽巷模糊度。

将载波超宽巷组合观测量与载波宽巷组合观测量进行差分：

(24)

略去对流层延迟误差、电离层延迟误差和观测噪声，并对其直接进行取整固定，宽巷模糊度整数解可以表示成

(25)

步骤3：利用固定后的宽巷模糊度，求解原始载波的双差模糊度。

B1频点的载波双差观测方程为：

λ1φ1=ρ-λ1N1-μ1I1+T1+λ1ε1

(26)

将式(25)代入式(18)并结合式(26)可得 B1频点的双差模糊度为：

(27)

忽略电离层误差和噪声误差四舍五入取整得B1频点双差模糊度为：

(28)

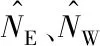
(29)

(30)

以上就是无几何CIR方法解算的全过程。

根据实测BDS观测数据，利用B1、B2、B3三个频点的观测值，测定不同组合的模糊度估值残差解算结果如图3～6所示。

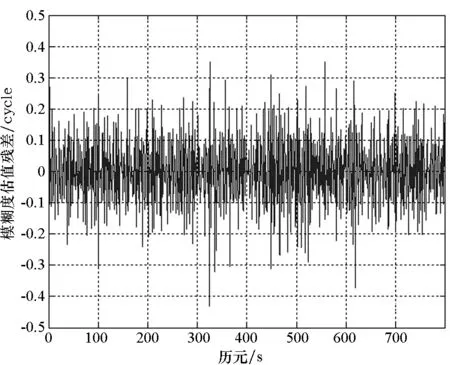
图3 (φ0，-1，1)组合模糊度估值残差Fig.3 Residual ambiguity difference of combination(φ0，-1，1)

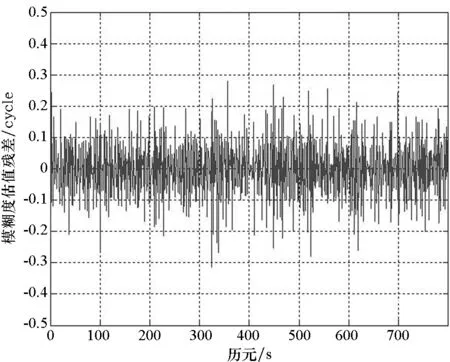
图4 (φ1，4，-5)组合模糊度估值残差Fig.4 Residual ambiguity difference ofcombination(φ1，4，-5)

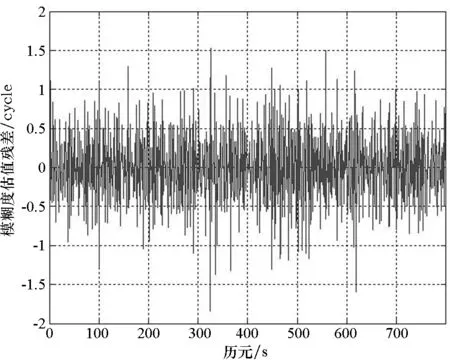
图5 (φ-1，-9，10)组合模糊度估值残差Fig.5 Residual ambiguity difference of combination(φ-1，-9，10)

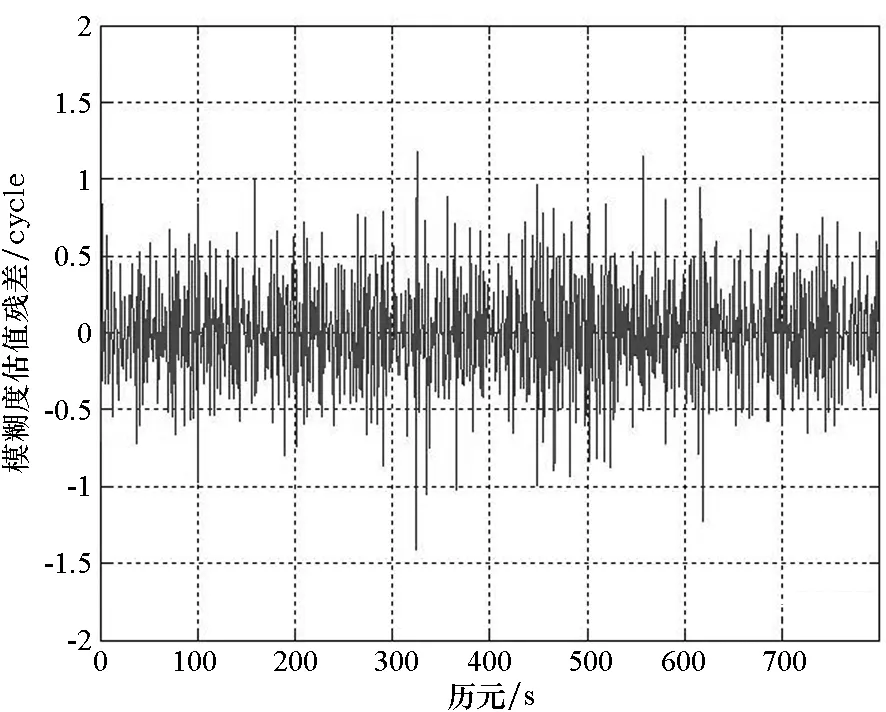
图6 (φ-1，-8，9)组合模糊度估值残差Fig.6 Residual ambiguity difference of combination(φ-1，-8，9)

由图3～6可知，组合1(φ-1，-9，10)和2(φ-1，-8，9)模糊度估值残差解算结果较大，最大接近2 cycle，在表2 所列优选组合中对模糊度的固定效率最低。组合7(φ0，-1，1)和11(φ1，4，-5)模糊度残差解算结果较小，在0.5 cycle以内，对模糊度的固定效率最高。由此可得，组合7(φ0，-1，1)、11(φ1，4，-5)的特性要比组合1(φ-1，-9，10)、2(φ-1，-8，9)好。

4 结论

本文引入三频载波相位组合观测值定义，对其进行误差分析，以长波长、弱电离层延迟、弱观测噪声作为优选组合系数的筛选标准，针对高维多频混合数据的聚类需求，采用基于加权的模糊C均值聚类算法，通过对同一维度的筛选标准在不同簇集上赋予不同的权重值，对传统遍历搜索法得到的部分组合进行分类，并对分类结果进行分析，确定了每一类组合的适用范围，最后结合北斗三频实测数据，利用无几何CIR算法计算组合模糊度估值残差，通过优选组合与非优选组合之间的比较证明，本文所选方法可以有效地对高频数据进行自动分类。