灵活的多层嵌套拉丁超立方体设计构造
2019-06-19段晓君王正明
徐 琎,段晓君,王正明,晏 良
(1. 国防科技大学 文理学院, 湖南 长沙 410073; 2. 国防科技大学 前沿交叉学科学院, 湖南 长沙 410073)
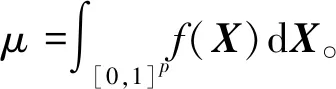
几乎所有的计算机试验都存在多种精度的情况,如何将这多种试验结合起来并充分利用所有数据信息是十分关键的问题。多种精度的试验有许多的应用,如飞行器设计相关试验等[6]。基于多种精度试验的建模方法也层出不穷,如贝叶斯修正方法[7]、贝叶斯分层建模[8]和计算机试验与实体试验的联合建模[9]等。在多种精度试验的设计选点部分,文献[10]提出了一种方法:嵌套拉丁方设计(Nested Latin Hypercube Designs, NLHD)。该设计保证了所有高精度的试验点在低精度试验中进行了同样的试验,这对后续试验的建模有很好的帮助[11],同时不同精度下的试验点集均为LHD。然而,SLHD及其若干后续研究(例如文献[12]和文献[13])均限制低精度试验的试验次数必须是高精度的倍数。这就导致在具体的试验中,试验次数会有诸多限制。文献[14]和文献[15]介绍了结构灵活的设计,分别为序贯设计(Sequential Designs, SD)和广义嵌套拉丁超立方体设计(General Nested Latin Hypercube designs, GNLH),但SD方法的均匀性不够,其较低精度的试验点在大多数情况下不是LHD,而GNLH只能构造两层的嵌套设计。因此,对于三种或三种以上精度的计算机试验,现有工作无法给出结构灵活的嵌套拉丁超立方体设计。
本文介绍一种结构灵活的多层嵌套拉丁超立方体设计(Multi-layer Nested Latin hypercube Designs, MND),其试验设计点数可以灵活选取,同时每类精度试验的试验点均有很好的一维投影均匀性。
1 MND的结构与性质
1.1 MND的构造方法
下面对MND构造算法中使用到的符号进行说明。Zn表示整数集合{1,…,n}。对于向量v,v(i)表示其第i个元素。对于矩阵A,A(i,j)为第i行j列元素。
对于给定的整数u≥3,0
对于j=1,…,u-1,vj为lj维随机向量,其中vj(1)服从Zlj+1/lj上的离散均匀分布;对于i=2,…,lj,vj(i)=Mlj+1/mj+1,lj+1/lj(ri,vj(i-1)),其中ri服从Z(lj+1/lj)-(lj+1/mj+1)+1上的离散均匀分布。
容易看出,该算法有效需满足的条件是:对于i=1,…,u-1,mi+1是mi的倍数或mi+1≥li。由于实际应用中,高精度与低精度试验的试验点一般差距较大,故大多数的试验可以满足上述两个条件。同时,对于j=1,…,u-1,根据lj维向量vj的定义可知,其元素均属于Zlj+1/lj。再由τ1的元素均属于Zm1可以得出τj+1的元素均属于Zlj+1,因

算法1 构造MND
此,算法1步骤8中元素vj(τj(k))对任意的j=1,…,u-1均存在。下面用一个例子来更好地说明该算法的流程。
例1对于u=3,m1=2,m2=5,m3=13,p=1,随机生成τ1=(2,1)T,且v1来自矩阵M2,5。随机构造后得向量v1=(4,2)T,则
τ2(1)=5(τ1(1)-1)+v1(τ1(1))=7
同理,τ2(2)=4。由算法1步骤10随机生成τ2剩余的3个元素,得τ2=(7,4,9,2,6)T。v2来自矩阵M10,13。随机构造后得向量v2=(1,13,10,8,6,4,2,2,12,9)T。则
τ3(1)=13(τ2(1)-1)+v2(τ2(1))=80
同理,得到
τ2=(80,47,116,26,69,124,31,95,15,90,105,60,3)T
则嵌套向量d=(τ3-ε)/130。图1显示了嵌套向量d,即MND的一维投影均匀性。由图可知,对任一层,其均可满足在任一区间中有且仅有一个点。
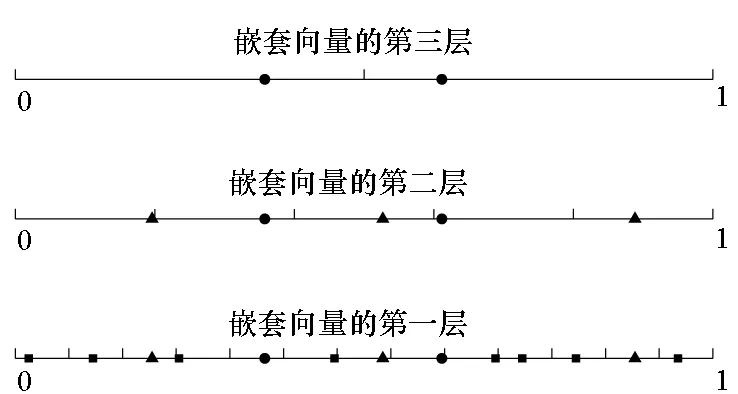
图1 MND的一维均匀性Fig.1 One-dimensional uniformity of MND
1.2 MND的统计性质
进一步,对于MND的性质有如下定理。
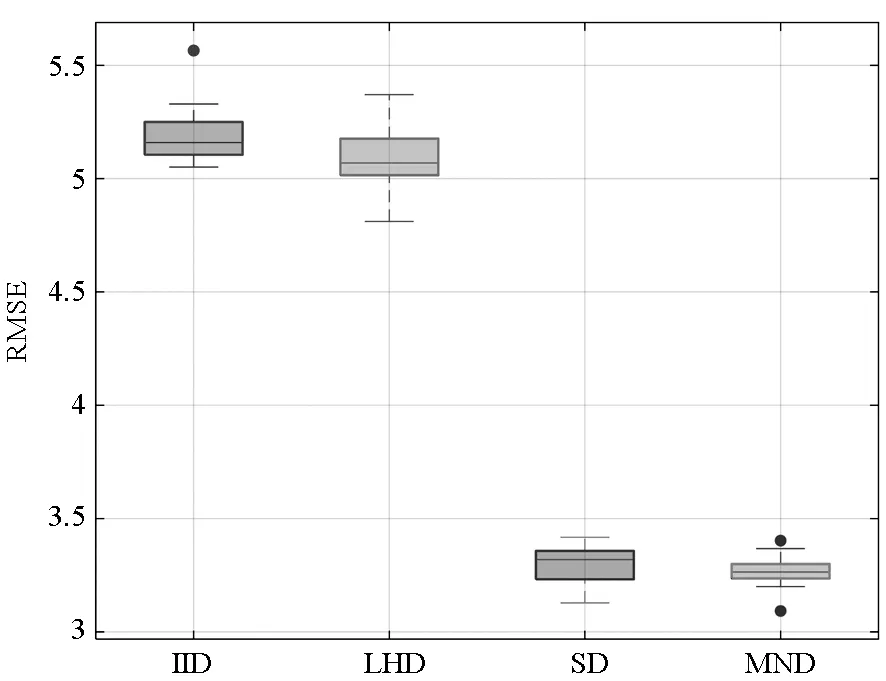
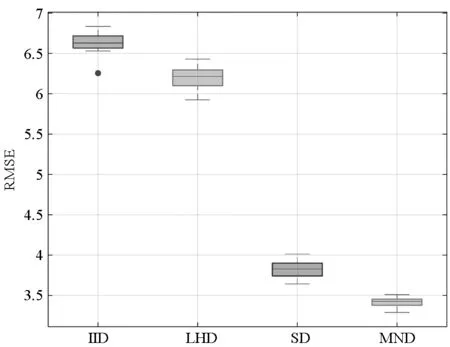
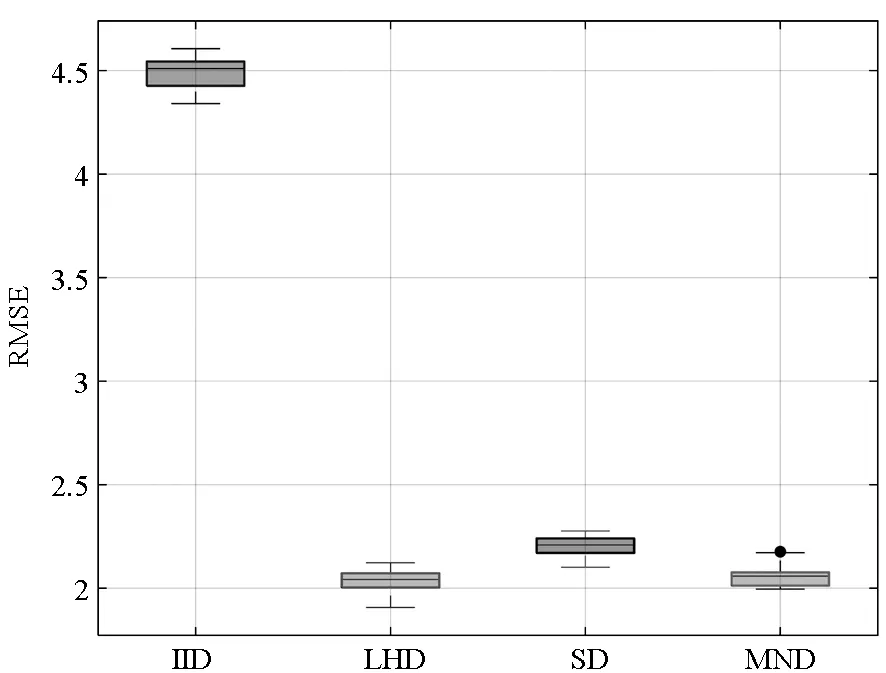
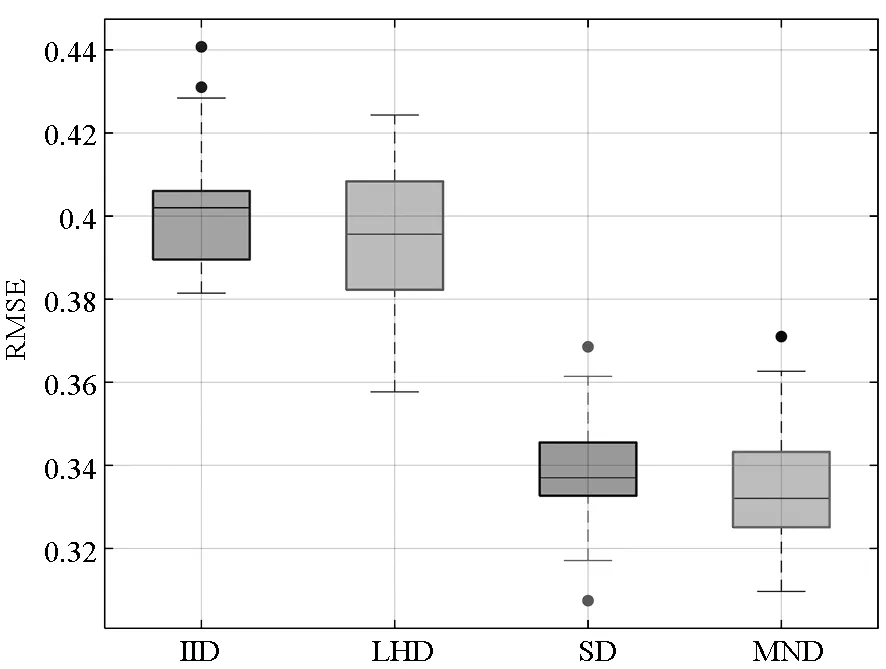
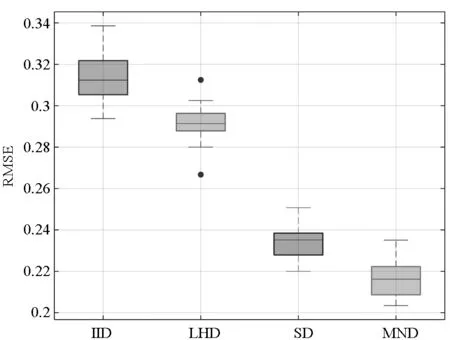
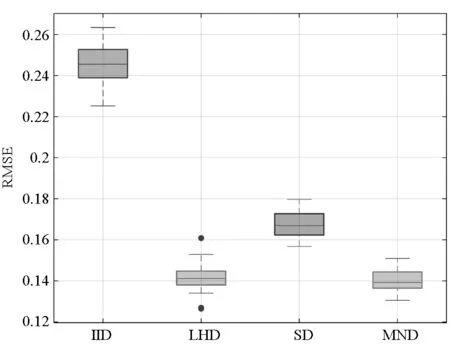
定理1对于给定的整数u≥3,0 1)对于任意的k=1,…,u及i,j=1,…,mu且i≠j,有 「τ(i)mk/l⎤≠「τ(j)mk/l⎤ 2)对于i=1,…,mu,a=1,…l,有 P{τu(i)=a}=1/(mul) 证明:类似文献[15]中命题1的证明,易知该定理成立。 □ 关于MND设计D=(d(1),…,d(p))有如下两个定理。 定理2对于i=1,…,u,j=1,…,p,{d(j)(1),…,d(j)(mi)}满足在任一区间[0,1/mi),…,[(mi-1)/mi,1)中有且仅有一个设计点。 证明:由定理1 第1部分可知。 □ 定理3对于i=1,…,mu,{d(1)(i),…,d(p)(i)}服从[0,1)p上的均匀分布。 证明:由定理1 第2部分可知。 □ 对于运行次数分别为m1,…,mu的多种精度试验,有四种方法可对其进行处理,依次为: 1)独立同分布抽样(Independent and Identically Distributed sample, IID):选取mu行的独立同分布抽样,利用其前mi行处理第i个试验。 2)LHD:选取mu行的拉丁超立方体设计矩阵,利用其前mi行处理第i个试验。 3)文献[14]的方法SD。 4)多层嵌套设计MND。 1)M1: 2)M2: 其中,M1中的函数h1(x)由文献[16]提出,M1中h2(x)和h3(x)来自文献[17]。M2中h1(x)被称为borehole函数[18],在计算机试验中经常选其作为黑箱函数[13,16,19]。在M2中代替低精度函数的h2(x)和h3(x)由文献[13]构造。对于不同方法生成的设计矩阵D,其前m1试验点对应模型h1(x),前m2试验点对应模型h2(x),整个设计矩阵对应模型h3(x)。图2和图3分别为在M1和M2下不同方法估计μi的均方误差。其中选定的参数为m1=2,m2=5,m3=13,每类试验进行2000次,得出各方法的RMSE后进行对比。从两图中可以得到:①IID方法的均方误差最大;②在高精度试验中,SD和MND均比LHD表现好,其原因在于这两者的子矩阵比LHD的子矩阵有更好的均匀性;③在估计μ1时, MND与SD有几乎相同的均方误差;④在估计μ2和μ3时,MND比SD有更小的均方误差,原因在于MND比SD在整体上有更好的均匀性;⑤在估计μ3时,MND和LHD有相同的RMSE,这是因为MND和LHD的全矩阵有相同的均匀性。 (a) M1中模型h1(x)(a) Model h1(x) in M1 (b) M1中模型h2(x)(b) Model h2(x) in M1 (c) M1中模型h3(x)(c) Model h3(x) in M1图2 M1下各方法RMSE比较Fig.2 RMSE comparison of the different schemes on M1 本文构造了灵活的多层嵌套拉丁超立方体设计,与一般的嵌套设计相比,该方法在参数选取上具有很强的灵活性。与SD相比,该方法各层在一维上均可达到更好的均匀性,这使得在估计模型均值时,其估计方差更小。两个算例也体现了多层嵌套拉丁超立方体设计的性质。虽然第1节中给出的算法也有其局限性,即对于i=1,…,u-1,mi+1是mi的倍数或mi+1≥li需满足,但由于实际应用中,高精度与低精度试验的试验点一般差距较大,故大多数的试验可以满足上述两个条件。 (a) M2中模型h1(x)(a) Model h1(x) in M2 (b) M2中模型h2(x)(b) Model h2(x) in M2 (c) M2中模型h3(x)(c) Model h3(x) in M2图3 M2下各方法RMSE比较Fig.3 RMSE comparison of the different schemes on M22 算例
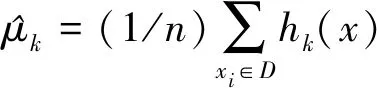
3 结论