阵列雷达自适应多零点单脉冲群目标测角算法
2019-06-19王罗胜斌徐振海刘兴华王国玉
王罗胜斌,徐振海,刘兴华,董 玮,王国玉
(国防科技大学 电子科学学院 电子信息系统复杂电磁环境效应国家重点实验室, 湖南 长沙 410073)
位于同一距离单元、角度单元和多普勒单元内,在任何一维度,利用常规线性处理方法都难以分辨的多个目标集合称为群目标[1],学术界也称为不可分辨目标。在雷达探测领域,尤其在远程预警中,群目标现象普遍存在。在防空背景下,编队飞机可构成群目标;在精确制导背景下,飞机和拖曳式诱饵也可构成群目标;在反导背景下,弹道导弹突防时释放的有源或无源诱饵、箔条以及分离过程中产生的碎片等亦可构成群目标。群目标特性复杂,严重影响雷达探测。精确测量群目标角度是跟踪、识别群目标的前提。
单脉冲技术具有测角精度高、工程易实现等优点,但在群目标条件下,测量的角度与任一目标均不对应,并随着目标间相对幅度和相位剧烈“抖动”,甚至超出雷达角度范围,这种测量误差可能导致跟踪丢失[2]。针对此问题,Sherman等[2]、Lee等[3]将群目标单脉冲比作为确定量,提出利用两个脉冲的和、差信号求解双目标角度的方法,但此方法需要两个独立的脉冲。Zheng等[4]在此基础上提出利用四象限单脉冲分辨群内双目标方法,并推导了矩形阵列的双目标角度闭式解。Blair等[5-8]将群目标单脉冲比作为随机量,重点分析其统计特性,针对两个瑞利目标提出了基于瞬时匹配的角度估计方法。在此基础上,Sinha等[9]推导了Swerling Ⅰ型和Swerling Ⅲ型目标的似然函数,用栅格搜索得到角度的极大似然估计,但计算量巨大。最近,Glass等[8]提出利用相邻距离采样提高分辨精度。然而,单脉冲雷达处理自由度少,大多数方法需要多个脉冲增加时间上的处理维度,难以拓展至多个目标情况,严重限制了群目标的测角性能。
另一种思路是利用阵列雷达多样式、多维度的信号处理方法实现群目标测角。众多方法中参数法[10](极大似然估计)因为具有更强的鲁棒性而应用广泛。早在20世纪70年代,White[11]针对海面低角目标出现镜面反射时难以跟踪的问题,基于极大似然估计原理提出了阵列双零点单脉冲技术,并给出了该技术应用至空间多目标的思路与应用框架,但没有进一步的研究报道。文献[12]将双零点单脉冲技术进行完善,只需较少的计算量就能实现低角目标跟踪。文献[13]将此技术应用至空间双目标情况,获得了良好的分辨效果。
1 信号模型与估计方法
1.1 群目标回波模型
N元均匀半波长线型阵列雷达主瓣内存在M个目标,接收信号为多个目标回波的线性叠加。经过信号放大、变频、采样等处理,群目标回波模型可表示为:
(1)
下标i表示第i个目标;Ai表示回波复幅度;s(ui)表示阵列导向矢量,
(2)
j表示纯虚数;ui=sinθi为目标角度的正弦空间坐标,θi为目标与阵面法向的夹角,ui∈[-u3 dB/2,u3 dB/2],u3 dB为雷达主瓣波束宽度;n∈CN×1表示阵列接收机热噪声矢量,服从零均值高斯分布,热噪声功率为σ2。当M=1时,信号模型退化为单目标情况。
1.2 极大似然估计
将群目标回波模型改写为矩阵形式:
x=Sa+n
(3)
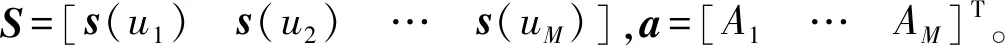
p(x|u1,…,uM,A1,…,AM)
(4)
当回波数据与假设模型之间的均方误差最小时似然函数最大,所以极大似然估计可表示为:
(5)
复幅度a的极大似然估计实际上是最小二乘问题[14],估计值为:
(6)
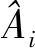
目标函数Q关于u1,…,uM分别求偏导,得到方程组:
(7)
式中,dH(ui)=ds(ui)/dui为信号矢量关于角度的导数,与导向矢量正交,即dH(ui)s(ui)=0。
式(7)为非线性方程组,难以直接求解,必须通过迭代逼近求解[11]。一种求解思路是利用凸优化方法求解目标函数Q的极小点,但此类方法需要求解梯度,计算量巨大,并且迭代步长难以控制;另一种思路是利用多维单脉冲测量[15]估计目标角度,这种方法是阵列单脉冲处理的一种多维扩展,计算量小。本文将采取第二种思路,实现群目标的角度估计。
2 群目标角度估计方法
2.1 自适应多零点单脉冲测量
将式(7)可改写为:
(8)
由于dH(ui)s(ui)=0,式(7)可以进一步写为:
(9)
将式(6)代入式(9)可得:
Re{dH(ui)[I-S(SHS)-1SH]x}
=Re{dH(ui)PS⊥x}=0
(10)
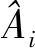
利用数字波束形成技术生成M套单脉冲系统,分别指向ub1,ub2,…,ubM。令
(11)
(12)
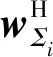
(13)
(14)
其中,Sb=[s(ub1)s(ub2)…s(ubM)]。
每套单脉冲系统和、差接收波束的方向图分别为:
(15)
(16)
由式(13)~(16)可以推出:
Σi(ubj)=0j≠i;j=1,2,…,M
(17)
Δi(ubj)=0j=1,2,…,M
(18)
式(17)、式(18)说明每套单脉冲系统会在其他系统的波束指向处自适应形成零点,保证和波束输出能量最大,抑制其他目标信号的影响,故将此类单脉冲测量称为自适应多零点单脉冲测量。
2.2 迭代优化——步长加权法
根据自适应多零点单脉冲的测量结果无法直接测量目标角度。以第一套单脉冲系统为例,输出的群目标单脉冲比为:
(19)
式中,K1表示第一套单脉冲系统的鉴角斜率。可以看出,多维单脉冲系统输出的角度实际上是群目标的复指示角[2],不能像传统单脉冲一样“一步”测角,只能通过更新迭代波束指向不断逼近目标角度,所以这是一种次优估计[17]。
当目标数为2时,根据单脉冲系统测量的角度,文献[12-13]提出如式(20)所示角度迭代方式。
(20)
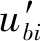
双目标条件下,用复指示角直接更新波束指向能够迅速收敛于目标角度,主要原因为:对于第一套单脉冲系统,和、差波束接收的主要能量来自第一个目标,自适应零点抑制了第二个目标的干扰,更新后的波束指向更逼近于第一个目标,使得接收到第二个目标的能量越来越弱。然而,对于多个目标,更新后的波束指向无法锁定同一目标,导致迭代不收敛。
从优化的角度来看,迭代步长过大导致双零点测角无法直接扩展至多个目标,必须自适应调整迭代步长。当波束指向偏离目标时,各单脉冲系统形成的零点也偏离目标,无法起到抑制的效果,此时更新步长应该较小;当波束指向接近目标时,抑制效果明显,复指示角度接近真值,此时更新步长应该较大。
通过以上分析,提出一种步长加权的方式改善迭代过程,其思路为:用目标函数Q反映波束指向偏离目标的程度,从而确定权值w的大小。此处,令调整步长的权值w与目标函数的数量级lgQ成正比关系,即目标函数每下降一个数量级,步长权值相应地线性增加。步长权值的表达式为:
(21)
式中,Q0表示用波束指向初值计算得到的目标函数取值,ε为收敛误差,w0为权值初始点。权值w是关于Q的函数,Q越小,波束指向越接近目标。w0与信噪比有关,信噪比越高,w0越大。
利用加权的方式在式(20)的基础上改进波束指向更新:
(22)
2.3 群目标角度估计算法流程
根据以上对自适应多零点单脉冲以及波束指向迭代更新的分析,提出自适应多零点单脉冲群目标测角算法,算法流程如图1所示。
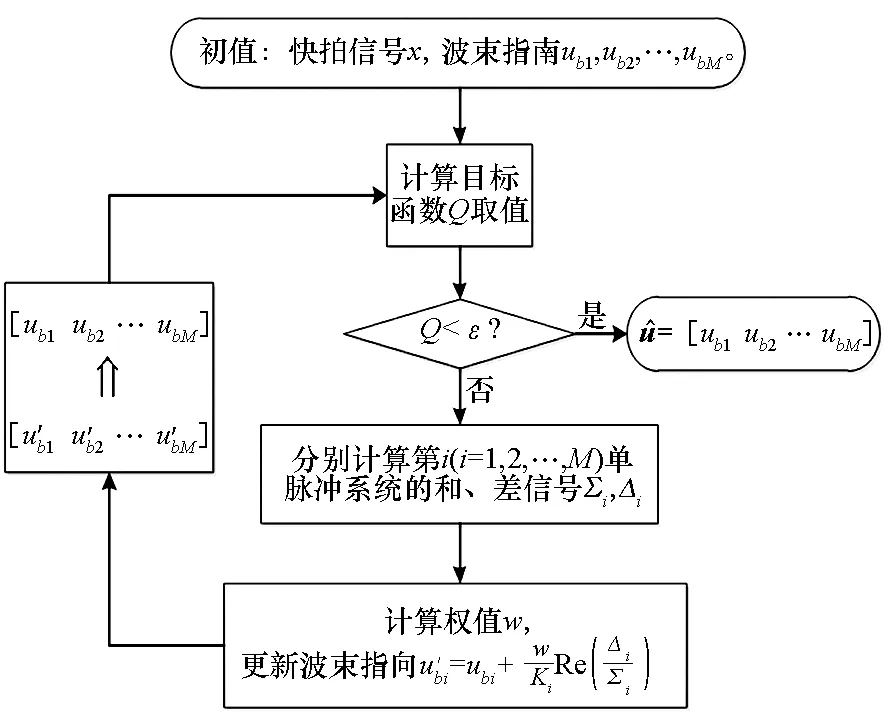
图1 算法流程图Fig.1 Flowchart of algorithm
图2给出了自适应多零点单脉冲测角算法、交替投影法[18]、步长回溯法[19]三种方法在三个目标条件下(u1=-0.2u3 dB,u2=0.1u3 dB,u3=0.45u3 dB)的迭代过程。由图可知,多零点单脉冲测角算法只需300次左右的迭代就能实现高精度的角度估计,而交替投影法需要4000次左右的迭代,步长回溯法虽然能迅速收敛,但估计值与真值存在明显偏差。相比之下,自适应多零点单脉冲测角迭代次数更少,并且只需计算单脉冲比,计算量远小于梯度的计算。因此,该测角算法更易于工程实现。
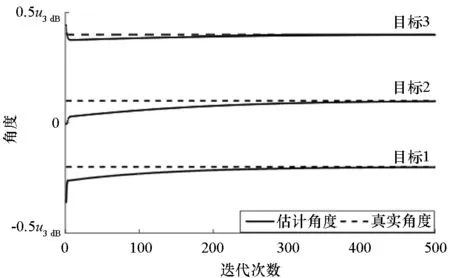
(a) 自适应多零点单脉冲测角算法(a) Angular estimation of adaptive multi-null monopulse
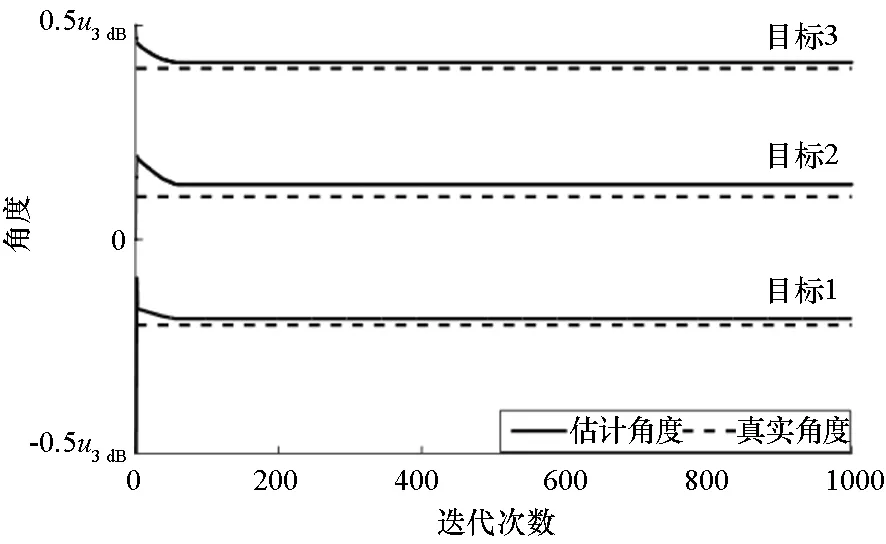
(b) 交替投影法(b) Alternating projection method
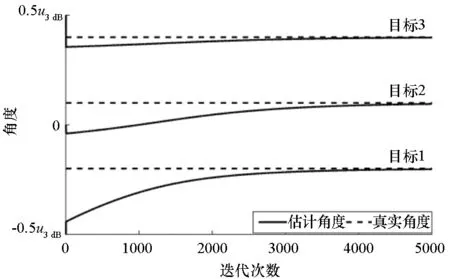
(c) 步长回溯法(c) Step backtracking method图2 迭代收敛过程Fig.2 Iterative convergence process
3 仿真分析
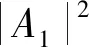
设最大迭代次数为1000,收敛误差ε=10-12,图4给出了多种信噪比下不同目标函数对应的步长权值。
定义角度估计均方根误差(Root Mean Square Error, RMSE)为:
(23)
式中,E[·]表示取均值。
进行1000次Mont Carlo仿真,分析算法性能。在假设已知准确群目标数的条件下,将本文方法与前后空间平滑的多重信号分类法(Front Back
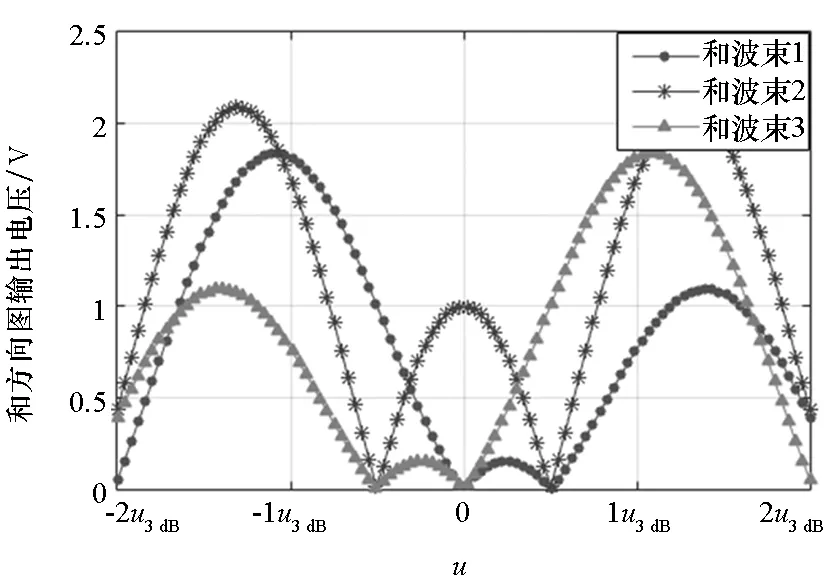
(a) 和波束方向图(a) Sum beampattern
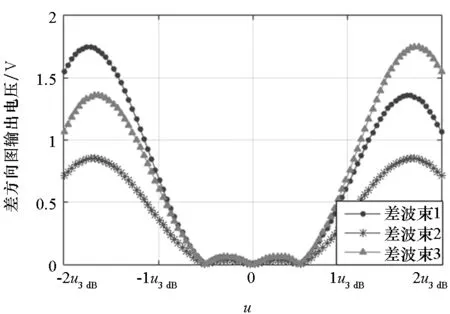
(b) 差波束方向图(b) Difference beampattern
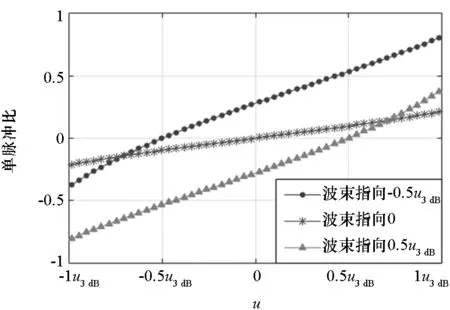
(c) 单脉冲比鉴角曲线(c) Monopulse ratio curve图3 自适应多零点单脉冲和、差方向图以及单脉冲比鉴角曲线Fig.3 Sum/difference beampattern and monopulse ratio curve of adaptive multi-null
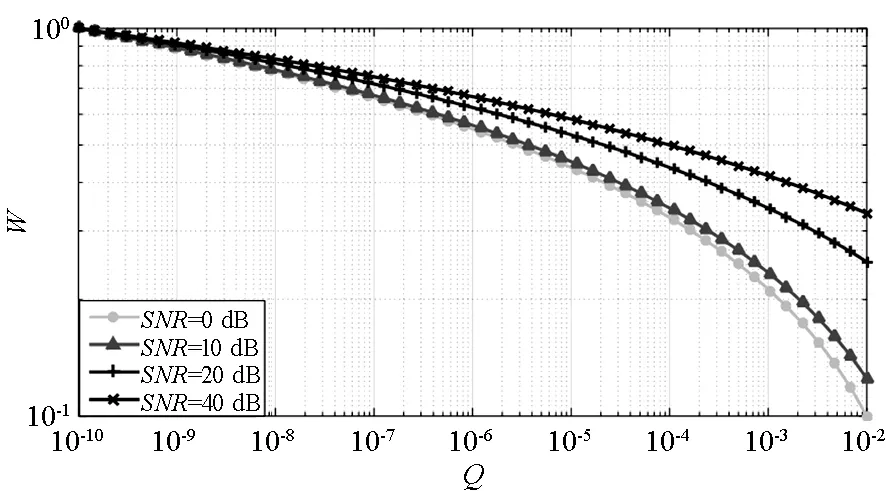
图4 步长权值曲线Fig.4 Weighted step
Spatial Smoothing MUltiple SIgnal Classfication, FBSS-MUSIC)[14](空间平滑预处理的MUSIC算法)以及交替投影法进行对比实验。
3.1 测角精度与信噪比的关系
在该实验中,设定三个目标的角度分别为u1=-0.2u3 dB、u2=0.1u3 dB、u3=0.45u3 dB,复幅度分别为A1=1、A2=0.9ejπ/4、A3=ej3π/2。图5给出了三种算法的RMSE与SNR关系曲线。
可以看出:随着信噪比的增大,三种算法的测角精度提高,这是普遍规律;在高信噪比条件下,本文方法的测角性能与交替投影法相近,测角误差约为0.15u3 dB;在低信噪比条件下,本文方法测角性能更优,并且精度远高于FBSS-MUSIC,说明本文方法的鲁棒性更强;FBSS-MUSIC在低信噪比条件下性能很差,其主要原因是MUSIC等子空间方法不适用于相干源,在单次快拍条件下需要空间平滑预处理,但这种处理损失了空间分辨率,难以精确估计信号协方差矩阵。
3.2 测角精度与角度间隔的关系
在该实验中,设定三个目标关于阵列法向对称分布,角度分别为u1=-Δu、u2=0、u3=Δu,复幅度分别为A1=1、A2=0.9ejπ/4、A3=ej3π/2,信噪比SNR=30 dB。图6给出了三种算法RMSE与Δu的关系曲线。
可以看出:随着目标角度间隔的减少,测角精度下降,这是群目标测角的特有规律;当目标角度间隔低于0.25u3 dB时,三种方法都无法精确测角;实际上,若目标角度间隔非常小,群目标可作为单个目标处理。
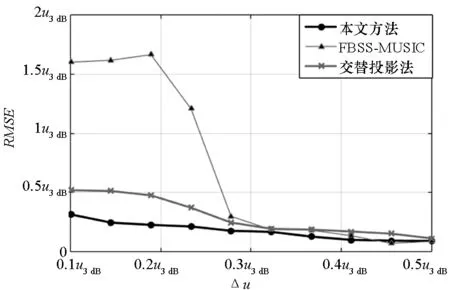
图6 测角精度与角度间隔的关系Fig.6 Performance of angular estimation versus Δu
3.3 测角精度与相对复幅度的关系
在该实验中,假设群内存在一个大目标与两个小目标,设定三个目标角度分别为u1=-0.2u3 dB、u2=0.1u3 dB、u3=0.45u3 dB;信噪比SNR=30 dB;三目标的相对复幅度分别为A1=1、A2=pejΔφ、A3=pej-Δφ。令ρ=pejΔφ,只考虑FBSS-MUSIC与本文方法,图7给出了两种算法RMSE与ρ的关系。可以看出:随着目标幅度差异的增大,FBSS-MUSIC的测角精度降低,但对目标的相对相位影响不大;而本文方法恰好相反,在目标相对相位为0时测角精度最低,在目标幅度差异较大时仍能保持较高的测角精度。
对于单次快拍,运用子空间方法之前需要进行空间平滑得到满秩的协方差矩阵,这种预处理消除了目标之间的相位信息,测角精度只与目标幅度有关。当目标幅度差异较大时,小目标极易被大目标“遮掩”,在空间谱上难以分辨,严重影响测角精度。而运用参数法时,所有的参数均由极大似然估计得到,大目标对小目标的“遮蔽”影响得到极大的弱化。所以,当目标幅度相差较大时,参数法具有比子空间方法更好的测角性能。
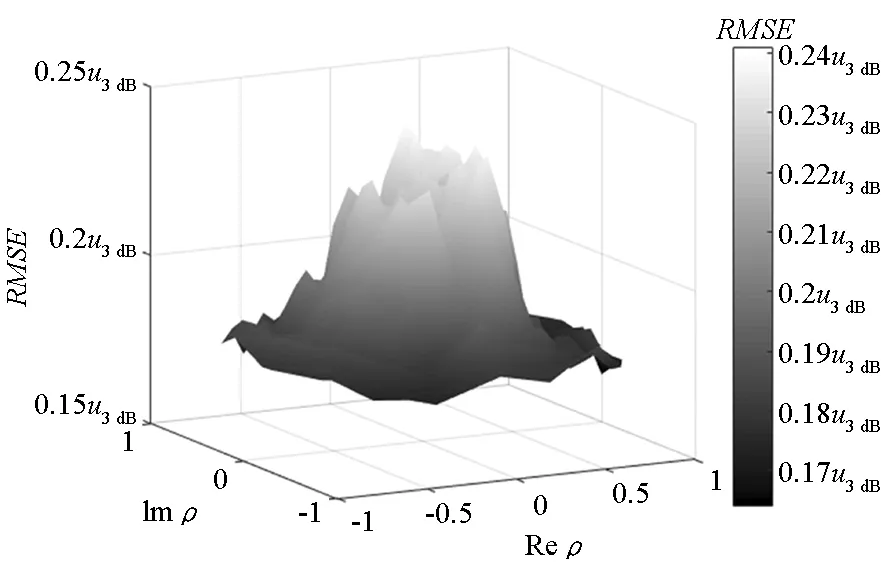
(a) 对比算法(a) Algorithm for comparison
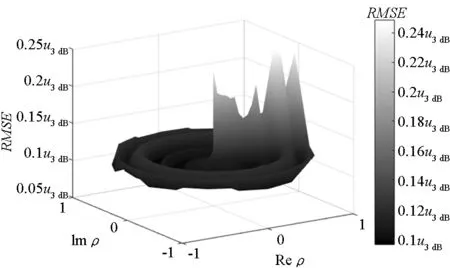
(b) 本文算法(b) Proposed algorithm图7 测角精度与相对复幅度的关系Fig.7 Performance of angular estimation versus relative complex amplitude
3.4 测角精度与目标数的关系
在该实验中,考虑目标数从1增至5。设定多个目标关于阵列法向对称分布,回波功率相同,信噪比均为SNR=30 dB,相邻目标的角度间隔均为Δu=0.25u3 dB,相位差均为Δφ=π/6。图8给出了本文方法RMSE与目标数的关系曲线。
可以看出:随着目标数的增多,测角精度急剧降低;当目标数为1时,自适应多零点单脉冲退化为阵列幅度和、差单脉冲,测角精度非常高;当目标数超过4时,估计误差接近于半个波束宽度。这是由于目标数增多,需要估计的参数更多,估计精度下降,当群目标数目较多时,只有在非常高的信噪比条件下才能实现精确测角。
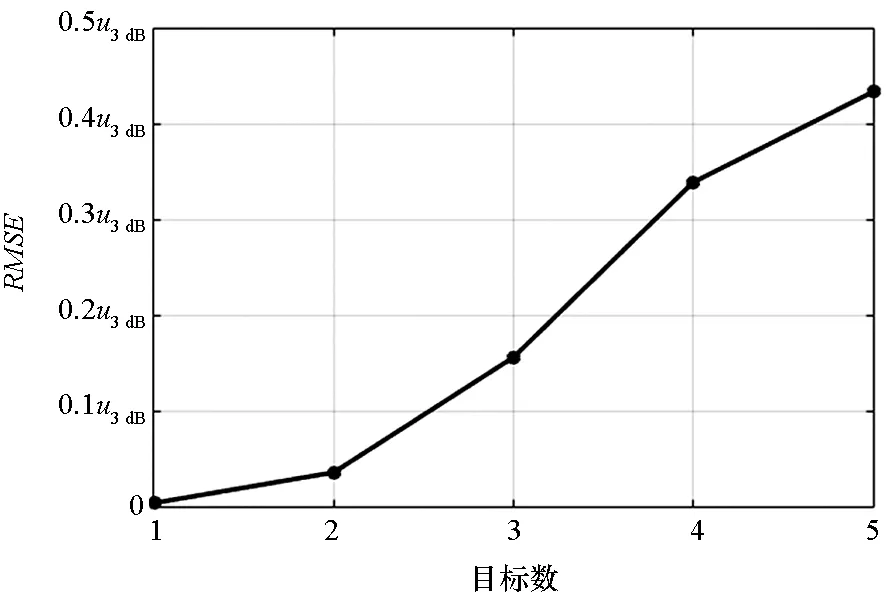
图8 测角精度与群目标数的关系Fig.8 Performance of angular estimation versus unresolved target number
4 结论
仿真结果表明:在较高信噪比条件下,本文所提算法可以精确测量三个目标角度,测角精度约为0.15倍波束宽度;但当群目标数较多或者目标相位差接近于0时,算法性能严重下降。在目标幅度相差较大的条件下,本文方法具有比子空间方法更好的测角性能。
无论是子空间方法还是参数化方法,都需要目标数目的先验信息,当目标数目估计不准时,测角性能将急剧下降。在群目标数目估计方面,参数化方法可以与目标参数模型匹配方法[15]相结合,通过估计的目标参数修正估计的目标数,以获得更好的目标数估计性能。
