体验求值题型，感受“三角”魅力

■刘德龙

面对三角函数的求值、化简和证明问题，许多同学感觉无从下手，而三角恒等变换是三角函数的求值、求角问题中的难点和重点，其难点在于：一是如何熟练掌握众多公式，二是如何根据三角函数的形式去选择合适的求值、求角方法。三角函数求值问题常见的题型有三种：给值求值、给角求值、给值求角。

题型一：给值求值

例1已知则tan 2α=____。

解：（方法1）由解得或因此或tanα=3。

点评

方法1是常用解法，通过联立方程组，再利用二倍角的正切公式求解。方法2优于方法1，方法2是利用二倍角的正弦、余弦公式变形求解。

例2已知则cosβ的值为____。

解：因为所以又因为，所以由于所以

点评

解答三角函数的给值求值问题，关键是把所求角用已知角表示。已知角为两个时，所求角一般表示为已知角的和或差关系；已知角为一个时，所求角一般表示为已知角的倍数关系、互余或互补关系。

题型二：给角求值

例3化简____。

解：原式

点评

通过变换三角函数名称达到减少三角函数种类的目的，其手法通常有“切化弦”“升幂与降幂”等。

例4（1+tan18°）·（1+tan27°）的值是（ ）。

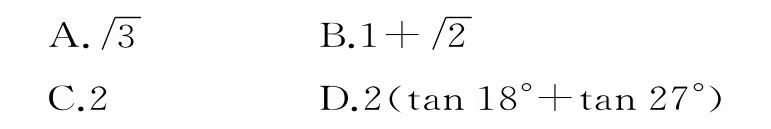
解：由题意可知27°+18°=45°，所以，可得tan27°+tan 18°=1-tan 27°tan 18°。

故原式=1+tan 18°+tan 27°+tan 18°·tan 27°=1+tan18°tan27°+（1-tan 18°·tan 27°）=2。应选C。

点评

把所求问题中的非特殊角向特殊角转化是解答本题的突破口。

例5sin 15°+sin 75°的值是____。

解：（方法1）sin15°+sin75°=sin15°+

（方 法 2）因 为 （sin15°+sin75°）2=（sin 15°+cos15°）2=1+2 sin15°cos15°=1，又sin 15°＞0，sin 75°＞0，所以sin 15°+sin 75°＞0，故

点评

题中所给的角都是非特殊角，从表面上看是很难求出的，但仔细观察非特殊角与特殊角的关系，就不难发现这种解题的方法了。

题型三：给值求角

例6已知且，则β=____。

解：由，可得因为所以sin（α-β）=

由上可得cosβ=cos[α-（α-β）]=

点评

解答本题的关键在于角的变换，即β=α-（α-β）。

例7已知α，β∈（0，π），且tan（α-β）=，则2α-β的值为____。

解：由α=（α-β）+β，可得tanα=可知

给值求角时，应先求出角的某个三角函数值，再求出角的取值范围，最后确定角的大小。

感悟与提高

求（1+tan1°）（1+tan2°）·…·（1+tan 43°）（1+tan 44°）的值。

提示：由所给角度成等差数列，可进行整体处理。设S=（1+tan 1°）（1+tan 2°）·…·（1+tan 43°）（1+tan 44°），则S=（1+tan 44°）（1+tan 43°）·…·（1+tan 2°）（1+tan 1°）。

上述两式相乘可得S2=[（1+tan 1°）（1+tan 44°）]·[（1+tan 2°）·（1+tan 43°）]·…·[（1+tan 44°）（1+tan 1°）]。

当α+β=45°时，tan（α+β）=，所以tanα+tanβ+tanα·tanβ=1，即（1+tanα）（1+tanβ）=2。

于是可得S2=244，即S=222。

所以原式=222。