扫描三角恒等变换中的解题误区

■谢邦城

三角恒等变换的方法灵活多变，突出对思维的灵活性和严密性的考查。同学们在解题时，稍有不慎，便会出现增解、漏解或错解的情况。下面归纳三角恒等变换求解中的误区，希望能给同学们以警示。

误区1：对三角函数的定义理解出错

例1已知角θ的终边落在直线y=-3x上，求2 sinθ+3 cosθ的值。

错解：取该直线上一点（1，-3），则sinθ=-3，cosθ=1，所以2 sinθ+3 sinθ=2×（-3）+3×1=-3。

剖析：上述解法对sinθ=y，cosθ=x的理解有误，定义中的点（x，y）应是角θ终边与单位圆的交点坐标，而不是任意点。设角θ终边与单位圆的交点为（x，y），则解得

警示：这类问题需要借助单位圆，将角θ终边上的点转化成终边与单位圆的交点，再依据三角函数的定义求解。

纠错练习1：若α的终边所在直线经过点则sinα=____。

提示：由点P的坐标可知直线过第二、四象限。若α的终边在第二象限，则sinα=；若α的终边在第四象限，则sinα

误区2：忽视轴线角的讨论

例2已知sinα=2 sinβ，tanα=3 tanβ，求cosα的值。

错解：因为，所以

由sin2β+cos2β=1，可得cos2α=1，解得，即

剖析：上述解法是在tanα≠0，tanβ≠0的前提下得到的结果，而已知条件包含了tanα=0，tanβ=0的情形，即轴线角α=β=kπ（k∈Z），此时cosα=±1也满足题意。

警示：在三角函数求值中，熟练选用三角公式和正确把握各个公式成立的前提条件是解题的关键。解答本题要注意对轴线角的讨论，以避免漏解。

纠错练习2：已知α为第三象限角，则2α终边落在____。

提示：由α是第三象限角，可得2kπ+π，则4kπ+2 π＜2α＜4kπ+3 π，k∈Z，故2α的终边落在第一、二象限或y轴的非负半轴上。

误区3：忽视三角函数求值中的隐含条件

例3若α，β，γ均为锐角，且sinα+sinγ=sinβ，cosβ+cosγ=cosα，则α-β等于（ ）。

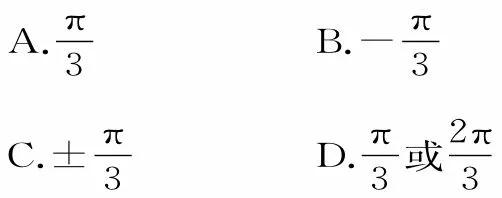
错解：由已知条件可得sinα-sinβ=-sinγ，cosα-cosβ=cosγ，两式平方相加可得因为α，β均为锐角，所以，故应选C。

剖析：上述解法没有充分利用α，β，γ均为锐角的条件导致增解。

由已知条件可得sinα-sinβ=-sinγ，cosα-cosβ=cosγ，两式平方相加可得由于γ为锐角，可知sinαsinβ=-sinγ＜0，所以sinα＜sinβ。

又α，β均为锐角，可得α＜β，故-β＜0，可知应选B。

警示：由α，β，γ均为锐角，可得隐含条件sinα＜sinβ，即α＜β，这也是解答本题的关键。

纠错练习3：设方程的两根为x1，x2，记x1=tanα，x2=tanβ，0＜，则α+β=____。

提示：由方程的判别式恒大于0，且可知x1＜0，x2＜0。

因为x1=tanα，x2=tanβ，所以α，β∈可得

又-π＜α+β＜0，故

误区4：给值求角中选用三角函数名称不当

例4若，且α，β均为锐角，求2α+2β的值。

错解：因为α为锐角，所以cosα=

因为β为锐角，所以

又因为sin（α+β）=sinαcosβ+cosα·，且＜π，所以或，即2α+2β或

剖析：因为函数y=sinx在[0，π]上不是单调函数，y=cosx在[0，π]上是单调函数，所以应求cos（α+β）的值，以防止增解。

由上面解法可得cos（α+β）=cosαcosβ

警示：由三角函数的值确定角的大小，一定要结合角的范围选择合适的三角函数。一般地，已知正切函数值，选正切函数；已知正、余弦函数值，若角在（0，π）上，选余弦函数，若角在上，选正弦函数。

纠错练习4：若A，B均为锐角，且tanA则A+2B的值为（ ）。

提示：由且B为锐角，可得，即得tanB=，所以

误区5：忽视三角函数值对角的影响

例5已知且α∈（0，π），β∈（0，π），求2α-β的值。

错解：由可得 tanα=tan[（α-β）+β]=所 以 tan 2α=则 tan （2α-β）=

由α∈（0，π），β∈（0，π）可得2α-β∈（-π，2 π）。

剖析：上述解法在求2α-β的范围时，只是依据了题目所给的α∈（0，π）和β∈（0，π），而忽视了三角函数值对其角的取值范围的限制。

又因为tan（2α-β）=1，所以

警示：给值求角时，角的取值范围容易被忽视而出现增解，因此要注意三角函数值对角的取值范围的限制。

纠错练习5：已知0＜θ＜π，sinθ+cosθ则cos 2θ=____。

提示：因为0＜θ＜π，sinθ+cosθ=＜0，所以对两边平方可得，所以π＜2θ＜

感悟与提高

参考答案：

1.提 示：因 为所 以

2.提示：原式