例谈数学规范答题*—基于“由-得-即-则-故”解答模式研究的思考

甘肃省金塔县中学(735300)闫飞

甘肃省金塔县解放路小学(735300) 闫玉梅

从小学，初中，高中数学教学的过程来看，困扰数学教师教学效果的原因可能很多，而上课学生听得懂，但不能有条理的规范书写是目前数学教学中存在的普遍问题，也是数学教师最烦心的事.规范的作业、试卷大多数是少数学习成绩好的学生，而多数学习成绩一般的学生存在最大的问题就是不能规范书写，这部分学生的作业往往是字迹潦草无法辨认，写出来的内容条理混乱，条件和结论倒置，要不就是写了一大堆，拖泥带水、主次不分，没有突出重点.“有因无果”，“有因错果”，“无因有果”的现象是作业，试卷中存在的普遍问题.怎么解决上课听得懂，课后不会做的顽疾呢? 针对该问题， 我于2017年主持了省级课题《网络背景下高中数学规范解答模式的对比与研究》，我们课题组成员通过“因为-所以”，“推出(⇒)”，“由-得-即-则-故”三种模式分析与对比，应用与实践，发现“由-得-即-则-故”模式的书写不仅适合所有的题型，而且它的书写模式学生更易于接受，学生应用“由-得-即-则-故”模式，作业、试卷的效果有了很大的改善，教学效果，教学成绩也有了显著的提升.为了能提升我们广大数学教师课堂教学的效果，特将我们对“由-得-即-则-故”模式的研究与思考分享给大家，愿学生规范的书写能给我们数学教学生活带来美的享受和成功的喜悦.

一、“由-得-即-则-故”模式的介绍

“由”就是找切入题的“切点”，也就是找与问题有关的原因如：已知条件，定理，题设条件等.

“得”就是由已知条件，定理，题设条件等能得到与解决问题有关的结论，结果，式子等.

“即”就是对结果，结论，式子等或进一步化简，或转化，或等价，沿着问题“出口”走.

“则”就是即的前提下得到的结论，结果，式子等.

“故”就是对问题最后结论的总结与回答.

二、“由-得-即-则-故”模式的应用与举例

解由α 为锐角得而即

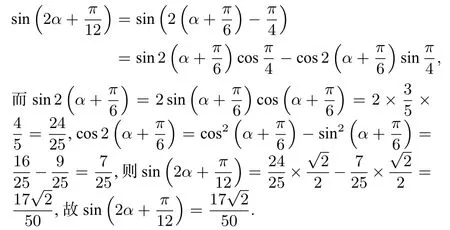
分析该例是高中数学代数板块中一道三角函数例题，用“由-得-(而)-即-(而)-则-故”模式将该题的解答过程合理的串连了起来，仿佛是从前到后向学生描述一则故事，尤其是“得”后面“而”的应用使作者非常自然引入了一个重要条件(或原因)为下一步“即”补充完整了原因，“即”后面的“而”应用同样又给下一步的“则”补充完整了原因，使得该题的解答过程环环相扣，读完给人一种赏心悦目的感觉，数学语言应用简洁明了， 这样的书写更贴近我们学生的实际，符合他们思考方式和表述方式.

(几何应用) 例2 如图， 三棱锥A -BCD 被一平面所截， 截面为平行四边形EFGH.求证：CD//平面EFGH.

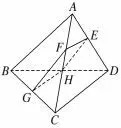
图1

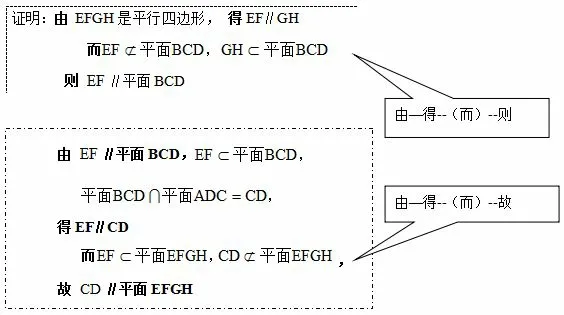
分析该例是高中数学几何板块中一道立体几何例题，用“由-得-即-则-故”模式将该问题的关键两部显示的很有层次感，真正体现了解决数学问题最为关键的问题：条理性.第一步，“由-得-(而)-则”得到的结论无需化简， 所以少了“即”，“而”的作用是补充条件与得的结论作为新的条件走向了下一步“则”.第二步，“由-得-(而)-故”由三个条件(原因)得到一个结论，“而”又补充两个条件(原因)得结论，由于解题结束了就跳过则用“故”回答.由此可见，“由-得-即-则-故”模式将繁杂的立体几何证明题中定理反映的如此明晰是其他解答模式所不能及的，另外，从“由-得-即-则-故”模式的书写中又能清楚反映学生对定义，定理的理解程度，便于教师掌握学情.

三、“由-得-即-则-故”模式的应用与思考

首先“由-得-即-则-故”解答模式注重“由因导果”过程，是演绎推理最直接的反映方式.用“由-得-即-则-故”解答模式可以使得数学语言应用简洁明了， 解答过程环环相扣，也可以使每一层(每一个问题)自然形成一个独立的小环节，也可以使层与层之间形成嵌套， 不管是简单还是复杂问题，或者不同的数学证明方法(如综合法，分析法，反证法，数学归纳法等)都能用“由-得-即-则-故”解答模式解决.其次“由-得-即-则-故”解答模式也可根据题设适时引进“设”，“假设”，“令”，“当”，“若”，“而”“且”等连接词，使我们的规范书写能灵活应对不同的题型，不同的题设条件，进而使得的解答过程环环相扣，书写(说理)具有条理性，前后语言具有连贯性、文学味，读完给人一种赏心悦目的感觉，结构框架清晰明了.总之、“由-得-即-则-故”解答模式下每一道数学解答题的规范书写就好像是一副精美的书法作品，每个字的摆布都有他特定位置，每一个字的使用都有他独特“用意”，又好像规范分类的书架，层次分明;又宛如是给大家讲述一个优美的故事情节，引导读者从头读到尾.这样的书写模式更贴近我们的学生的实际，符合他们思考方式和表述方式.

规范的书写是对所学知识点理解程度的一种最直接的反映，也是对所学知识不足方面的一种有力补充的方式.一个清晰的规范解题过程是学生逻辑思维的独白，也可展示一名学生数学知识的底蕴.探索引导学生规范的解答模式是提升教学效果有效方式，经过应用与实践，“由-得-即-则-故”解答模式是一个值得大家借鉴一种数学规范解答模式.