以中学数学问题辅助高等数学教学*

任翠环 周 旭

(华北理工大学，河北 唐山 063210)

历经高考洗礼刚刚迈入大学的学子，在高中模块化教学基础上，学过的知识不成系统，往往领会不到高等数学知识对中学知识的指导作用[1]，认为高等数学知识晦涩难懂，从而缺乏学习高等数学的兴趣，使高等数学的挂科率居高不下。为了改变这种现状，有必要引导学生从一些具体实例中，让学生认识到高等数学知识丰富中学的数学理论，提供更简便的数学方法，拓展解题思路，从而调动学生学习高数的积极性，提高教学效果。

一、高等数学对中学的一些结论进行严格的推导，提供了理论依据

取圆锥体顶点O为坐标原点，过顶点垂直于底面的直线为x轴，过坐标原点与x轴垂直的直线为y轴，如下图所示：

这个例子可以看出初等数学是高等数学的基础，高等数学为初等数学提供理论依据。

二、高等数学为证明不等式提供了新方法，简化计算

在中学中，函数是必修内容，通常考察不等式的证明。如：

本题用中学数学的方法，求解过程比较繁琐，具体证明过程如下：

此题若用高等数学当中的导数求解，只需证明所给函数是凹函数，证明过程大大简化。

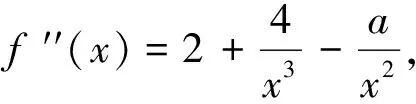
从这个例子可知，高等数学的知识不仅可以解决新问题，还可简化中学数学问题。将初等数学和高等数学结合起来，有利于巩固旧知识，学习新知识，拓展解题思路。

三、结束语

高等数学和中学数学有着千丝万缕的联系，在高等数学的教学中，联系旧知识，讲授新知识，将高等数学和初等数学有机结合起来，引导学生领会数学知识间内在本质的联系，才能使学生形成完整的认知结构，从而提高学生分析问题和解决问题的能力。