高等数学课程中一阶微分方程的基本求解方法探讨*

陆心怡

(池州学院，安徽 池州 247000)

微分方程的求解问题是大学高等数学教学中的一个重点、难点.一般来说，微分方程所反应的是我们在实际问题中需要寻求的函数关系及其导数之间的关系式，那么如何去寻求未知的函数关系在现实意义中就显得尤为重要。一阶微分方程是微分方程的基础，这里就我在高等数学课堂上的一点心得体会，结合三个例子总结探讨一阶微分方程的基本求解方法。

一、可分离变量的微分方程

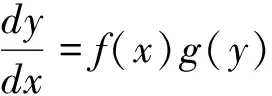
例1求微分方程sec2xtanydx+sec2ytanxdy=0的通解.

解这是一个可分离变量的微分方程，分离变量得

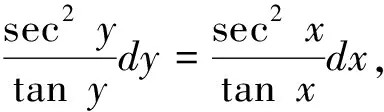
即 ln|tany|=-ln|tanx|+C1

于是得到通解为 tanx？tanyC.(C=？ec1)

二、齐次方程

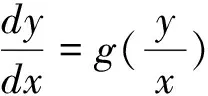
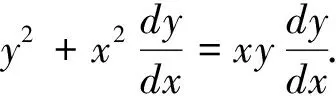
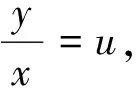
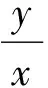
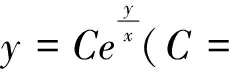
三、一阶线性微分方程

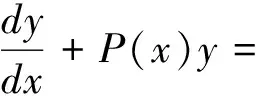
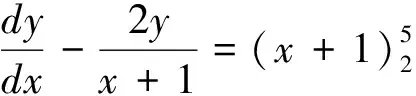
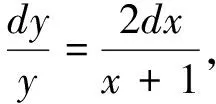
两端积分得 ln|y|=2ln|x+1|+C1,

于是通解为y=C(x+1)2.

再运用常数变易法，把C换成u=u(x)，即y=u(x+1)2,

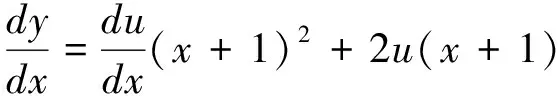
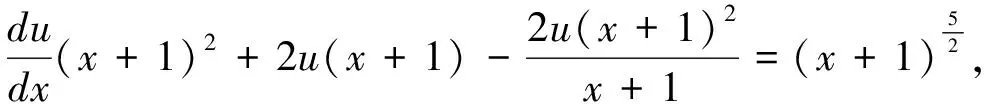
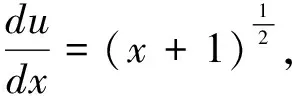
两边积分得u=

也可直接代入通解公式y=e((x)eP(x)dxdx+C).进行求解.

解法二直接代入通解公式

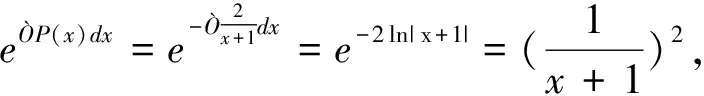
于是e=(x+1)2,

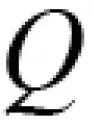
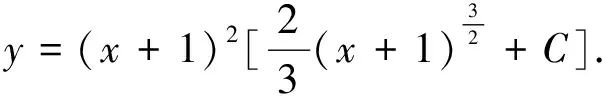
一阶微分方程是大学数学微分方程的基础部分，遇到不同的微分方程求解题目要首先辨别是哪种类型，再运用对应的合适方法进行求解。为了使得运算更为流畅和简便，也需要仔细的观察和多番的练习，这对于学好微分方程乃至高等数学都是有好处的。