基于剪切振动模态的压电复合材料应用于水声换能器的研究

贾俊博，秦 雷,3，仲 超，王丽坤,3

(1.北京信息科技大学 传感器北京市重点实验室，北京 100192；2.北京信息科技大学 光电测试技术北京市重点实验室，北京 100192；3.北京信息科技大学 教育部现代测控技术重点实验室，北京 100192)

压电复合材料作为换能器的核心敏感材料经历了近半个世纪的快速发展。因其既具有压电相材料的压电性能又可以通过添加聚合物相来提高材料的综合性能，故在超声无损探伤、地质探测、水下声呐通信等方面有着无可替代的作用[1-3]。压电陶瓷的剪切振动模态作为典型振动模态的一种，其极化方向和电场方向垂直分布，在激励作用下则在极化方向和电场方向组成的平面内产生剪切形变[4]。对于大多数压电元件，压电陶瓷剪切振动模态的压电系数d15比d33系数高出50%～70%[5-6]，且其频率常数、介电常数都较低。目前，国内外对于压电材料d15模态研究较少，大多数是通过结构设计来利用d15独特的剪切形变，且多用于能量收集领域。如美国新泽西州立大学的Safari等[7]设计了一种应用d15模式的压电复合材料，压电陶瓷柱以45°角放置于聚合物中。然而由于其工艺复杂，性能提升不明显，没能得到广泛应用。Ren等[8]将工作于d15模态的PMNPT单晶应用于俘能器上，通过质量块和悬臂梁的作用，将外界振动转化为压电单晶的切向形变，取得了较高的输出电功率。Zhao等[9]将两块工作于d15模态的PZT压电陶瓷串联应用于压电俘能器上，性能得到了进一步提高。Trindade等[10-11]应用d15模态设计了一种复合材料。该压电材料的压电应变常数d15和介电常数并没有减小，而压电电压常数e15和剪切模量却降低了90%。Yan等[12]提出基于d15剪切机电耦合的接触型行波压电微电机，采用单体PZT作为定子，定子在交变电场的作用下产生一阶和二阶的弯曲振动模态，摆动的定子表面产生行波并以顺时针或逆时针的方向摩擦转子使其转动。该结构较同类型产品优势在于小型化，转速高，扭矩大。Han等[13]应用压电陶瓷的d15模态构成压电圆管，通过剪切振动带动磁性材料旋转形成磁电耦合，较非d15模态的剪切换能器相比能量密度大幅提高，证明其在磁传感器，换能器以及俘能器等方面有较好的应用前景。Yuan等[14]提出剪切压电纤维复合材料(Shear Piezoelectric Fiber Composites,SPFC)的新颖结构，其极化方向是厚度方向，在水平方向交替施加电场。在驱动条件下，SPFC显示出较大的剪切应变。至此，越来越多的科研学者青睐于d15的优良特性。可见，d15剪切振动模态还有着极大的研究价值和广阔的应用前景。

本文提出一种基于剪切振动的新型压电复合材料。通过设计梯形过渡层，将压电陶瓷产生的剪切振动转化为过渡层的厚度振动，以此来达到应用剪切振动模态产生纵波的目的，进而使得这种复合材料可以应用于水声或超声换能器。

1 结构和工作原理

基于剪切振动的压电复合材料结构，如图1所示。该复合材料由压电陶瓷相、被动相构成。其中沿X轴正向极化的压电陶瓷以及沿X轴负向极化的压电陶瓷沿X轴方向交替排列。压电陶瓷间粘接被动相，垂直于Z轴的两个陶瓷面上制备电极。

图1 基于剪切振动的压电复合材料结构示意图Fig.1 The structure diagram of piezoelectric composite based on d15 mode

如图2所示是压电复合材料的极化方向及振动模态示意图。由于极化方向与电场方向夹角为90°，所以会激发压电陶瓷的d15振动模态。即在极化方向为P方向的压电陶瓷材料上，施加E方向(即垂直于极化方向)的电激励时，在EP组成的平面内产生切向形变。由图2可知，第一和第二个基元表示了陶瓷材料的极化方向P和电场方向E；第三、第四和第五个基元表示了陶瓷材料在电场激励下产生的形变。可以看出第三、第四两个基元共同作用可以带动基元间的被动相a(即被动相填充层)产生振动，而第四、第五个基元共同作用可以带动被动相产生相反的振动。这种振动再通过梯形被动相b(即被动相过渡层)分别传递到上下表面的被动相平面c(即被动相平面层)上，从而完成机电转换过程，实现压电陶瓷剪切振动到复合材料厚度振动的转化。

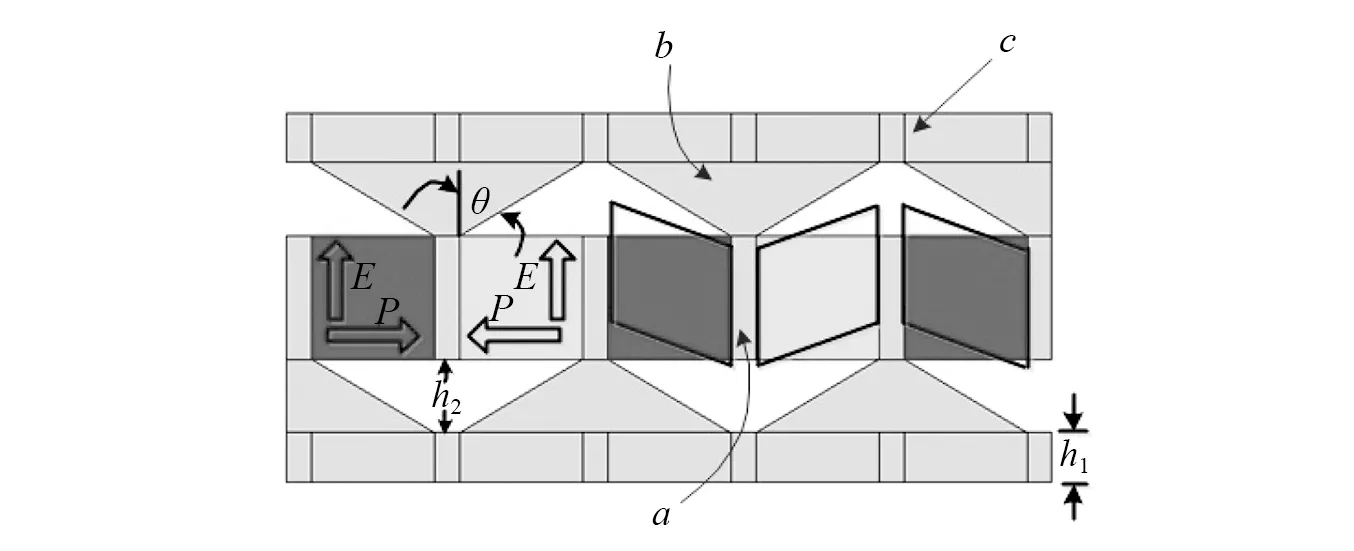
图2 基于剪切振动的压电复合材料振动原理图Fig.2 The vibration principle diagram of piezoelectric composite based on d15 mode

2 有限元参数分析

Kranz等[15]发现不同尺寸参数会对复合材料机电耦合系数产生较大影响，而机电耦合系数是表征换能器能量转换效率的重要指标。因此本文前期对尺寸参数与机电耦合系数的关系做了详细研究，发现对于PZT-5A型压电陶瓷，当电场方向尺寸与极化方向尺寸之比接近1.1时，剪切振动的机电耦合系数达到最高值0.56。为使加工方便，本文选取压电陶瓷电场方向尺寸与极化方向尺寸均为10 mm、长度为7 mm的陶瓷小块作为基元。运用商业仿真软件Ansys®(ANSYS,Inc.USA)对单一基元的陶瓷振动情况进行谐响应分析并观测其谐振处的振动情况。同时，制备相同尺寸的PZT-5A型压电陶瓷基元，去掉原有极化方向的电极并在与之垂直方向溅射电极。通过HP 4294A(Agilent Technologies Inc.USA)阻抗分析仪测量其导纳曲线，测试结果如图3所示。由图3可知，导纳曲线可以看出该尺寸下的压电陶瓷基元谐振频率仿真结果为107.19 kHz，实验测量结果为105.85 kHz，误差为1.26%。仿真和实验结果吻合较好。实测结果的谐振频率和谐振点处的电导值较仿真结果均略有下降，这是由于有限元仿真软件所用的材料参数与实际情况略有差别。

应用激光多普勒测振仪(PSV-400 Polytec Inc.Germany)观测样品的实际振动情况。如图4(a)为有限元模型及其剪切形变。图4(b)为用激光多普勒测振仪测量得到的PZT-5A压电陶瓷块的剪切振动模态。被测的振动表面是图4(a)中所示的上表面。由图4(a)可知，图中压电陶瓷上表面一部分相位为正，一部分相位为负，与图4(a)给出的剪切振动有限元分析结果较符合。本文选用工作于这种剪切振动的压电陶瓷块作为压电复合材料的振动基元。

图3 单一基元电导有限元仿真和实测结果对比Fig.3 Contrast of single-element conductance finite element simulation and measured results

图4 单一基元的有限元仿真和实测结果对比Fig.4 Comparison of a single-element finite element simulation and measured results

在这种新型压电复合材料中，本文拟采用环氧树脂以及硬铝作为过渡层材料。被动相过渡层材料很大程度上决定着剪切振动的传递效果，将被动相过渡层研究类比匹配层理论。依据声阻抗与密度、声速的关系Z=ρc，式中ρ为匹配层的密度(kg/m3)，c为声波在匹配层中的传播速度(m/s)[16]，声阻抗与材料密度成正比。为了减少声波传递过程中的能量损失，即降低声阻抗，故理论上应该选取密度低的材料作为被动相过渡层材料。材料参数如表1所示。因此本文选取密度较低，杨氏模量逐步增大的环氧树脂、硬铝两种常用的材料作为过渡层材料进行仿真分析。

环氧树脂作为过渡层材料时，复合材料的仿真电导曲线与其不同谐振频率处的振动形态如图5所示。分别观察39.8 kHz和114.6 kHz处的振动模态，由图5可知，压电陶瓷剪切形变沿X轴分量会对基元间的环氧树脂产生挤压作用，从而影响整体过渡层的振动传递效果。故本文选择杨氏模量较高，密度较小的硬铝材料代替过渡层材料进行进一步仿真分析。

表1 不同过渡层材料参数表Tab.1 The material parameters of different transitional layer

硬铝过渡层材料的仿真电导曲线与其不同谐振频率处的振动形态，如图6所示。由图6可知，相比图5低频率处的谐振峰得到了加强。我们分别选取27.91 kHz，69.77 kHz，147.51 kHz三处的振动情况进行观察，可以看出低频段处的振动形态较为理想，满足了将剪切振动转化为被动相平面层的振动。但是也可以看出辐射面上的振动相位并不一致，这会影响声辐射性能，因此其结构仍需改进。

3 实验验证结果

依据仿真分析的参数结果，通过精密机械加工与粘接的方法制备了最优参数下的实物振子。运用激光多普勒振动分析仪观察被动相平面层表面的振动情况，验证仿真分析的有效性以及该结构振子的可行性。为验证仿真结果分别选用环氧树脂、硬铝作为过渡层材料制成该复合材料振子，被动相平面层厚度为h1=4 mm，被动相填充层厚度h2=9 mm，被动相过渡层角度为30°。使用精密阻抗分析仪及多普勒激光测振仪测量其电导曲线与复合材料表面振动形态。

图5 环氧树脂复合材料过渡层仿真结果Fig.5 The simulation results of epoxy composite transition layer

如图7(a)所示，选用环氧树脂作为复合材料被动相时，在低频范围处复合材料表面振动起伏不一致，无法完全将剪切振动转化为厚度振动。这与仿真结果吻合。观察图7(b)选用硬铝作为复合材料被动相时，在低频范围处复合材料表面形成类似于弯张的振动模态，这是由于在此频率下剪切振动的压电陶瓷激励了硬铝的弯张振动模态。

图6 硬铝复合材料过渡层仿真结果Fig.6 The simulation results of ductile aluminum transition layer

图7 环氧树脂、硬铝复合材料过渡层实物图与激光测振对比结果Fig.7 The actual transition layer and laser vibration test results

4 简化结构模型

上述研究中发现该复合材料结构在低频时表面振动更适合辐射声波，而被动相过渡层材料是影响工作频率最主要的因素。其主要原因是压电陶瓷剪切形变会对基元间的被动相填充层产生挤压作用，基元间过渡层材料杨氏模量越高，越易在低频段处产生较高的谐振峰。故我们简化了复合材料结构，将压电陶瓷沿X轴直接交替粘接，在接缝处直接粘接梯形辐射面。如图8(a)所示，陶瓷基元直接粘接相连。通过激光测振仪观察表面振动模态，可以看到分别在33 kHz，57 kHz和95 kHz附近出现谐振，其中57 kHz附近振速最大，其振动表面出现典型的剪切振动模态。图8(b)所示，将梯形辐射面直接粘接在陶瓷块接缝处，可以看到粘接辐射面后，振子谐振峰偏移至28 kHz，60 kHz和86 kHz附近。观察辐射上表面振动情况，辐射面出现整体的起伏，达到了将剪切振动转化为辐射面厚度的振动的目的。

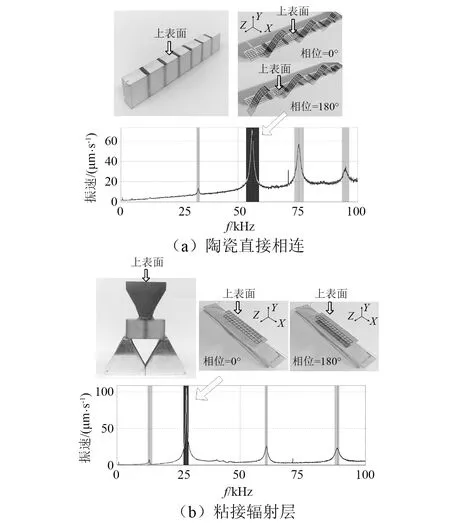
图8 简化结构复合材料过渡层实物图与激光测振结果Fig.8 The simplified structure of the composite material transition layer and laser vibration measurement results

将简化结构的复合材料振子依图9所示制作换能器。由图9可知，振子厚度为35 mm，振子的辐射面长度为15 mm，每个振子厚度为5 mm，本试验由三组振子并联而成，故换能器的辐射面积为15 mm×5 mm×3。

图9 简化结构复合材料换能器结构示意图Fig.9 Simplified structure of the composite material transducer

本文研制的换能器在中船重工集团公司长城无线电厂的水池中进行了水下发射性能测试。结果如图10所示。换能器分别在28 kHz，55 kHz和86 kHz处产生120.1 dB，119.1 dB和127.6 dB三个发射电压响应的波峰，与图8(b)激光测振峰值的频率较为吻合。其中28 kHz与55 kHz处的两个谐振产生了较强的耦合，在24～60 kHz内其发射电压响应起伏小于6 dB。而发射电压和电流响应曲线在63 kHz附近产生了一个较大的凹陷，无法与86 kHz处的谐振耦合，进一步拓展带宽。虽然目前换能器的发射电压响应较低，但是其发射电流响应达到174.8 dB，这是因为当前换能器体积过小，压电陶瓷的阻抗较大造成的。因此换能器需要施加较高电压才能驱动。

图10 换能器水下发射电压、电流响应测试结果Fig.10 The measured emission voltage,current response of transducer

表2给出了本文研制换能器发射性能与丹麦Reson公司出产的TC2084型高功率宽带换能器的性能对比。通过对比可知，TC2084型换能器谐振频率为33 kHz，发射电压响应为166 dB，-3 dB指向性开角为20°，根据活塞辐射的指向性公式可知粗略计算其辐射面半径为130 mm。若将本文的换能器发射响应折算成等面积的情况，则发射电压响应应该增加38.9 dB，达到159 dB。相应的声源级在405 V电压驱动时将可达到210 dB。再考虑辐射面积增加后所获得的指向性增益，则发射响应会进一步提高。

表2 水声换能器发射性能对比Tab.2 The comparison of underwater transducer launch performance

5 结 论

通过巧妙设计被动相过渡层结构，我们将压电陶瓷的剪切振动形式成果转化为被动相表面的厚度振动。研究发现，该结构在整体厚度为47.7 mm的情况下产生了约28 kHz的谐振，相比于应用d33模态的压电复合材料，其频率常数较低，可以用较小的结构产生低频振动。通过有限元分析软件得出，当使用如硬铝等杨氏模量较高的材料作为过渡层材料时，剪切振动与厚度振动间的传递效果更好。对设计结构进行进一步简化，将工作于d15模态的压电陶瓷沿极化方向交替粘接，在接缝处直接连接被动相过渡辐射层。实验研究表明简化结构同样达到将剪切振动转化为辐射面厚度振动的目的。最后我们将简化结构制作水下换能器，测试结果表明在辐射面积为15 mm×40 mm时，在24～60 kHz平均发射电压响应可以达到120 dB。且可通过继续增加振子数量，增大辐射面积从而有效提高发射电压响应及声源级。该类型换能器的研发为低频小尺寸发射换能器提供了新思路。