有级转向履带车辆的驾驶员操控行为模型

2020-02-06王博洋龚建伟熊光明张瑞增陈慧岩席军强

兵工学报 2020年12期

王博洋，龚建伟，熊光明，张瑞增，陈慧岩，席军强

(北京理工大学机械与车辆学院，北京 100081)

0 引言

基于离合器转向机或二级行星转向机的有级转向履带车辆，由于转向机结构简单、成本低廉、使用维护方便等优势[1]，不仅仍然大量装备于部队，并且经由电控化和无人化改造后，在众多方面存在潜在的运用价值[2-4]。但无论是基于离合器转向机还是二级行星转向机的有级转向履带车辆，在转向过程中都只存在极其有限的规定转向半径，如何表征非规定转向半径的转向模式，并探究不同转向模式之间的切换规律，继而根据驾驶环境实现转向操控量的预测，是有级转向履带车辆无人化改造过程中性能提升的关键。

示教学习是一种典型的人类操控行为学习方法，该学习方法不仅能够从人类示范数据中提取操作技巧，并且能够将所学习得到的操控经验泛化再利用到新的场景之中[5-7]。图论是描述离散操控基元切换的常用方法。Kulic等以人类示范动作数据集为依托，对描述类人机器人全身运动的基元进行了提取并完成了切换规则的表征，所提取出的基元序列切换图被成功用于类人机器人的控制领域[8]；Manschitz等以人工引导的机械臂示范动作数据集为依托，对机械臂的操控基元序列进行了表征，并给出了基于状态触发的切换规则，实现了对机械臂抓取任务的描述[9]。虽然上述示教学习算法都借助于人工示教数据实现了运动基元以及基元序列切换关系的表征和泛化利用，但其所使用的人工示教数据都是小范围空间内的独立关节运动数据，采集实验也为同场景下的多次重复数据采集。然而，驾驶行为的数据采集实验往往面向一般的驾驶场景，场景重复度较低，采集得到的轨迹与操控表征参量也与关节运动数据存在差异。

对驾驶员行为的研究能够有效提升无人车以及辅助驾驶技术的智能化水平[10-11]，将复杂的驾驶任务分解成基本的基元能够提升驾驶员行为预测的精度[12-14]。Yi等通过构建车辆轨迹类别与操控行为的对应关系，有效提升了对于驾驶员操控行为的预测精度[12]；Taniguchi等也通过将复杂驾驶行为表征成离散基元操控序列的形式，实现了对于驾驶员离散操控行为与连续操控量的准确预测[13]。但上述研究只针对轮式阿克曼转向车辆，与履带车在结构上以及转向操控特性上存在显著差异[1]，如何根据有级转向车辆的结构特点提出轨迹层与操控层的关联关系，并在此基础上完成驾驶行为的预测，是需要解决的问题。

前期的研究工作已经针对基于离合器转向机的有级转向履带车辆完成了横向控制驾驶员模型构建工作，并实现了对于离散转向模式的预测[2]。本文以驾驶员操控经验数据为依托，从驾驶员操控行为模型构建的角度开展研究。通过对操控基元序列的提取与类别辨识，构建轨迹层与操控行为层的关联关系，利用每一个轨迹类别下单独训练的隐马尔可夫- 高斯混合模型(HMM-GMM)生成具有不确定性表征的转向操控量预测结果，并从操控基元序列表征与类别辨识的角度，对比基于离合器转向机和二级行星转向机两种典型有级转向履带车辆的转向特性。整体的处理流程如图1所示。图1中M1、M2、M3为操控基元。

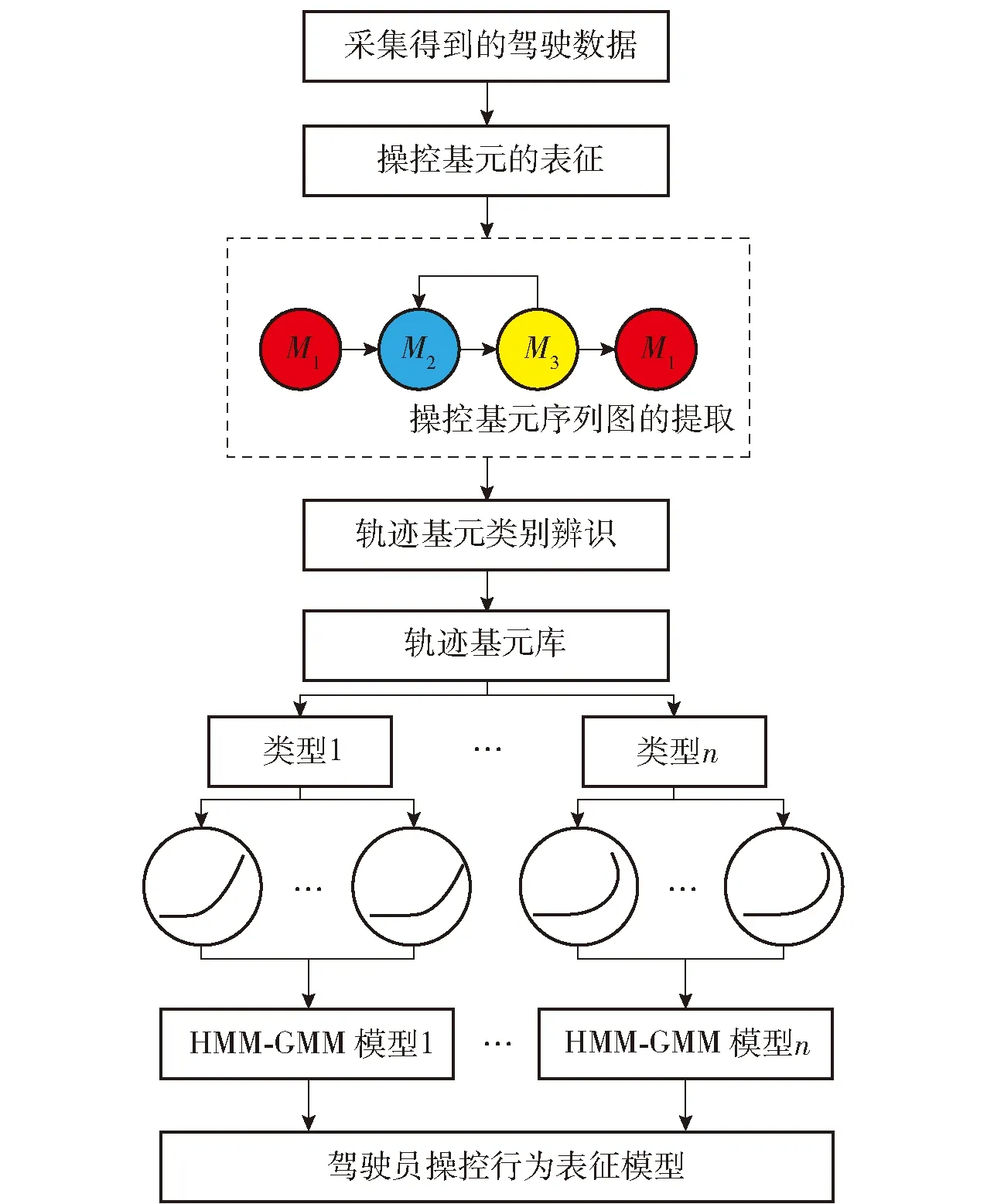
图1 有级转向履带车辆驾驶员操控行为模型训练流程Fig.1 Training process of stepped steering tracked vehicle driver control model

1 问题陈述

根据采集得到的车辆轨迹观测数据O与驾驶员转向操控量数据S，本文的目的是通过有向图H的形式构建操控基元时序切换序列，实现对复杂驾驶任务的简化分解，并建立轨迹观测数据O与转向操控量数据S之间的映射关系，完成对于转向操控量的预测。

本文使用的主要参量定义说明如下：

1)O(t)是车辆实际轨迹的观测数据，O(t)=[Δθ(t),v(t)]T∈R2×1，其中Δθ(t)与v(t)分别是航向变化偏差时序点与车辆行驶速度时序点。

2)S(t)是驾驶员转向操控量观测数据，S(t)=[sl(t),sr(t)]T∈R2×1，其中sl(t)与sr(t)分别为左、右两侧的转向操纵控制量时序点。

3)H是描述操控基元序列的有向图表征方式，H=(V(H),Eφ(H))，其中：V(H)={x1,…,xj}为有向图的节点集，也是该操控序列中各操控基元的聚类编号集；Eφ(H)={a1,…,aj}为有向图中的有序对，记录了操控序列中各操控基元的切换关系，φ(a1)=(x1,x2)是其中一个有序对的具体表述。

本文提出的方法致力于解决如下两个核心问题：1)如何从驾驶转向操控数据S中提取出相应的操控基元序列，构建各挡位下的操控基元序列切换图H，并以此为依据实现从连续轨迹数据O中对轨迹基元的提取与类别划分；2)如何利用轨迹层与操控层的关联关系构建双层驾驶员模型，在给定期望轨迹的前提下，提升对驾驶员操控行为的预测精度。

2 操控基元序列提取与再生成

2.1 基于高斯混合模型(GMM)的操控基元聚类

基于离合器转向机或二级行星转向机的有级转向履带车辆能够依据转向机的结构特点，将转向过程划分成若干离散的转向模式，但上述离散的转向模式并未涉及到转向机中的摩擦元件处于滑磨状态下所产生的转向运动。为了更全面地表征有级转向履带车辆的转向模式，本文以驾驶员的真实驾驶数据为依托，在保留直驶与原地转向两种特殊转向模式基础上，利用GMM模型对行进间转向过程中左右两侧的操纵控制量进行聚类分析，提取出相应的操控基元，以求能够达到对行进间转向模式进行细致划分的目的。

表征操控基元的高斯混合模型如(1)式和(2)式所示：

(1)

(2)

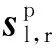
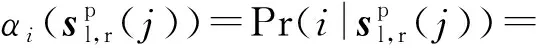
(3)

式中：j为两侧操纵杆位置量的序号，j=1,2,…,N.

(4)

在整合直驶和原地转向这两类特殊的转向模式后，有级转向履带车辆操控基元序列D如(5)式所示：

D={Ll,Lr}.

(5)

2.2 基于有向图的操控基元序列表征与类别辨识

操控基元序列的表征以有向图的形式完成，其中有向图中的节点xi代表基元序列D中的一个特定类别的操控基元，节点xk到xl(k,l∈i)的切换关系由有序对φk,l表征。假定表征一组观测序列的有向图有m个节点，则以维度是m×m的转移数组Φ来表征节点之间的切换关系，由于在单一操控基元处始终会存在停留，转移矩阵中的φk,k是始终存在的。

通过对所观测得到的左右两侧操纵控制量时序数据S进行GMM聚类，便能够得到操控基元序列D，即生成能够描述转向观测序列的有向无环图。操控基元序列提取便是从同一挡位下的多组观测序列中，提炼出一种能够表征驾驶员操控规则的有向图表征方式。

在基于有向图表征操控基元序列的过程中，存在两种非常典型的转向观测序列整合方式，其中：局部序列图假定操控基元之间的切换是随意进行的，该序列图的节点数与操控基元的种类数完全一致，如图2所示；全局序列图则对操控基元之间的切换顺序做了更为细致的建模描述，在全局序列图中类别相同的操控基元会出现多次，如图3所示。

图2 局部序列图Fig.2 Local sequence graph

图3 全局序列图Fig.3 Global sequence graph

相比于局部序列图，全局序列图能对转向操控基元之间的切换关系进行更为细致的描述，使得驾驶员的操控规律表征更为明了，不仅明确区分了转向执行和转向回位的过程，还突出了转向过程中模式间的重复切换问题。因此，本文选用全局序列图对转向操控基元序列进行表征。

在得到各挡位下每一组驾驶数据的操控基元序列D之后，还需要进行如下两步才能完成各挡位下基于有向图表征的操控基元序列图：

1)在对每一组示范驾驶数据进行完整转向片段分割的基础上，辨识并剔除单一片段中重复的操控基元序列组合，并进行相应的合并工作。

2)在对描述单一转向片段的基元序列图进行提取的前提下，完成同一挡位下不同组操控基元序列图的合并，生成最终的全局序列图。

第1步的具体算法流程如图4所示，以操控基元序列D为输入，首先完成序列中相邻且相同的操控基元时序节点合并；其次对节点中的直驶基元进行辨识，并以此为依据实现对完整转向驾驶片段的分割提取；随后，对每一个完整转向驾驶片段中的重复切换基元对进行辨识并完成相应的剔除工作，在重新整定基元序列切换关系后，最终完成针对单一驾驶片段序列图HA的创建工作。

图4 单一基元序列图生成算法流程Fig.4 Flow chart of ingle primitive sequence graph generation algorithm

为了最终实现各挡位下全局序列图的创建，需要对各独立的转向片段基元序列图进行整合，图5描述了两个单一基元序列图(HA和HB)的合并过程。首先对输入的两个独立基元序列图进行从左到右的逐一节点比对，如果完全相同则依次合并，一旦不同则在全局序列图上直接添加基元序列切换分支，分支上所有的节点不再参与比对。依据上述方法对同一挡位下的所有单一基元序列图进行合并后，便能够得到该挡位下最终的全局操控基元序列图H.

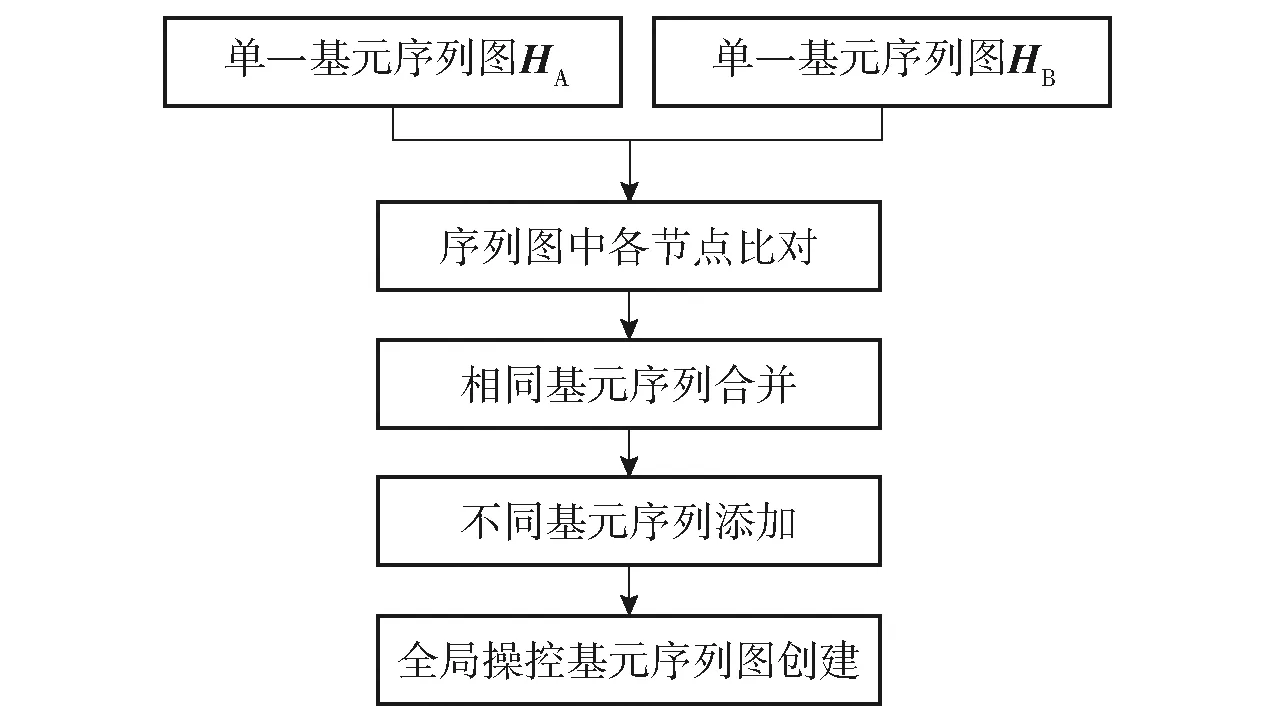
图5 全局操控基元序列图生成Fig.5 Generation of global control primitive sequence graph

各挡位下的全局操控基元序列图(见图5)完整描述了该挡位下所有可能出现的转向过程，操控基元序列类别的辨识正是基于上述全局序列图中的特征参量。具体的类别辨识分为如下两个步骤：首先，将具有相同序列图转移数组Φ的转向过程划分为同一个大类别；其次，提取序列图中各节点的停留时间ti以及重复切换节点之间的切换次数nj组成特征参量数组ψ，最终利用GMM聚类算法得到更为细致的类别划分。

ψ=[t1,…,ti,…,tI,n1,…,nj,…,nJ]，

(6)

式中：I和J的具体数值根据操控基元序列图的具体结构设定。

由于每一个操控基元序列都对应于一个完整的转向分割段，利用操控基元序列与轨迹分割段的简单映射关系，便能够实现对轨迹基元的提取以及相应的类别属性辨识，继而构建针对每一个挡位的轨迹基元库。

2.3 基于HMM-GMM的驾驶员操控行为表征

驾驶员操控行为模型由HMM-GMM模型表征，其中HMM模型由一个五元组λ定义：

λ=(D,O,π,A,B)，

(7)

式中：π为初始状态概率矩阵；A为状态转移矩阵，描述了给定观测序列O的前提下，D中各转向操控状态参量之间的转移概率值，根据A生成的转向操控区间概率密度是进行驾驶员转向操控量预测的基础；B为混淆矩阵，表征了各转向操控基元实际产生的转向效果在航向偏差变化Δθ(t)与速度v(t)层面上的统计学规律。

相比于之前的研究工作[2]只针对每一个挡位下的所有驾驶情况训练一个HMM-GMM模型，本文利用轨迹基元库中的类别属性信息(见图1)，该类别属性信息由操控基元序列的特征参量数组ψ的GMM聚类结果最终给定。在对数据进行重分组后，针对每一种类别的轨迹基元重新训练相应的HMM-GMM模型。基于HMM-GMM模型的转向操控量预测流程如图6所示。

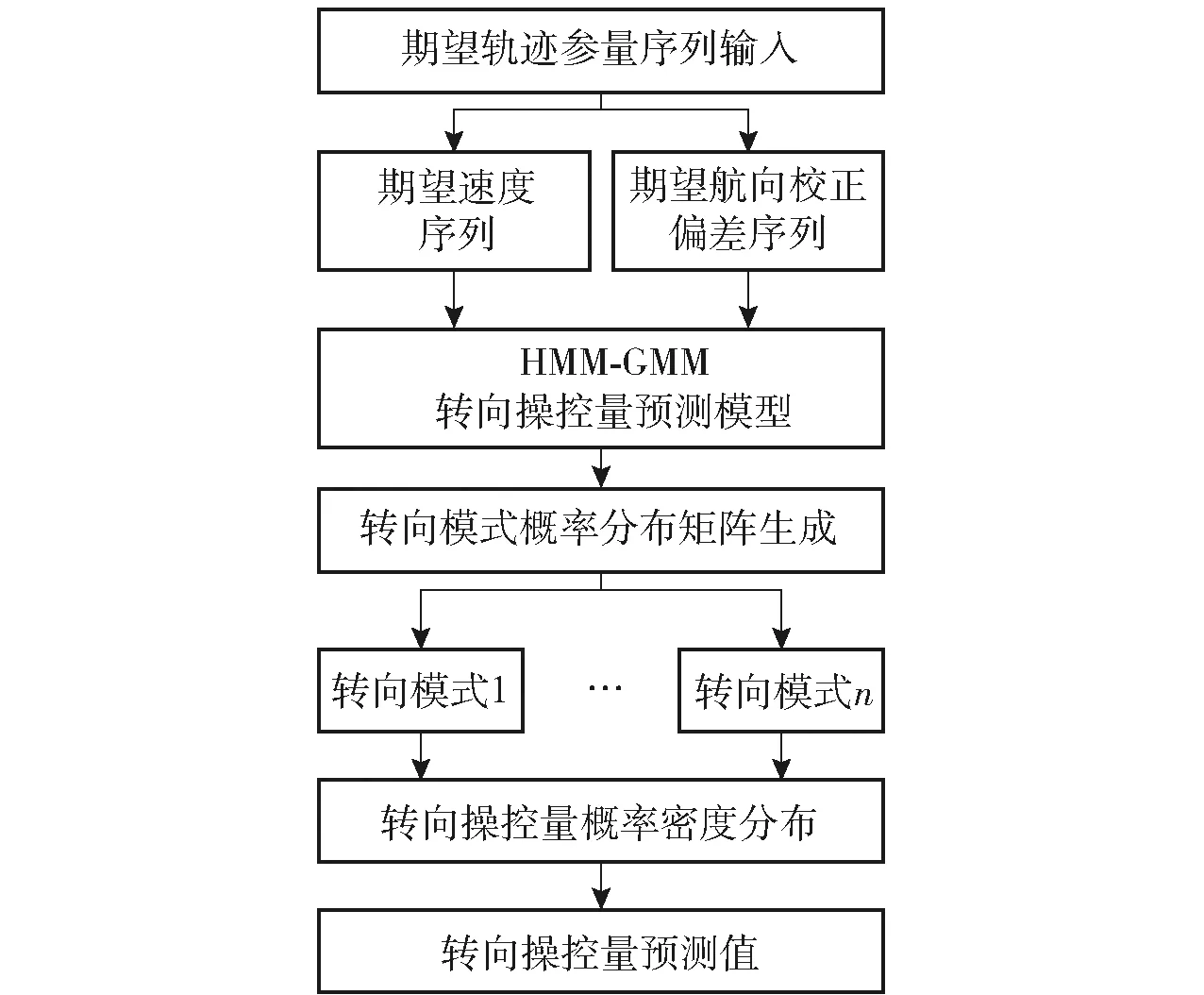
图6 基于HMM-GMM模型的转向操控量预测Fig.6 Prediction of steering control value based on HMM-GMM

以包含期望速度与期望航向校正偏差的期望轨迹参量序列作为HMM模型的观测序列输入驾驶员模型，得到每一个基于GMM聚类的操控基元与当前观测量对应的概率值αi(Ot)，

(8)

式中：Di为隐含参量第i个操控基元；Ot为t时刻的观测量。

在得到各操控基元与当前观测量对应的概率值αi(Ot)后，便能够基于所生成的转向模式概率分布矩阵，调整基于高斯模型表征的各转向操控基元权重系数，继而实现转向操控量预测值概率密度G的实时更新。

(9)

以左侧转向操控量为例，在得到t时刻实时更新的概率密度函数f(sl)后，便能够分别通过(10)式～(12)式得到转向操控量的预测值l、预测值偏差下限和上限的概率值函数F如下：

F(l)=f(sl)dsl=0.5,

(10)

(11)

(12)

3 实验结果与讨论

3.1 驾驶员行为数据采集平台及所构建的数据库

有级转向履带车辆的驾驶员行为数据采集实验由图7和图8所示基于离合器转向机或基于二级行星转向机的有级转向履带车辆共同完成。上述两个平台搭载完全相同的数据采集设备，包括OxTS公司生产的Inertial+全球卫星导航系统与惯性导航系统(GNSS/INS)组合导航系统，采集车辆底层CAN数据的数据采集单元CANoe，以及两台研华公司生产的ARK-3520P-U8A1E工控计算机。所采集到的数据都标注有系统统一提供的时间戳信息，便于后续的数据同步处理。图7和图8中Tl和Tr分别为左右侧制动器，Ll和Lr分别为左右侧转向离合器，Zl和Zr分别为左右侧转向制动器。

图7 基于离合器转向机的有级转向履带车辆Fig.7 Stepped steering tracked vehicle based on clutch steering

图8 基于二级行星转向机的有级转向履带车辆Fig.8 Stepped steering tracked vehicle based on two-stage planetary steering

整个数据采集实验只针对硬质土路面展开，采集得到的数据集涵盖了1～4挡各行驶速度下多种操控基元序列组合而成的典型场景，包括直角弯、双移线、定半径转向等场景，最终的实验场景则是多种典型场景的组合。由于本文的研究目标仅针对单一驾驶员的操控行为进行分析，而非多个驾驶员之间不同驾驶风格的辨识和表征，因此只从两个车辆平台的实验数据中挑选出单一驾驶员各6 h的全工况驾驶数据作为后续建模分析的基本数据，前期的数据采集以及后续模型的训练过程并未针对不同的单一驾驶员做区分或筛选。

车辆实际轨迹观测数据O中的航向角偏差Δθ由组合导航系统采集的航向角计算得到，车辆的行驶速度v和左右两侧的转向操控量sl、sr都从车辆的底层CAN网获取，所有数据的采样周期都为0.1 s.

3.2 操控基元的表征

基于GMM表征的操控基元能够实现对行进间转向区间各操控位置概率密度的表征。具体地，在基于离合器的有级转向履带车辆中(见图7(b))，以左侧转向为例(右侧的转向离合器Lr始终处于结合状态，制动器Tr始终处于分离状态)，直驶操控基元是指Ll完全结合，Tl完全分离；原地转向操控基元是指Ll完全分离，Tl完全结合；在这两个转向之间的转向操控区间为行进间转向，利用GMM模型实现操控基元的划分表征。在基于二级行星转向机的有级转向履带车辆中(见图8(b))，以左侧转向为例(右侧的转向离合器Lr始终处于结合状态，转向制动器Zr始终处于分离的状态，停车制动器Tr始终处于分离状态)，直驶操控基元是指Ll结合，Zr和Tr分离；原地转向操控基元是指Ll分离，Zl分离，Tl完全制动；在直驶与原地转向之间的转向操控区间为行进间转向，利用GMM模型实现操控基元的划分表征，特殊的第一位置转向操控基元是指Ll分离，Zl结合(以GMM模型表征结合的操控区间范围)，Tl分离。图9为离合器转向机与二级行星转向机在1挡和4挡情况下的左侧操纵控制量区间概率密度分布对比图。

图9 左侧操纵控制量概率密度分布对比Fig.9 Comparison of probability density distributions of left stick position

从离合器转向机和二级行星转向机两种机构的对比可以发现，由于二级行星转向机在行进间转向过程中提供了第一位置转向这一高确定性的规定转向半径运动，无论是1挡还是4挡，转向操控量都分别在54.69%和54.73%附近形成尖峰，说明驾驶员在行进间转向过程中更偏向于使用第一位置转向操控基元，并且触发规定转向半径转向运动的转向值范围分别集中在54.69%±1.42%和54.73%±1.38%区间范围内。

从结果对比图中还可以发现，无论是哪种形式的转向机构，当处于非规定半径转向操控基元下时，转向操控量区间的标准差都会显著增大，并且随着速度的提升，区间的均值点也会发生不同程度的移动，具体的数值分析如表1和表2所示。

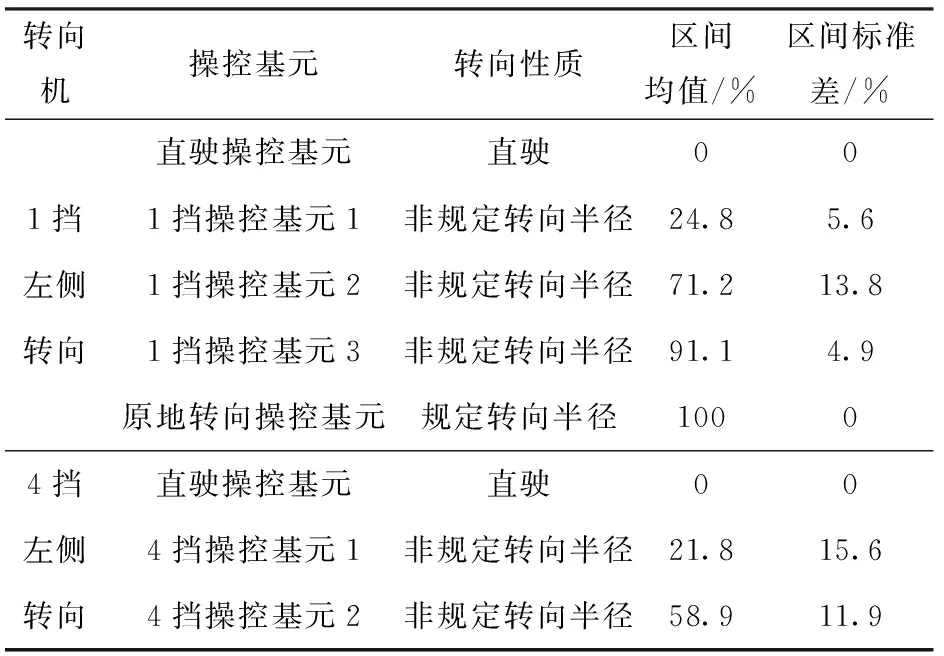
表1 离合器转向机转向操控基元表征

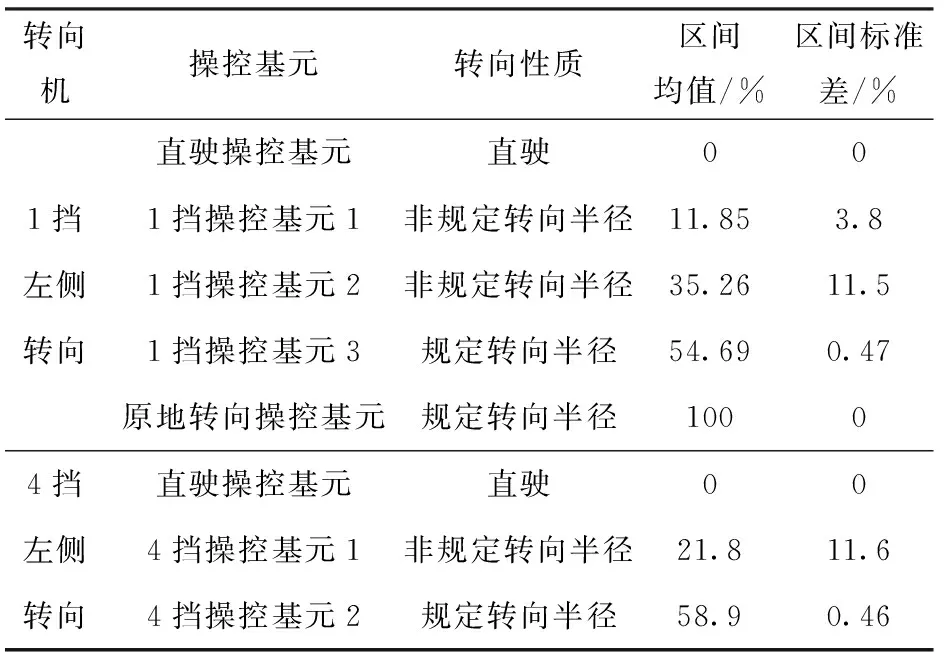
表2 二级行星转向机转向操控基元表征

从表3中可以看出，相对于离合器转向机，二级行星转向机在各个挡位下都具有更少的操控基元序列类别，这主要是因为二级行星转向机提供了两种确定度较高的规定半径转向操控基元，而离合器转向机仅有原地转向模式这一种规定半径转向操控基元。更多的规定半径转向操控基元选择会显著提升转向运动的确定性，避免因为转向过程不确定所导致的操控基元之间频繁切换，也因此大幅度降低了操控基元序列的类别个数。

3.3 操控基元序列的提取与类别辨识

基于最终所创建的各挡位下的全局操控序列图以及基于GMM聚类的序列图特征数组ψ，能够在对各挡位下操控基元序列进行提取的过程中完成对类别的辨识，各挡位下离合器转向机或二级行星转向机的操控基元序列类别辨识结果如表3所示。

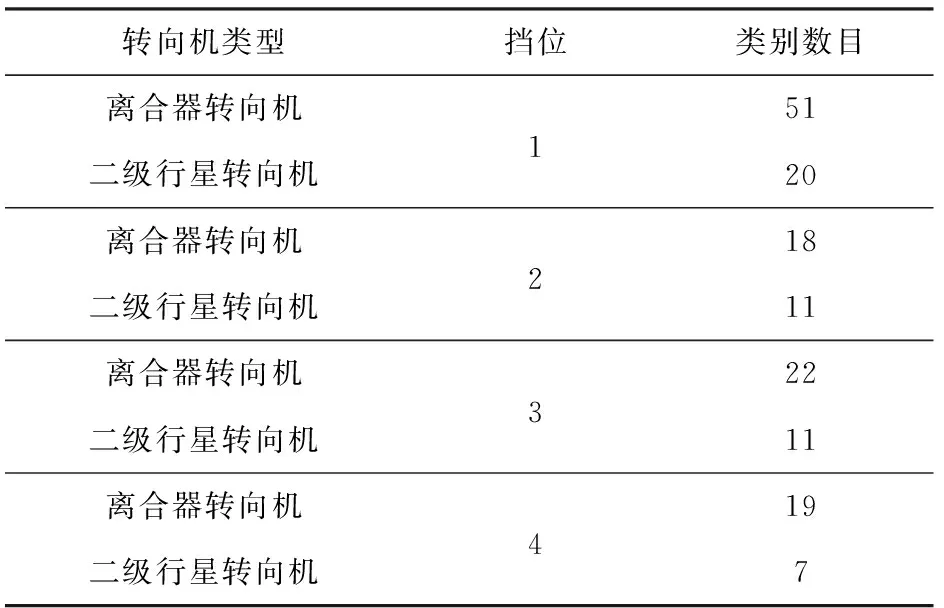
表3 操控基元序列类别辨识结果

由于后续驾驶员操控行为表征模型依赖于轨迹基元的提取结果进行数据重分组，以操控基元序列类别辨识为依据，对轨迹基元划分进行呈现。图10展示了基于二级行星转向机的有级转向履带车辆在1挡和4挡工况下的轨迹基元分割结果。

图10 轨迹基元类别辨识结果Fig.10 Recognition results of trajectory primitive class

从图10中轨迹基元划分的结果上来看，虽然本文采用非监督学习算法对轨迹基元的类别进行了辨识，但由于操控基元序列的引入，保证了每一个轨迹基元的起始点与终止点都为直驶状态，增强了轨迹分割结果的可解释性，为后续在无人行驶工况下与运动规划系统的整合提供了可能。

3.4 驾驶员操控行为的表征

图11 1挡驾驶片段驾驶员行为预测对比结果Fig.11 Comparison of predicted results of driver behavior for Gear 1 driving segment

图12 4挡驾驶片段驾驶员行为预测对比结果Fig.12 Comparison of predicted results of driver behavior for Gear 4 driving segment

从图11(b)、图11(c)和图11(d)、图11(e)以及图12(b)、图12(c)和图12(d)、图12(e)的对比中可以发现，考量轨迹基元与操控基元关联关系的预测结果在预测精度方面优于不考虑关联关系的预测结果。其中，在1挡工况下的平均预测值偏差为3.75个位置分度，是对比方案的76.75%；在4挡工况下的平均预测偏差为5.81个位置分度，是对比方案的90.82%. 此外，通过图11(b)、图11(c)与图11(a)以及图12(b)、图12(c)与图12(a)的比对结果可以发现，无论是哪种驾驶员行为预测算法，都多次将由于地面扰动所形成的航向偏差校正识别为直驶修正操控行为，继而产生了较大的预测偏差，但在其余工况下时考量关联关系的预测模型都能够准确辨识出操控行为基元。

从驾驶员操控行为预测不确定性的角度来看，在转向操控量零位、行进间第一转向位置与原地转向转向位置的预测不确定性较小，但在其余非规定转向位置存在较大的预测不确定性，这主要是因为非规定转向半径的操控基元自身存在较大的区间标准差(见表1和表2)。此外，另一个值得关注的细节是，如图11(b)和图11(c)的对比，以及图12(b)和图12(c)的对比，当转向操控量预测值处于第一转向位置时，左右两侧具有不相同的不确定度，左侧的不确定度在1挡工况下仅为右侧的8%，在4挡工况下仅为右侧的37.29%. 由于预测的不确定度与操控基元自身的区间标准差相关，从结果来看左侧操纵机构的第一位置转向精确到位能力较强，右侧操纵机构由于磨损等原因精确到位能力较差，这也与车辆的实际情况相对应。