基于改进VMD和深度置信网络的风机易损部件故障预警
2019-06-13郑小霞陈广宁任浩翰李东东
郑小霞,陈广宁,任浩翰,李东东
(1.上海电力大学 自动化工程学院,上海 200090;2.上海东海风力发电有限公司,上海 200090)
随着风力发电装机容量的不断扩大,风电快速发展的同时也面临着一系列的问题,由于风电机组结构复杂且往往处于恶劣环境,轴承、齿轮和转子等成为风机的易损部件。从风机故障导致的风机停机时间和维护成本上看,来自机械易损部件的故障影响最大。因此对这些部件的故障预警可以及时掌握机械故障趋势,合理安排维修策略,对提高风电场运行的可靠性和经济性具有重要意义[1]。
风能的随机性使得风电机组设备状态数据动态性强、非平稳特征明显、所含频率成分复杂且受转速影响而不断发生变化,谐波、干扰与故障特征频率之间很容易出现重叠,传统的经验模式分解难以准确提取故障特征信息。变分模态分解(Variational Mode Decomposition,VMD)是由Dragomiretskiy等[2]提出的一种自适应信号处理方法,该方法通过不断迭代,在若干频域带宽中更新获得新的各模态分量,重构给定信号。刘长良等[3]通过将变分模态分解与奇异值分解相结合,提取出故障特征,为滚动轴承故障诊断提供参考。唐贵基等[4]通过对变分模态分解中分解个数和惩罚因子进行参数优化,放大滚动轴承早期故障的微弱特征信息。赵洪山等[5]提出了基于变分模态分解和奇异值分解降噪的故障特征提取方法,通过变分模态分解对信号进行重构,从而提高信噪比,突出故障特征,提高滚动轴承故障诊断效果。
分解后的故障信号受到各种运动参数的影响使得信号成分仍十分复杂难以识别,必须有适当的模式识别算法才能有效发挥VMD的优势进而完成故障的预警。深度置信网络(Deep Belief Network,DBN)是Hinton等[6]提出的一种深度学习网络,其训练算法中结合了有监督学习和无监督学习的优势。李艳峰等[7]将奇异值分解与DBN分类器件进行结合,对滚动轴承的故障类型和故障程度做出稳定、准确的识别。李巍华等[8]将DBN直接应用于轴承信号处理,实现轴承故障的分类识别,并有效控制了DBN的计算成本。
本文针对风机关键部件振动信号特征微弱难以提取的问题,将原始振动信号用VMD算法处理得到若干本征模函数,并对其进行特征提取构成深度置信网络的高维输入向量,通过深度置信网络分类器实现风机部件故障状态的识别。通过对实验数据和现场信号的分析,该方法可有效地对故障类型做出准确的识别,对风机部件早期故障预警具有实用性。
1 变分模态分解及其改进
1.1 变分模态分解算法介绍

(1)
同样的,模态分量的中心频率取值问题的解为
(2)
式中:{uk}={u1,u2,…,uK},{ωk}={ω1,ω2,…,ωK}为各分量及其中心频率。
VMD算法流程如下:

步骤2n←n+1,并根据式(1)和式(2)更新uk和ωk;
步骤3更新λ
(3)

1.2 对变分模态分解的改进
变分模态分解在处理信号时需要预先设定好模态分量的分解个数,并且研究发现,算法中的惩罚因子的选取对于分解效果也有很大的影响。因此,选取适当的参数,对VMD算法处理故障信号效果影响较大。
1.2.1 基于相关系数的分解个数确定
以美国凯斯西储大学电气工程实验室的滚动轴承数据实验为例。选用的滚动轴承为正常工作下的SKF 型深沟球轴承,振动数据采样频率为12 kHz、电机负载为2.237 kW、转速为1 730 r/min。用选取不同模态个数K值的VMD算法对轴承振动信号进行处理,得到结果如图1所示。
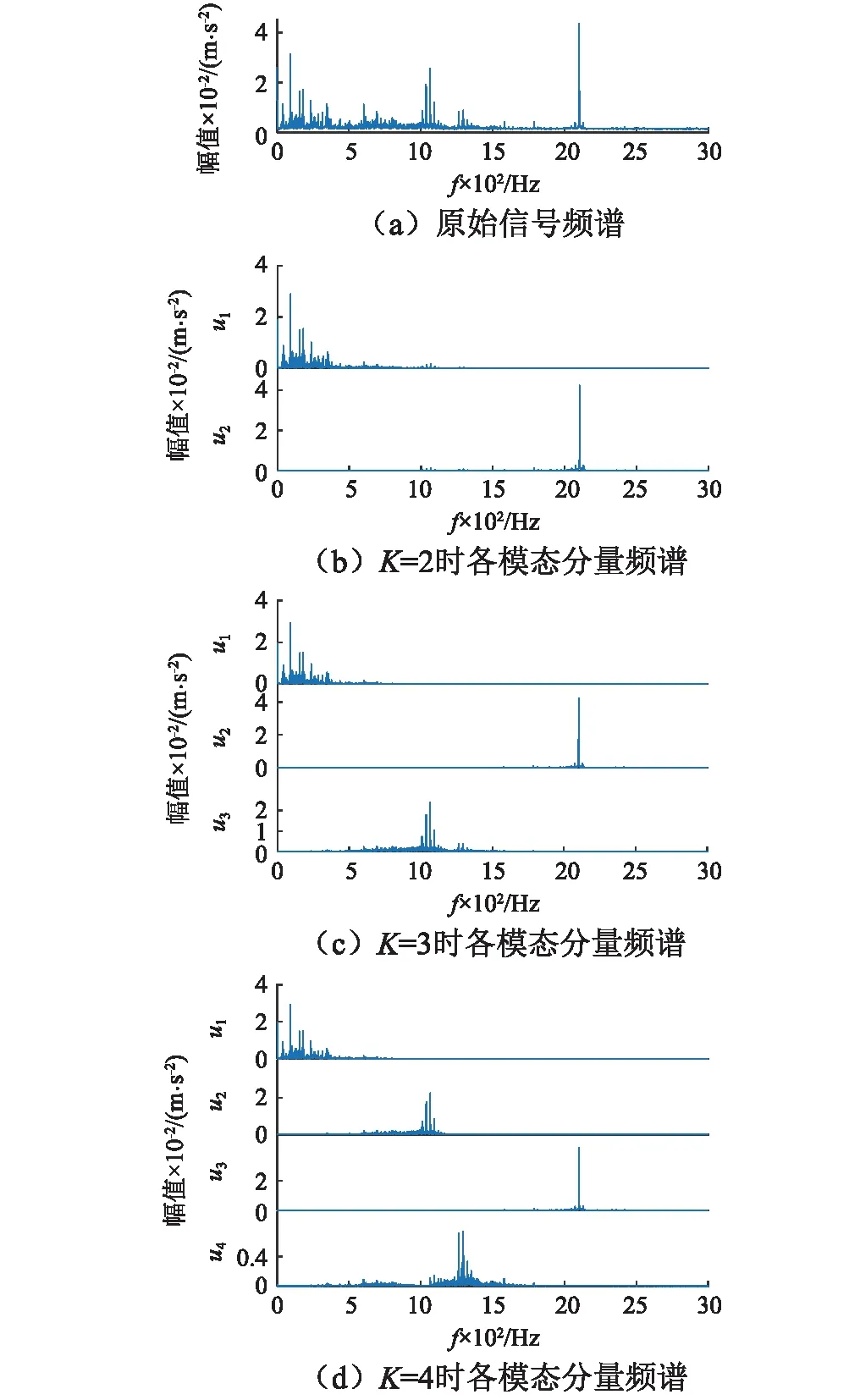
图1 原始信号和不同K值时各模态分量频谱Fig.1 The original signal and spectrum of various modal components at different K values
可以看到,K=2时模态分量中缺少了1 000 Hz频段的模态分量,存在信息缺失;而K=4时,模态分量u2和u4的中心频率相互靠近,产生频率混叠现象。
由此可见,K值较大时,会使频率集中在一个范围的信号被分解为若干的模态分量,使得其中心频率会比较靠近,产生频率混叠;K值较小时,由于VMD算法相当于自适应维纳滤波器组,原始信号中的一些关键信息会被滤波器滤掉,造成信息缺失。
基于以上问题及分析,本文提出了基于相关系数的模态个数确定方法。在分量中出现了最大中心频率的前提下,计算模态分量之间的相关系数,判断各模态分量之间是否存在频率混叠现象,从而确定模态个数。
信号x(n)和信号y(n)的相关系数定义为[9]
(4)
式中:分母为x(n),y(n)各自能量乘积的开方。VMD算法优化步骤如下:
步骤1初始化K=3,并用VMD算法处理原始信号;
步骤2计算各个模态分量之间的相关系数,提取其中最大的相关系数;
步骤3K←K+1,并根据步骤2更新模态之间的最大相关系数;
步骤4重复步骤3,直到最大相关系数超过阈值(经过大量实验分析,最大相关系数的阈值选取0.1较为合适),结束循环操作,最终K←K+1。
依旧选取前文滚动轴承数据,采用基于相关系数确定分解个数的方法,结果如表1所示。

表1 不同K值下的最大相关系数Tab.1 Maximum correlation coefficients at different K values
可以看到当K=4和K=5时,模态之间的相关系数的最大值均超过阈值,故确定模态个数K= 3。
1.2.2 基于PSO算法优化的惩罚因子确定
VMD算法中惩罚因子α对分解结果也有较大影响,研究发现:惩罚参数α越小,得到的各IMF(Intrinsic Mode Function)分量带宽越大,反之,α越大各分量带宽越小[10]。
粒子群算法[11]是一种群体智能优化算法,具有良好的全局寻优能力。算法通过更新粒子局部最优值和全局最优值自动筛选最优粒子,获得全局最优值。
包络熵是一种表述信号稀疏特性的标准,通过将信号解调后的包络信号处理成一个概率分布的序列pj,从而计算出熵值。信号x(j)的包络熵可以表示成
(5)
(6)
式中:a(j)为x(j)hillbert解调后的包络信号。
用VMD算法对原始信号处理之后,若得到的模态分量中包含噪音成分较多,其包络熵较大;相反,若分量中噪音成分较少,分量周期振动会更有规律性,包络熵也会较小。将第i个粒子代表的惩罚因子α代入VMD算法中,得到的所有模态分量的包络熵,并将包络熵最小值作为寻优过程中的适应度函数值,以适应度值最小化作为优化目标,优化步骤如下所示:
步骤1初始化各个参数和粒子的位置与初始速度,并将模态分量的包络熵最小值作为适应度函数;
步骤2在每个粒子的位置上对信号做VMD算法处理,并求取每个粒子的适应度函数值;
步骤3更新粒子的局部最优值和种群全局最优值;
步骤4根据式(11)、式(12)更新粒子位置和速度;
步骤5转至步骤2循环,直到迭代次数满足最大迭代次数,结束迭代,输出最优粒子的位置。
选取前文的美国凯斯西储大学电气工程实验室的滚动轴承数据,并对粒子群算法初始化如表2所示。

表2 粒子群算法参数初始化设定Tab.2 Initialization of parameters of PSO
粒子群算法中适应度函数随着迭代变化,如图2所示。从图2可知,粒子群算法在第5代时搜寻到最优值,搜寻到的最优惩罚因子α为921,原始信号由VMD分解后的效果如图3所示。

图2 适应度函数值随迭代变化图Fig.2 The fitness value changes with the iteration
1.3 特征提取
将原始信号通过VMD算法分解之后,对模态分量进行特征提取,不同故障类别的振动信号在其振动变化大小和时间复杂度上会有不同的反映,而提取单一的特征会使得识别准确率较低。通过大量的实验分析计算可知,均方根值可以反映振动信号在时域上的幅值变化,而排列熵可以通过比对相邻时间段的数据来度量一维时间序列的复杂性,因此本文选取模态向量的均方根值和排列熵来构造样本的特征向量,从而有效的表征出不同部件振动信号的故障状态。

图3 轴承原始信号及VMD分解图Fig.3 Original signal of bearing and VMD decomposition diagram
均方根值xrms作为一种反映信号波动大小的指标被广泛应用,表达式为
(7)
排列熵是一种衡量一维时间序列复杂度的平均熵参数,具有计算简单、抗噪声能力强、计算值稳定等优点[12-13]。
排列熵的算法原理如下:对一维序列X(i)进行相空间重构,即变为一个二维矩阵
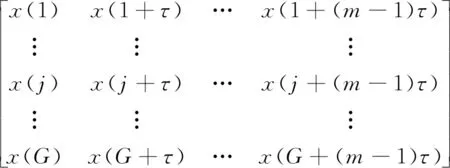
(8)
式中:m为嵌入维数;τ为延迟时间;G为重构向量的个数。矩阵中的每一行都是重构向量,使每一个重构向量重新依照大小进行升序排列,求得元素索引值按照元素大小排列的序列,统计每一种排列出现的次数,从而得到每一种排列顺序出现的概率,构成一组序列[P1,p2,…,Pl,…,Pm!],其中Pl为第l种排列出现的概率,排列熵的表达式则表述为
(9)
对排列熵归一化为
PE=PE(m)/ln(m!)
(10)
2 基于改进VMD和DBN的故障识别
DBN由多层无监督的RBM网络和一层有监督BP神经网络构成,其训练算法分为两个步骤,即预训练(pre-training)和微调(fine-tuning)。这样的训练方式使DBN避免陷入局部最小值,也使训练效率大大提高。
2.1 预训练阶段
受限波尔兹曼机(Restricted Boltjman Machine,RBM)是DBN的主要组成部分,其模型的能量函数形式为
(11)
式中:θ={wij,ai,bj}为RBM需要确定的模型参数;wij为可视层第i个神经元和隐含层第j个神经元的连接权值;ai和bj分别为可视层第i个节点和隐含层第j个节点的偏置值。基于该能量函数,可以得到(v,h)的联合概率分布
p(v,h|θ)=e-E(v,h|θ)/Z(θ)
(12)
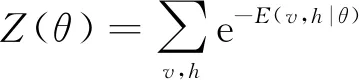
对RBM的参数θ={wij,ai,bj}进行训练,拟合输入的训练数据,并采用对比散度(Contrastive Divergence,CD)算法对参数θ进行更新。
2.2 微调阶段
BP网络的训练分为前向传播和后向传播。前向传播将输入向量逐层处理,传到输出层,并把输出值与期望值对比;在后向传播中,将实际输出值与期望输出值的差值从输出端向输入端反向传播,实现DBN参数微调,从而进一步减少训练误差。
本文提出基于DBN的故障信号识别方法,首先将原始信号用参数优化后的变分模态分解处理后得到若干模态分量,对每个模态分量提取出排列熵和均方根值后,构成特征向量输入到DBN分类器中进行故障识别。故障诊断流程图如图4所示。具体步骤如下:
步骤1分别对滚动轴承在各个工作状态下进行采样,得到不同状态下的轴承振动数据;
步骤2用参数优化后的VMD算法每个状态下的振动数据进行处理,得到若干模态分量;
步骤3对每个模态分量求取排列熵和均方根值,构成若干个多维特征向量;
步骤4将多维特征向量输入到DBN模型中进行训练,得到不同状态下的深度置信空间的预测模型;
步骤5把测试振动数据进行步骤2、步骤3操作之后输入到训练好的DBN模型中,得到预测的故障类型。
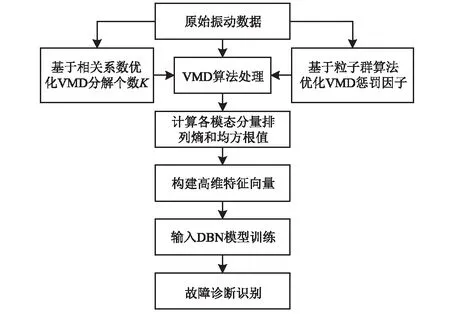
图4 滚动轴承故障诊断流程图Fig.4 Flow chart of rolling bearing fault diagnosis
3 实验信号分析
3.1 实验台参数及采样参数
为验证本文提出的方法对实际振动信号处理的有效性,利用实际动力传动故障实验台进行了验证。实验台传动系统主要包括主轴、一个二级行星齿轮箱、一个二级平行齿轮箱、一个轴承负载以及一个可编程的磁力制动器,风机传动系统故障模拟平台如图5所示。滚动轴承的故障上通过电火花加工的方式人为植入,分别模拟出滚动轴承内圈故障、外圈故障、滚动体故障3种故障状态。实验中设定驱动电机转频为40 Hz状态,加速度传感器安装在二级行星齿轮箱外壳上,采样频率为12 kHz,采样点2 048个为一组,共3 600组采样数据,3种故障状态及正常状态各900组数据。实验轴承结构参数如表3所示。

图5 风机传动系统故障模拟平台Fig.5 Fan drive system fault simulation platform

表3 轴承结构参数Tab.3 Bearing structural parameters
在实验数据中随机抽取30%作为训练样本,其余作为测试样本,从而得到正常状态、内圈故障、外圈故障、滚动体故障4种状态轴承振动数据训练样本各270组,以及测试样本各630组。本文4种状态下0~1 s的实测信号如图6(a)所示。从各种状态的振动信号时域图中可以看到故障轴承振动中含有冲击特征,但从时域波形很难对于轴承状态做出准确区分,需要用信号处理方法提取关键的特征信息。
而从图6(b)可知,内圈故障与外圈故障的频率成分较为相似,在故障诊断中容易发生混淆。

图6 实测振动信号图Fig.6 Measured vibration signal diagram
3.2 VMD参数优化
利用本文提出的基于分量间的相关系数确定VMD算法分量个数K,随机抽取一组轴承正常信号。由于K为3时,存在信息缺失问题,所以K的取值从4开始。K取4,5,6,7,8时,分量之间的最大的相关系数如表4所示。从表4可以知,当K取7,8时,信号经VMD算法分解之后分量之间的最大相关系数均大于阈值0.1,而取4,5,6时,皆小于阈值。因此选取K值为6。

表4 不同K值的最大相关系数Tab.4 Maximum correlation coefficients at different K values
确定了VMD算法分解个数之后,再确定VMD算法的惩罚因子α取值。随机抽取一组轴承正常信号,用粒子群算法优化惩罚因子使分量的包络熵达到极小值。从图7可以看到当迭代达到第8次时,分量局部极小包络熵值达到收敛,最终惩罚因子α选为1 586。

图7 局部包络熵极小值随迭代变化图Fig.7 Minimum variation of envelope entropy with iteration
3.3 特征提取
VMD算法参数优化之后,将原始信号通过VMD算法进行分解,每一组信号都分解为6个模态分量,对每一个模态分量进行特征提取。在求取模态分量的排列熵时,由于时延τ的变化对于信号排列熵值的影响较小,所以本文设定时延τ为1。嵌入维数m较小时无法准确反映信号动力学突变现象;当m取值过大,排列熵的计算量增大并且重构信号的索引号排列顺序趋于简单[14],Christoph等[15-16]研究指出当嵌入维数m在5~7取值时,排列熵能够准确的反映时序序列的动态特性。本文设定嵌入维数m为6。
求取其排列熵和均方根值后,将其组合构成高维特征向量,共得到270组12维的特征向量。其特征向量的平均值,如图8所示。
3.4 DBN分类器训练
将训练信号模态分量特征提取后构成的高维特征向量输入到DBN分类器中,因为每一组训练信号的特征向量有26维,且对4种状态进行分类,则设置DBN的第一层RBM的可见层有12个节点,最后一层BP网络的输出层有4个节点。本文建立的DBN共一个RBM网络和一个BP网络构成,RBM网络的隐含层节点数为20,即DBN分类器的结构为12—20—4,DBN的学习率设定为0.1。
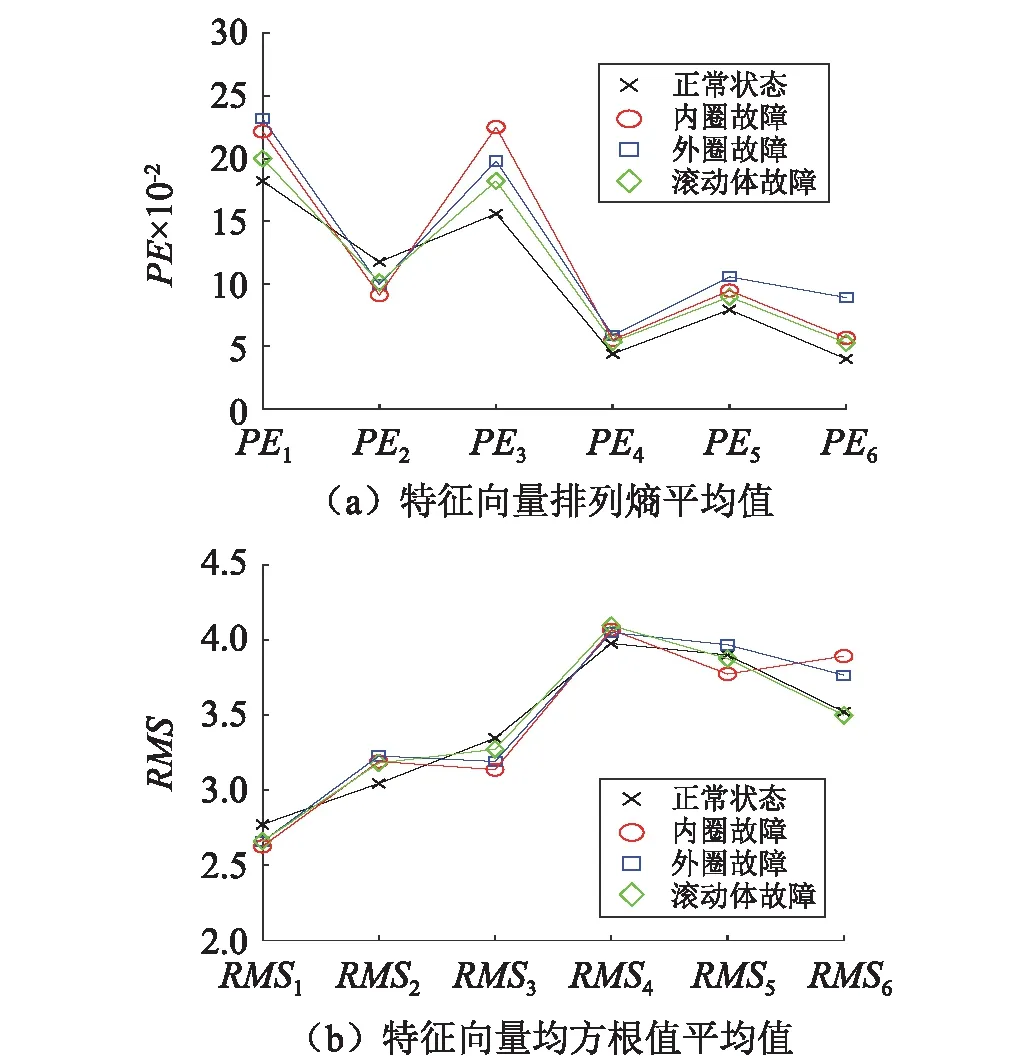
图8 特征向量平均值Fig.8 Eigenvector mean
DBN分类器模型训练好后,将630组测试数据输入到分类器中进行分类,识别准确率为96.6%,DBN的分类结果如表5所示。
从表5可知,内圈故障和外圈故障在诊断时互相错认的情况是所有故障识别错误的情况里最多的,这也与之前的理论分析相吻合。
为了与VMD算法在故障诊断中信号处理的效果形成对比,本文将上述同样的测试信号用EMD进行分解,并选取EMD方法分解出的前6个模态分量,进行同样的特征提取方法和特征向量构成方法,输入到相同的结构的DBN分类器中训练并对测试信号进行分类。采用EMD方法分解信号的故障诊断准确率如表6所示。

表5 基于VMD和DBN的滚动轴承故障识别结果Tab.5 Fault identification of rolling bearing based on VMD and DBN

表6 基于EMD和DBN的滚动轴承故障识别结果Tab.6 Fault identification of rolling bearing based on EMD and DBN
从表6可知,相对于VMD算法,采用EMD算法的轴承故障诊断在识别的准确率上有着明显降低,这是因为实验平台实际运行中会有噪声的影响,VMD算法中嵌入了自适应维纳滤波器组,对于噪声有着较好的鲁棒性,而EMD算法无法在有较强噪声的环境下对信号进行有效的处理,在信号分解之前需要对原始信号进行滤波处理。这也进一步证明了VMD算法在轴承故障诊断上的优越性。
4 现场信号分析
由于实验信号为实验室环境采集的规整信号,且振动信号往往来自于已经产生较为明显故障的机械部件,为了进一步验证方法的可靠性,并使该方法运用在早期故障轻微的时期,对风机易损部件进行故障预警,本文选取某风电机组齿轮箱高速轴的振动数据。齿轮箱传动结构为两级行星、一级平行传动。通过安装在齿轮箱外箱体轴向和径向上的加速度传感器采集振动信号,采样频率25 000 Hz,齿轮箱轴承图和现场测点布置示意图,如图9和图10所示。分别测取风机现场中轴承损坏、齿轮轻微磨损、齿轮严重磨损、齿轮啮合不良和正常状态下的振动信号各200组,并随机选取其中的25%作为训练信号,每组信号轴向信号和径向信号各有2 048个采样点,从而对轴承严重故障、轻微故障、未发生故障但啮合不良等各个状态进行识别诊断,从而达到故障预警的作用。图11为各个状态下随机抽取一组振动信号的时域图。
选取一组正常状态下的信号,运用本文方法对VMD参数进行优化,通过表7可知,当VMD分解个数取5时,轴向信号和径向信号的分量间的最大相关系数都超过阈值0.1,故将轴向振动信号和径向信号分解为4个模态分量;通过PSO(Particle Swarm Optimization)算法优化VMD算法惩罚因子,优化后轴向信号的VMD惩罚因子取值为193,径向信号的VMD惩罚因子取值为97。
由于每组信号中包含有轴向和径向两类信号,并分别分解为4个模态分量,对每个模态向量求取均方根值和排列熵,因此构成的特征向量具有2×4×2维。
将特征向量输入DBN分类器中进行训练,由于每组特征向量有16维,且要求DBN对5种工作状态进行分类,因此第一层RBM的可见层节点数为16,最后一层BP的输出层节点数为5。建立的DBN由一个RBM网络和一个BP网络构成,RBM网络的隐含层节点数为20,即DBN分类器的结构为16—20—5,DBN的学习率设定为0.1。训练好DBN后,对750组测试信号求取特征向量,输入到训练好的DBN中进行分类,分类结果如表8所示。

图9 齿轮箱第三级轴承Fig.9 Gearbox level three bearing

图10 现场测点布置示意图Fig.10 Layout of site survey points

表7 不同K值下分量间最大相关系数Tab.7 Maximum correlation coefficients at different K values
从表8可知,本文方法对现场实际信号的故障识别准确率达到了97.5%,而齿轮严重损坏、齿轮轻微磨损、齿轮啮合不良的识别率分别为97.3%,99%,91%,从而证明了该方法在不同故障程度的识别准确性,起到了易损部件的故障预警作用,进一步验证了该方法的可靠性。其中故障识别错误的情况基本来自于齿轮高速轴磨损和齿轮啮合不良这两种状态之间,这是由于齿轮高速轴磨损时,齿轮箱高速级啮合频率附近会有明显的高速轴转频,易与啮合不良状态发生混淆。

表8 基于VMD和DBN的现场信号故障识别结果Tab.8 Fault identification results of field signals based on VMD and DBN
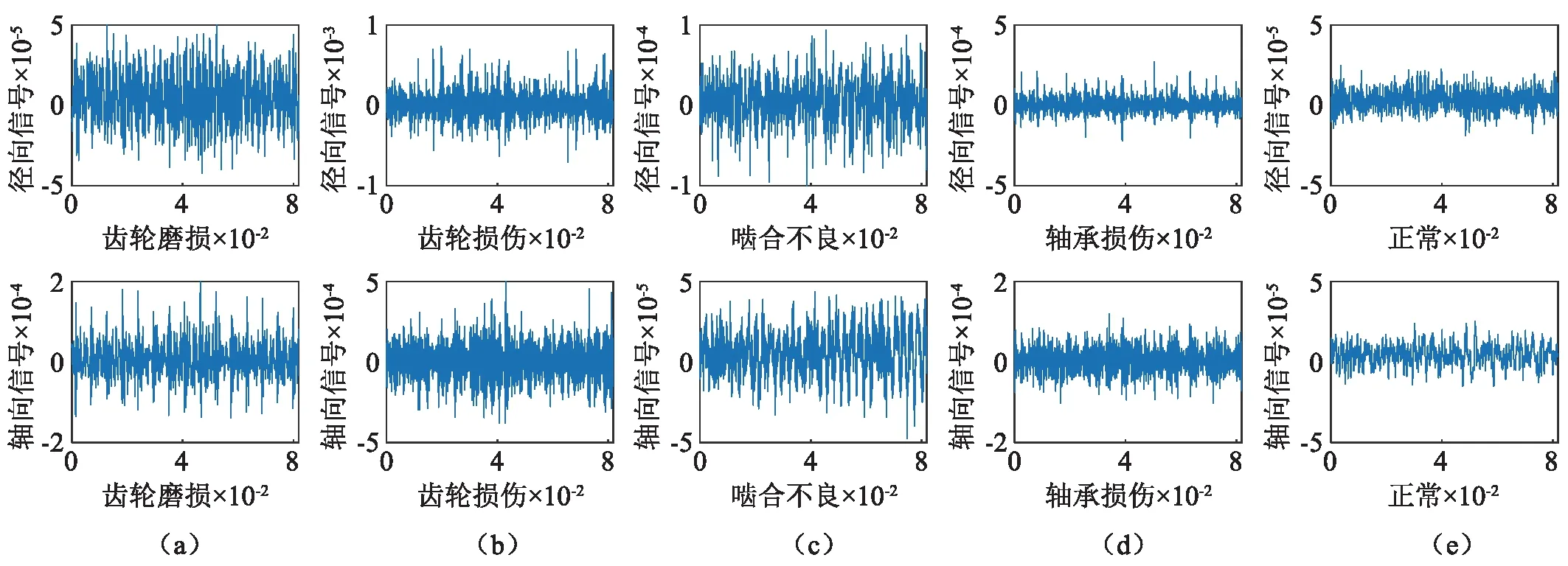
图11 现场振动信号时域图Fig.11 Time domain diagram of field vibration signal
5 结 论
本文针对风机易损部件早期故障特征难以提取的问题,提出变分模态分解与深度置信网络的故障预警方法,将改进的变分模态分解用于故障振动信号,求取排列熵和均方根值并构成特征向量输入到深度置信网络分类器中进行训练,并通过实验信号和实际信号验证了其在早期故障预警中的可行性,提高了风机易损部件故障预警的准确性。
