两招，轻松解决抽象函数的定义域

理解函数定义域的概念，会求函数的定义域，是高中数学一个最基本的技能，毕竟“定义域优先”。所有与函数相关的问题，都要首先考虑定义域，避开定义域去谈函数问题，就像是火车脱轨，失去正确的方向。

求函数的定义域问题一般分为两大类：求具体函数的定义域和求抽象函数的定义域。在此，笔者结合自身的教学经验，和大家分享求抽象函数定义域的解法。

首先，我们有必要来明确定义域的概念，只有理解好定义域的真正含义，才能更轻松求解函数的定义域。人教版数学必修第16页中对函数的定义域有了明确的概念：函数y=f(x)，x∈A，其中，x叫做自变量，x的取值范围A叫做函数的定义域。

下面我们先看三道题。

例 1.已知函数 y=f(x)的定义域为(3，5)，求函数 y=f(2x+1)的定义域。

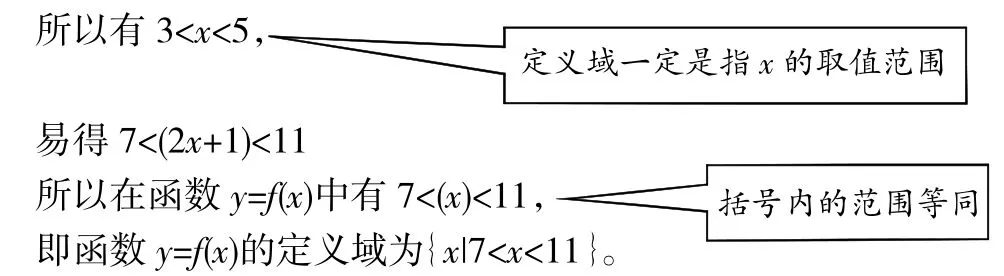
例 2.已知函数 y=f(2x+1)的定义域为(3，5)，求函数 y=f(x)的定义域。

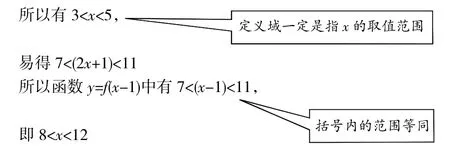
例 3.已知函数 y=f(2x+1)的定义域为(3，5)，求函数 y=f(x-1)的定义域。

现在，我们就运用第一招“定义域一定是指x的取值范围”去读题，看看题目告诉了我们什么，又问我们什么。

例 1.已知函数 y=f(x)的定义域为(3，5)，求函数 y=f(2x+1)的定义域。

题目告诉我们：y=f(x)中，x的范围是3

题目问我们：y=f(2x+1)中的x的范围

例 2.已知函数 y=f(2x+1)的定义域为(3，5)，求函数 y=f(x)的定义域。

题目告诉我们：y=f(2x+1)中，x的范围是3

题目问我们：y=f(x)中的x的范围

例3.已知函数y＝f(2x+1)的定义域为(3，5)，求函数y=f(x-1)的定义域。

题目告诉我们：y=f(2x+1)中，x的范围是3

题目问我们：y=f(x-1)中的x的范围

我们用第一招“定义域一定是指x的取值范围”就轻松读懂了题意。

然后，我们就运用第二招：“括号内的范围等同”去解题。

例 1.已知函数 y=f(x)的定义域为(3，5)，求函数 y=f(2x+1)的定义域。

分析：函数y=f(x)中，x的范围是3

解：因为函数 y=f(x)的定义域为(3，5)，

所以函数y=f(2x+1)的定义域为｛x|1

例2.已知函数f(2x+1)的定义域为(3，5)，求函数y=f(x)的定义域。

分析：f(2x+1)中的x的范围为3

解：因为函数 y=f(2x+1)的定义域为(3，5)，

例 3.已知函数 y=f(2x+1)的定义域为(3，5)，求函数 y=f(x-1)的定义域。

分析：函数y=f(2x+1)中的x的范围为3

解：因为函数 y=f(2x+1)的定义域为(3，5)，

所以函数y=f(x)的定义域为｛x|8

纵观这三道题，其实就是求抽象函数定义的三大类型题：

已知函数y=f(x)的定义域(m，n)，求函数y=f(g(x))的定义域；

已知函数y=f(g(x))定义域(m，n)，求抽象函数y=f(x)的定义域；

已知函数y=f(g(x))定义域(m，n)，求复合抽象函数y=f(h(x))的定义域。

以后遇到抽象函数的问题就可以模仿上面三个例子，先运用第一招“定义域一定是指x的取值范围”去读清题意，再运用第二招“括号内的范围等同”去解题，则抽象函数的定义域问题就轻松解决了。