嵌套函数中降维思想的应用和拓展

一、问题的提出

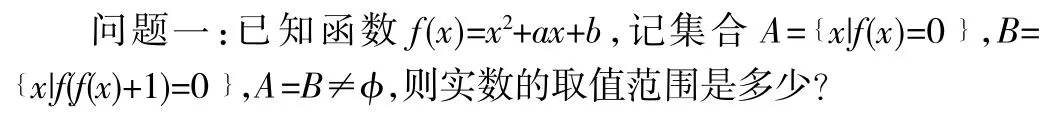
二、问题的解决

【分析】显然f(f(x))是一个四次多项式，f(x)是一个二次式，又A=B，所以多项式f(f(x))中必定含有因式f(x)，于是可以通过配凑化简多项式f(f(x))，从而把f(f(x))=0这个四次方程转化成两个二次方程的乘积。

综上0≤a<4

【点评】上述解析中通过两步即可完成

Step1：对f(f(x))进行配方，丢掉部分项，实现降维降次

Step2：通过集合运算理清互相之间的关系

【拓展】如果把方程右边的0换成其他实数或者变量，这种方法还通吗？

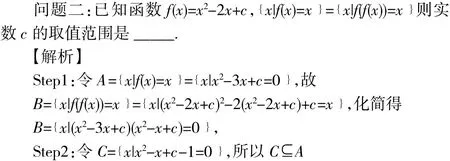
【点评】这里如果把集合中方程改成不等式，又如何呢，事实上就成了本文开头那个学考题了

【解析】

综上所述得-2≤a≤2

【小结】上述三个问题的解决其本质就是把多项式配方化简，丢掉部分项，实现降维降次，从而转化成低次的代数运算

【拓展】本题中集合中不等式右侧把换成其他数，可行吗？依然可以

三、问题的推广

【小结】只要题干中有，那么高次多项式就一定有一个因式是低次多项式，于是问题就转化为两个等次方程(或不等式)的问题了，后面的问题用集合的运算关系比较容易说明。

四、问题的延伸

不同实根，则实数a的取值范围为______.

解析：由 f(f(x))=f(x)知，f(f(x)）-f(x)中必有因式 f(x)-x

配方

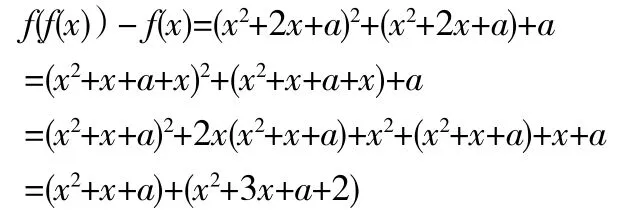
上式要有3个实根，

故两方程有一个公共根或者一个方程有两个相等的实数根

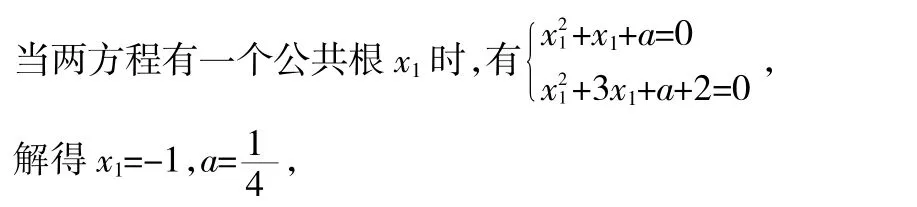
此时正好有三根，满足题意。

当一个方程有两个相等的实数根时或，得，

综上所述a=0

浙江省高考《数学考试》对于运算求解能力主要考查对算式进行的计算、变形，对数值的估算和近似计算等的能力。进一步考查对条件分析、方向探究、公式选择、步骤确定等一系列过程中运算能力的求解。由此可知，平常在教学中加强对算式的适当变形可以让我们的教学更加快捷高效。