基于遍历微小单元法非直视非共面紫外光通信信道容量分析

宋鹏，苏彩霞，赵太飞，陈锦妮，朱磊，张晓丹

（1. 西安工程大学电子信息学院，陕西 西安 710048；2. 西安理工大学自动化与信息工程学院，陕西 西安710048）

1 引言

非直视紫外光（UV, ultraviolet）通信是通过200～280 nm“日盲”波段紫外光在大气中的散射来进行信息传输的一种新型无线光通信方式[1-3]。与传统的通信方式相比，紫外光通信具有保密性好、抗干扰能力强、全方位性、非直视通信[4]等优点，可应用于近距离保密通信，尤其适用于“电磁静默”条件下的装甲集群或舰船间的无线保密通信，在国防信息化建设中具有广阔的应用前景。

建立紫外光通信系统的信道传输模型是研究信道容量的基础。1979年，美国麻省理工学院Reilly等[5]基于椭球坐标系建立了经典UV单次散射信道传输模型。随后，文献[6]在文献[5]的基础上对公共散射体进行分区域积分，建立了紫外光共面单次散射通信模型。文献[7-8]提出了紫外光共面单次散射经验路径损耗模型，并给出了经验路径损耗计算的部分参数。文献[9]根据紫外光单次散射传输模型，分析了大气中紫外光散射效应对脉冲响应信号展宽的影响和脉冲响应序列串扰对通信速率的限制。文献[10]搭建了紫外光非直视通信实验平台，给出了共面条件下脉冲宽度的不同计算方法，并研究了脉冲响应信号与收发端几何参数之间的关系，得出了脉冲展宽与发散角关系不大的结论。文献[11]利用伽玛函数模拟了信道脉冲响应，给出了带宽计算式，不足之处是不容易确定带宽计算式中的参数。文献[12]建立了非直视紫外光链路带宽的解析模型。文献[13]给出了紫外光直视通信系统的信噪比计算式。文献[14]基于非直视紫外光单次散射传输模型，提出了接收端信噪比估算方法，给出了系统信道容量，并对共面情况下紫外光通信系统的信道容量进行了研究，而在实际的通信过程中，紫外光的发射端与接收端通常是非共面的，因此研究非直视非共面紫外光通信系统的信道容量是十分必要的。

文献[15]基于球面坐标系建立了紫外光非共面单次散射路径损耗模型，但是非共面公共散射体的边界较为复杂，需要对三重积分的上下限进行更细致的划分。文献[16-17]给出了紫外光非共面情况下路径损耗的近似闭合解，但是只适用于发散角和视场角很小的紫外光通信系统。文献[18]给出了收发端任意指向的遍历微小单元法路径损耗模型，该模型精度高、运算简便，能较好地适用于紫外光非共面单次散射通信系统。

本文根据文献[18]中的遍历微小单元法研究非直视非共面紫外光单次散射通信系统的信道容量。首先，基于球坐标系建立非直视非共面紫外光单次散射传输模型；其次，用遍历微小单元法计算接收端接收的能量，由接收能量推导出紫外光信道脉冲响应采样序列数学表达式；再次，通过对脉冲响应采样序列进行离散傅里叶变换得到系统的频率响应，求出系统的3 dB带宽，根据量子极限法求出系统的信噪比，进而用香农公式求出系统的信道容量；最后，仿真分析了系统带宽和信道容量与收发端仰角、视场角、通信距离、接收端偏轴角之间的关系，并给出结论。

2 遍历微小单元法紫外光非共面单次散射传输模型

传统的基于椭球坐标系的UV非直视非共面单次散射信道传输模型，由于公共散射体是不规则的多面体，因此对公共散射体进行三重积分上下限的取值不易确定，UV通信系统路径损耗的计算较复杂[15,19]。遍历微小单元法通过把不规则的公共散射体分割为大量的边界规则的微小的六面体，把复杂的积分运算转化为简单运算之和，能快速计算收发端任意指向的非直视非共面紫外光通信系统的路径损耗，便于嵌入式紫外光通信系统应用。

非直视非共面紫外光单次散射传播模型[20]如图1所示，其中，Ct和Cr分别为发射光束锥体和接收视场锥体，T和R分别为发射端和接收端，TE和RF分别为发射锥体的中轴线和接收锥体的中轴线，TE´和RF´分别为TE在x-y平面的投影和RF在x-y平面的投影，tφ和rφ分别为发射端发散角半角和接收端视场角半角，tθ和rθ分别为发射端仰角和接收端仰角，tα和rα分别为发射端偏轴角和接收端偏轴角，d为发射端与接收端之间的通信距离。

假设发射锥体与接收锥体的公共部分为V，即图1粗线所圈定的范围，光子经过V中任意散射点S的散射到达R。在球面坐标系中，用(θ,α,r)表示S的坐标，θ、α和r分别为顶角、方位角和径向距离。ζ为S与R的连线与接收视场锥体中心轴的夹角，散射角βS为S处光子的入射方向与经S点散射后光子的出射方向的夹角，1r为S到R的距离。

遍历微小单元法的基本思想是基于球坐标系，选定包含公共散射体的尽可能小的边界规则的封闭区域，然后把封闭区域分成多个边界规则的微小单元。遍历封闭区域中全部的微小单元，对中心点包含在公共散射体内的每个微小单元进行三重积分，即求出T发出的紫外光经过每个微小单元散射到达R的能量，并对该能量累加求和，最终得到紫外光经单次散射到达接收端的总能量。

图1 非直视非共面紫外光单次散射传播模型

根据遍历微小单元法基本思想和图1，包含图1中公共散射体V的非直视共面紫外光单次散射传播模型如图2所示。图2中，边框ULOW粗虚线圈定的范围为闭合区域V′；边框UMOW粗实线圈定的范围为公共散射体V；闭合区域V′被分割成大量的微小单元V′，“×”是微小单元V′的中心；TP是发射锥体的中轴线；RQ是接收视场锥体的中轴线；P、Q点在x-y平面的投影为P´、Q´。

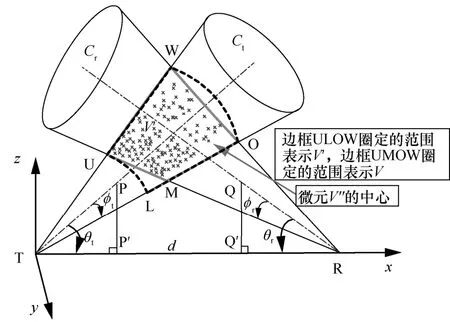
图2 非直视共面紫外光单次散射传播模型

闭合区域V′被分割成3M个微小单元V′，根据文献[18]中遍历微小单元法的误差与分割次数的关系，本文选取分割次数M=60。当被分割的微小单元的中心点在公共散射体V内时，经微小单元V′′散射的能量才能被接收端接收，此时接收端接收的经一个微小单元散射的能量可以表示为[18]（以中心为S点的微小单元V′为例）

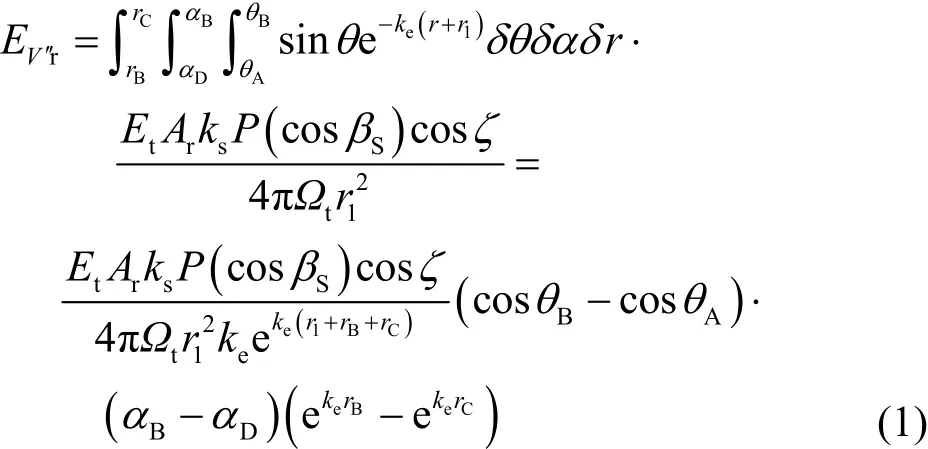
因为微小单元V′非常小，所以V′内散射点的散射角可以用V′中心散射点S的散射角近似表示，可计算为

对所有经过微小单元散射被接收端接收到的能量进行累加求和，可得到接收端接收的总能量为

根据遍历微小单元法，紫外光非直视通信系统的路径损耗为

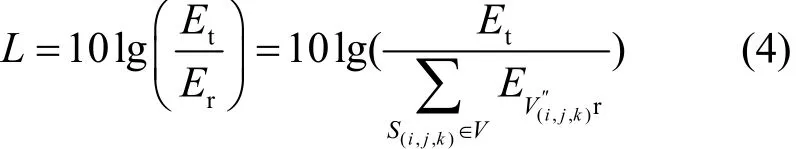
3 非直视紫外光通信系统的系统带宽与信道容量分析

3.1 用遍历微小单元法计算脉冲响应

设T发出一个能量为1 J的窄脉冲，如果一个光子从 T出发经V′散射到达 R 的时间ts在(Δt为定义的时间区间)内，则ts近似为tn。tn上的脉冲响应为经V′中每个V′的散射到达R的时间为tn的光子能量之和，由文献[18]可知，其计算式为

3.2 系统带宽与信道容量

3.2.1 系统带宽

由式(5)可以求出系统的脉冲响应采样序列，采样间隔为Δt。对脉冲响应采样序列进行离散傅里叶变换，可表示为[21]

其中，h(n)是系统的脉冲响应采样序列，N是脉冲响应采样点数，n=0,1,2,…,N-1，k=0,1,2,…,N-1，由式(6)求得频谱的频率分辨率为

系统3 dB带宽B可以根据式(6)求得系统的脉冲响应采样序列频谱图得到。

3.2.2 信道容量

紫外光通信系统中接收端的噪声主要包括信号光、背景光和暗电流引起的散粒噪声以及负载和放大器的热噪声。紫外光通信选择波长为 255 nm的“日盲”波段紫外光，因为大气分子特别是臭氧的强吸收作用，使“日盲”波段紫外光在地球表面的强度非常弱，加之接收端的滤光片会进一步滤除无用光，所以本文中忽略背景光噪声的影响。本文实验和仿真中选用滨松光子的R7154光电倍增管，环境温度为25℃，光电倍增管的阳极暗电流典型值为1 nA，比较小，因此忽略光电倍增管暗电流引起的散粒噪声。由于R7154光电倍增管增益为107，增益非常高，因此本文忽略器件热噪声的影响。本文只考虑信号光引起的散粒噪声，使用光电倍增管的直接检测系统趋近于检测极限，接收系统的信噪比可以用量子极限信噪比表示为[22]

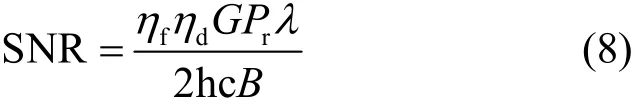
其中，λ为波长；dη为光电倍增管的探测效率；fη为滤光片透射率；h为普朗克常数；G=107为光电倍增管增益；c为光速；B为系统带为平均接收功率，其中tP为紫外光发射功率，L为路径损耗（单位为dB）。

综合分析，本文只考虑信号光引起的散粒噪声，系统的信道容量可以用香农公式[23]计算，如式(9)所示。

其中，SNR为信噪比，可由式(8)求得。

4 仿真结果分析

仿真条件：发送端发送能量为1 J的单脉冲信号，每个脉冲信号的脉冲宽度设为3 ns，起始时刻为 0，如不做特殊说明，系统仿真参数和收发端几何参数分别如表1和表2所示。

表1 部分系统仿真参数

表2 收发端几何参数

4.1 系统带宽

发送端脉冲宽度设为3 ns，脉冲响应采样点数N=100，采样间隔Δt=0.03 ns，tθ=10°，其他仿真参数如表1和表2所示。依据式(5)，接收端脉冲响应采样序列仿真曲线如图3所示。依据式(6)，可求得脉冲响应采样序列的幅度频谱如图4所示。依据式(7)，可求得谱分辨率Δf=4×106Hz。系统 3 dB带宽可以用脉冲响应5%最大值宽度的倒数表示[10]。由图3可知，系统3 dB带宽约为由图4可知，系统3 dB带宽约为40×106Hz，两者比较接近，均包括约10个Δf。为了提高精度，根据系统的脉冲响应采样序列的幅度频谱图求出本文系统3 dB带宽。

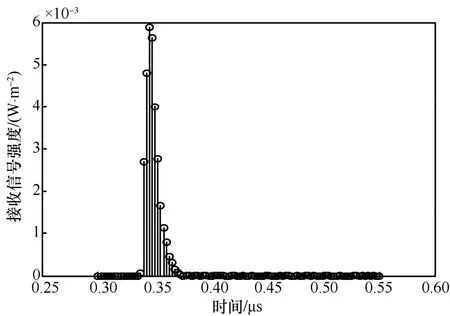
图3 脉冲宽度为3 ns时接收端脉冲响应采样序列

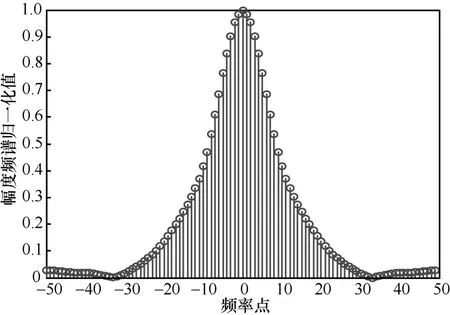
图4 脉冲宽度为3 ns时脉冲响应采样序列的幅度频谱

在非直视非共面紫外光通信系统中，随着通信距离的增大，系统的脉冲响应宽度变化较大，因而系统带宽变化较大。研究系统带宽与通信距离的关系是研究系统信道容量与通信距离关系的前提。

图5为系统带宽与通信距离的关系曲线，仿真参数如表1和表2所示。从图5可知，系统带宽随着通信距离的增大逐渐减小。当通信距离从10 m增大到50 m时，系统带宽快速减小，当通信距离从50 m增大到200 m时，系统带宽缓慢减小。

图5 系统带宽与通信距离的关系曲线

4.2 系统脉冲响应的实验验证

4.2.1 脉冲宽度为50 μs时的脉冲响应仿真与分析

遍历微小单元法脉冲响应的仿真波形如图6所示。仿真参数设置为：发射端发射单个脉冲信号，每个脉冲信号能量为1 J，起始时刻为0，为了便于与实验结果进行对比，脉冲宽度设为50 μs，发射端与接收端的仰角均为10°，发散角为6°，接收端视场角为80°，通信距离为20 m。从图6可知，脉冲响应的上升沿宽度为4 μs，下降沿宽度为8 μs，半最大值宽度为48 μs。

图6 脉冲宽度为50 μs时接收端脉冲响应仿真波形

4.2.2 实验验证

本文搭建的紫外光通信实验平台[24]如图 7所示。接收机采用高灵敏度光电倍增管（滨松光子R7154）；发射机采用中心波长 255 nm“日盲”紫外LED（美国SET公司生产的UVTOP系列）。实验时间为2017年1月23日20:00—23:00，实验地点为西安工程大学金花校区田径场，实验天气晴朗。具体的实验条件与参数如表3所示。

图7 非直视紫外光通信装置

表3 实验条件与参数

利用图7所示的紫外光通信实验平台得到的发射频率为10 kHz方波（脉冲宽度为50 μs）时接收端示波器输出信号波形如图8所示。图8的仿真参数与图6的仿真参数一致，通信距离为20 m，发射端与接收端仰角均为10°，发散角为6°，接收端视场角为80°，其他实验条件与参数如表3所示。从图8可知，脉冲响应信号的上升沿宽度为5 μs，下降沿宽度为10 μs，半最大值宽度为50 μs。

图8 发射频率为10 kHz（脉冲宽度为50 μs）方波时接收端示波器输出信号波形

相比实验结果，仿真结果的上升沿小1 μs，下降沿小2 μs，半峰全宽小2 μs，即仿真结果与实验结果能较好地拟合，这验证了用遍历微小单元法仿真系统脉冲响应的有效性。仿真与实验略有差别是因为实际实验环境比较复杂，光电倍增管的响应波长有一定的范围。

4.3 信道容量

UV系统通信距离、收发端仰角、发散角、视场角及收发端偏轴角会显著影响系统的路径损耗和脉冲响应，进而影响系统的信道容量。本节利用遍历微小单元法仿真分析非共面情况下，紫外光通信系统收发端几何参数对系统带宽以及接收端信噪比的影响，进而利用香农公式给出系统信道容量与收发端几何参数和通信距离的关系。

4.3.1 收发端仰角对系统信道容量的影响

收发端仰角对系统信道容量的影响如图9所示。图9(a)的仿真条件为：发射功率为50 mW，tθ以20°的步长从10°增加到70°，θr=45°，对于特定的tθ，d以20 m的步长从20 m增加到200 m，其他仿真参数如表1和表2所示。由图9(a)可知，信道容量随着d的增大而逐渐减小，d=60 m是信道容量变化的拐点，当d＜60 m时，信道容量快速减小，当d＞60 m时，信道容量缓慢减小。当tθ较小时，信道容量随着tθ的增大而快速减小，当tθ较大时，信道容量随着tθ的增大而缓慢减小，例如，tθ为50°和70°时的信道容量几乎相同。当tθ=10°，rθ=45°时，d=20 m处的信道容量是d=200 m处信道容量的10倍。

图9(b)的仿真条件为：tθ=45°，rθ以20°的步长从10°增加到70°，对于特定的rθ，d以20 m的步长从20 m增加到200 m，其他仿真参数如表1和表2所示。由图9(b)可知，系统信道容量随着rθ的增大而逐渐减小。当rθ＞50°时，rθ对系统信道容量的影响很小，例如rθ为50°和70°时的系统信道容量基本一致。对比图9(b)与图9(a)可得，当tθ和rθ均较小时，相比rθ，tθ的变化对信道容量的影响更显著。

图9(c)为收发端仰角同时变化时信道容量的仿真结果。仿真条件为：tθ以20°的步长从10°增加到90°，rθ以20°的步长从10°增加到70°，其他仿真参数如表1和表2所示。由图9(c)可知，当tθ和rθ均大于40°时，信道容量最小；当tθ和rθ中至少有一个大于40°时，tθ和rθ的变化对系统信道容量影响很小，系统信道容量几乎为恒值，约为105bit/s；当tθ和rθ均小于40°时，系统信道容量较大。

4.3.2 发散角和视场角对系统信道容量的影响

发散角和视场角对系统信道容量的影响如图 10所示。图10(a)的仿真条件为：tθ和rθ均为45°，tφ以5°的步长5°增加到20°，d以20 m的步长从20 m增加到200 m，其他仿真参数如表1和表2所示。由图10(a)可知，信道容量随着tφ的增加变化较小；当tφ＜rφ时，tφ对信道容量的影响更小；当tφ＞rφ时，信道容量随着tφ的增加而略微减小，原因是发射光锥大于接收光锥，T发射的光子有少量未进入接收光锥，因此R接收到的光子数变少，引起系统的路径损耗增大、信噪比减小，进而导致系统信道容量减小。

图9 收发端仰角对系统信道容量的影响

图10(b)为视场角半角与系统信道容量的关系。仿真条件为：tθ和rθ均为45°，rφ以5°的步长从5°增加到20°，d以20 m的步长从20 m增加到200 m，其他仿真参数如表1和表2所示。由图10(b)可知，信道容量随着rφ的增大而逐渐增大；由仿真条件可知，tφ始终小于rφ，则发射光锥始终小于接收光锥；随着rφ的增大，公共散射体V增大，则接收端接收到光子的概率增大、脉冲展宽增大、路径损耗和系统带宽减小、信噪比增大。由香农公式可知，相比系统带宽，信噪比对信道容量的影响更显著，因此系统信道容量随着rφ的增大而增大。

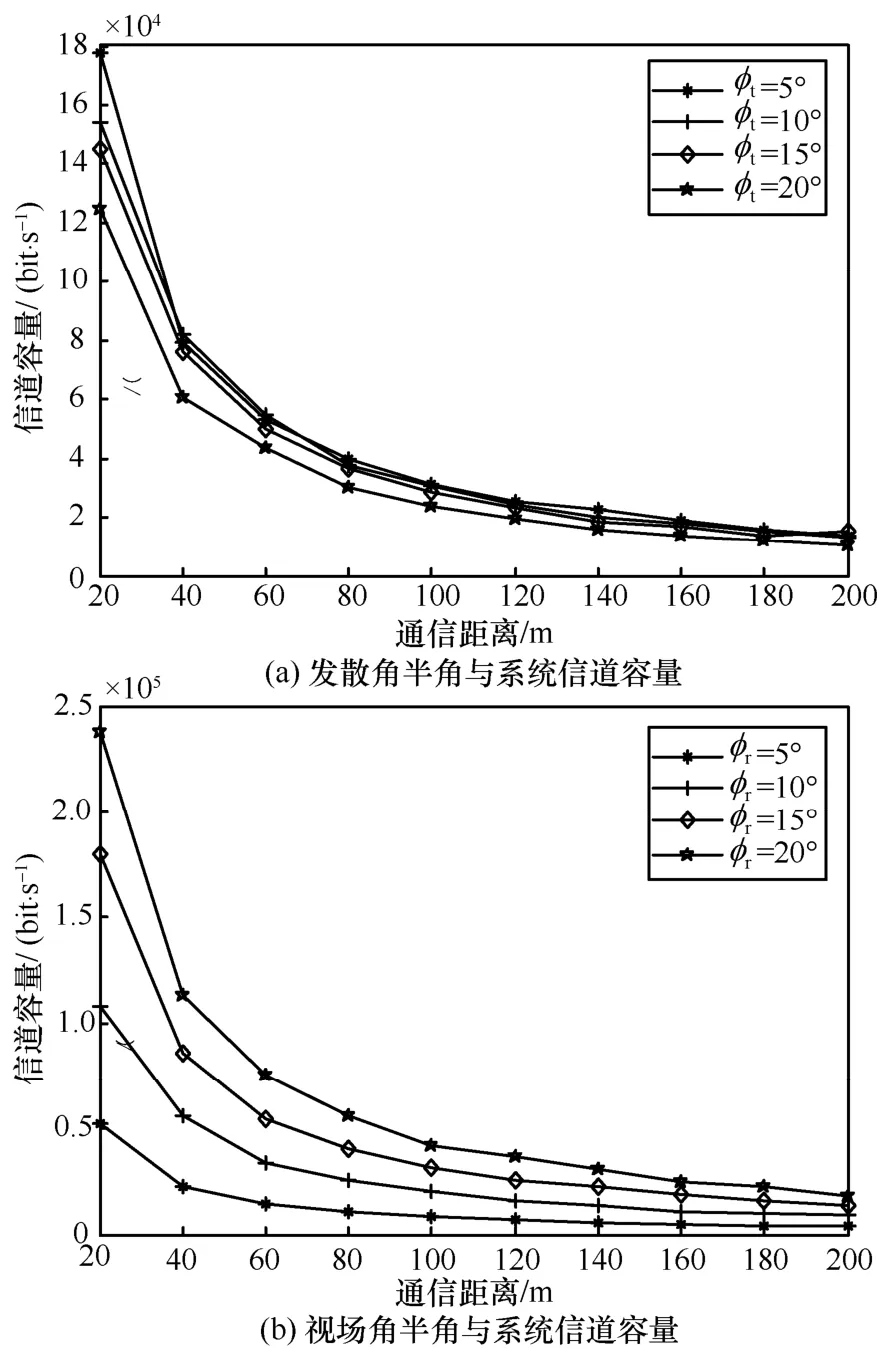
图10 发散角和视场角对系统信道容量的影响

4.3.3 接收端偏轴角对系统信道容量的影响

接收端偏轴角对系统信道容量的影响如图 11所示。仿真条件为：tθ和rθ均为45°，rα以5°的步长从5°增加到25°，d以20 m的步长从20 m增加到200 m，其他仿真参数如表1和表2所示。由图11可知，系统信道容量随着rα的增大而逐渐减小。当rα＜15°时，系统信道容量随着rα的增加而缓慢减小，当rα＞15°时，系统信道容量随着rα的增大而快速减小。原因是rα的增大将导致公共散射体V减小，进而使路径损耗增大和信噪比减小。由文献[25]的研究结论可知，rα的增大将会使系统的脉冲响应展宽增大、系统带宽减小；根据香农公式可知，信噪比和系统带宽的同时减小将会使信道容量变小，因此系统信道容量随着rα的增大而减小。

图11 收端偏轴角对系统信道容量的影响

5 结束语

本文基于高精度、简便运算的遍历微小单元法研究了非共面情况下紫外光通信系统的信道容量。仿真分析了系统带宽与通信距离，信道容量与发射端仰角、接收端仰角、发散角、视场角、偏轴角、通信距离之间的关系。结果表明：1)系统带宽随着通信距离的增大而逐渐减小，且减小的速率也逐渐减小；2)信道容量随着发射端仰角与接收端仰角的增大而减小，当发射端仰角和接收端仰角均较小时，相比接收端仰角，发射端仰角的变化对系统信道容量的影响更显著，当发射端仰角和接收端仰角均小于40°时，系统信道容量较大；3) 信道容量随着视场角的增大而增大，而信道容量随着发散角的增大而略微减小；4)信道容量随着偏轴角的增大而减小。下一步，计划对运动中的紫外光通信系统信道传输特性和链路间干扰展开研究。