基于相空间对称Lorenz阵子群的混沌保密通信研究

刘林芳，芮国胜，张洋，吴前龙

（海军航空大学信号与信息处理山东省重点实验室，山东 烟台 264001）

1 引言

混沌运动是自然界中存在的一类复杂的非线性运动，具有初值敏感性、有界性、类随机性、连续宽带频谱等特征[1-4]，因此在保密通信、信号检测、自动控制等诸多领域获得了广泛的应用[5-8]。早在1990年，数学家Pecora等[9]就提出了基于混沌理论的加密方法。混沌同步的理论和方法出现后，混沌保密通信便成为保密通信领域研究的热点，其研究主要集中于混沌同步控制、混沌加密算法等方面。

目前，国内外已提出的混沌同步控制方法有线性反馈法[10]、自适应控制法[11]、主动控制法[12]、非线性控制法[13-14]、滑模控制法[15]等。文献[16]研究了混沌系统与超混沌系统的脉冲同步，文献[17]实现了超混沌系统的完全同步及时延同步，文献[18]实现了不确定分数阶混沌系统的自适应神经网络同步控制。混沌保密通信主要有混沌掩盖通信[19]、混沌键控通信[20]、混沌调制通信[21]等。混沌掩盖通信的原理是在发送端将待发送信息隐藏在混沌系统所产生的混沌信号中，在接收端通过混沌同步去掉接收信号中的混沌信号，实现对原始信息的恢复。混沌键控通信的原理是在发送端利用2种不同的混沌信号分别代表0和1，接收端由与发送端相同的2个混沌阵子组成，通过判断每个码元内接收信息与混沌阵子的同步与否来解调出有用信息。混沌调制通信的原理是在发送端将待发送信息调制到混沌系统参数中，在接收端通过混沌系统的同步来恢复出混沌系统的参数，从而解调出有用信息。为满足混沌阵子在大规模通信中的应用需求，文献[22]研究了新的六阶混沌电路，文献[23]在现有混沌阵子的基础上构建了混沌阵子的沿坐标轴转动的模型。

综上，目前的混沌保密通信主要是基于混沌同步理论，利用混沌阵子的类随机性、不可预测性实现保密通信。虽然混沌阵子具有优良的特性，但是现有的混沌阵子数目有限、结构已知，且在大规模并发式混沌保密通信中需要用到大量的混沌阵子，针对这些问题，本文进行了以下研究：1)建立了混沌阵子的相空间对称模型，可由某一个混沌阵子得到混沌阵子群，阵子群中包含数目众多的对称阵子，能满足大量使用的需求；2)研究了阵子群的同步特性，得到了相空间对称阵子群的同步条件；3)设计了基于相空间对称混沌阵子的保密通信系统并对其进行理论分析和仿真验证，结果表明该方法具有较好的保密性能。

2 混沌阵子相空间对称模型

Lorenz混沌系统状态方程为

其中，x˙1为x1的一阶导数，b σ、γ、为系统参数，当时，系统进入混沌状态，本文以 Lorenz混沌阵子为例进行研究，其结论可应用于任意混沌系统。

2.1 理论模型

记三维空间直线l的参数方程为

记混沌系统方程为

定义1将式(3)的混沌系统相空间中任意一点x关于相空间中任意直线l对称的点记为点y，所有的关于直线l对称的点组成的系统称为混沌阵子相空间中关于直线l的对称系统，所有的对称系统组成混沌系统的相空间对称系统群。

由定义1可知，相空间对称系统的相轨迹仅仅在相空间发生了位置变化，其相轨迹图的形态、系统特性并未发生改变。以Lorenz系统为例，其系统相图和关于任意直线l1对称的系统相图如图 1所示。其中，直线l1的参数式方程为

图1 Lorenz系统相图及其关于直线l1对称的系统相图

混沌理论应用于保密通信主要是利用了混沌阵子处于混沌状态时信号的类随机特性，并通过混沌同步来解调信号。Lyapunov指数是判断混沌系统状态的重要参数之一，若最大Lyapunov指数大于0则可以判断系统处于混沌状态。通过计算可得，Lorenz系统关于直线l1的对称系统的最大Lyapunov指数为0.885 0，这验证了对称后的系统仍处于混沌状态，保持了混沌系统的优良特性。

2.2 相空间对称系统群的同步

定义2混沌系统(1)关于相空间中直线lm对称的系统表达式为

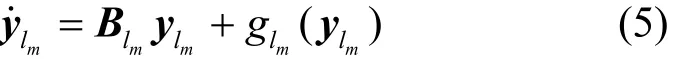
令相空间对称系统(5)为驱动系统，原系统(1)为响应系统，则有

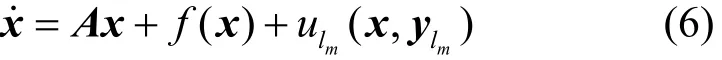
定义3若存在同步控制器，使式(7)中误差满足

则称原系统(1)与空间对称系统(5)达到同步。

定理1存在同步控制器

使驱动系统与响应达到同步，其中，Δ为n×n维正定矩阵。

证明由式(5)～式(7)和式(9)可知

因此有

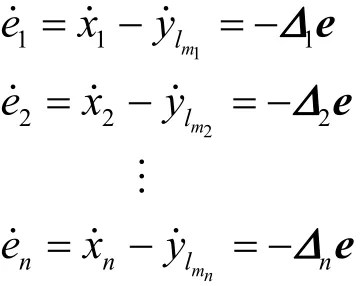
其中，Δn为1×n维矩阵。构造Lyapunov函数为，则有

因为Δ为正定矩阵，故有

由Lyapunov稳定性定理可得该系统渐进稳定，即存在同步控制器

使原系统与混沌相空间对称系统达到同步。

2.3 仿真验证

根据定义1，求得Lorenz系统关于直线l2、l3的相空间对称系统的方程分别为

根据式(1)、式(10)、式(11)及定理 1设计同步控制器，选取Δ为三维单位矩阵，符合定理1的约束条件，即则同步控制器为

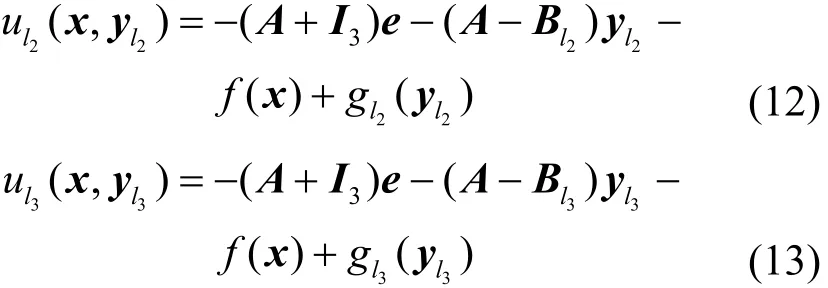
任选系统(10)初始值为(1,-3,4)，系统(11)初始值为(-2,3,5)。根据上述条件进行仿真，得到2个相空间对称系统相图及同步误差分别如图2和图3所示。从图2(a)和图3(a)可以看出，对称系统相图仍保持了Lorenz阵子的相图特性，但空间位置发生了变化；从图2(b)和图3(b)可以看出，在同步控制器作用下，驱动系统5 s后与响应系统完全同步。

3 基于相空间对称阵子群的混沌掩盖保密通信

混沌保密通信主要有混沌掩盖通信、混沌键控通信、混沌调制通信[19-21]，利用第2节提出的相空间对称混沌阵子群的混沌特性及同步特性设计混沌保密通信系统。本文仅设计了基于相空间对称阵子群的混沌掩盖保密通信模型，但是该对称阵子群也可应用于其他混沌保密通信模型中。

3.1 系统模型

基于相空间对称混沌阵子群的保密通信模型如图4所示。发送端首先在相空间对称混沌阵子群中选择某一对称阵子，利用该对称阵子产生信号的随机特性生成加密函数g(y)，再利用函数g(y)对待传输信号进行混沌掩盖；接收端在混沌同步控制器的控制下产生与发送端对称混沌阵子同步的信号，在此基础上生成解密函数h(x)，利用解密函数h(x)对接收到的信号进行解密得到有用信号。加密函数g(y)、解密函数h(x)的计算式分别为

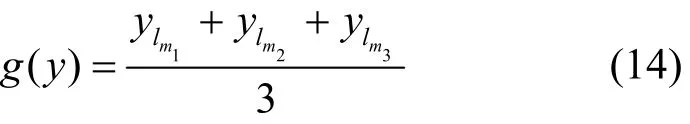
图2 相空间对称系统yl2相图及同步误差

图3 相空间对称系统yl3相图及同步误差

图4 基于相空间对称混沌阵子群的保密通信模型

采用混沌掩盖的方式对待发送信号m(t)进行加密，加密后的信号记为s(t)，加密算法如式(16)所示，其中k为比例系数，调节待加密信号幅度，一般使待加密信号幅度小于混沌信号幅度的以达到混沌掩盖的效果。接收端的解密算法如式(17)所示，解调出的信号记为m′(t)。

现有的基于Lorenz混沌阵子的混沌保密通信中的密钥主要为 Lorenz阵子的初始值和计算步长，在本文方法中，密钥除了Lorenz系统初始值及计算步长外，还包括阵子对称时的直线方程参数：点(x0,y0,z0)和方向向量。由于对称后的 Lorenz阵子仍处于混沌状态，具有混沌系统的初值敏感性，因此本文方法在不降低现有方法性能的基础上密钥空间更大，保密性更强。

3.2 仿真验证

利用相空间对称阵子对常用的正弦信号进行加密传输验证实验，根据图4的传输模型，分别设计2个实验。

2) 利用式(11)的对称阵子加密信号m2(t)=sin2t后进行传输，接收端经过同步后解密出原始信号。

其余参数与2.3节和3.1节相同，信号m1(t)和m2(t)加密传输的仿真结果分别如图5和图6所示。

从图5(a)和图 6(a)可以看出，待传输信号经过加密后完全被掩盖在混沌信号中，达到了混沌掩盖保密通信的效果；从图5(b)和图6(b)可以看出，接收端在5 s内迅速达到混沌同步，经过混沌同步后正确解密出了原始信号。

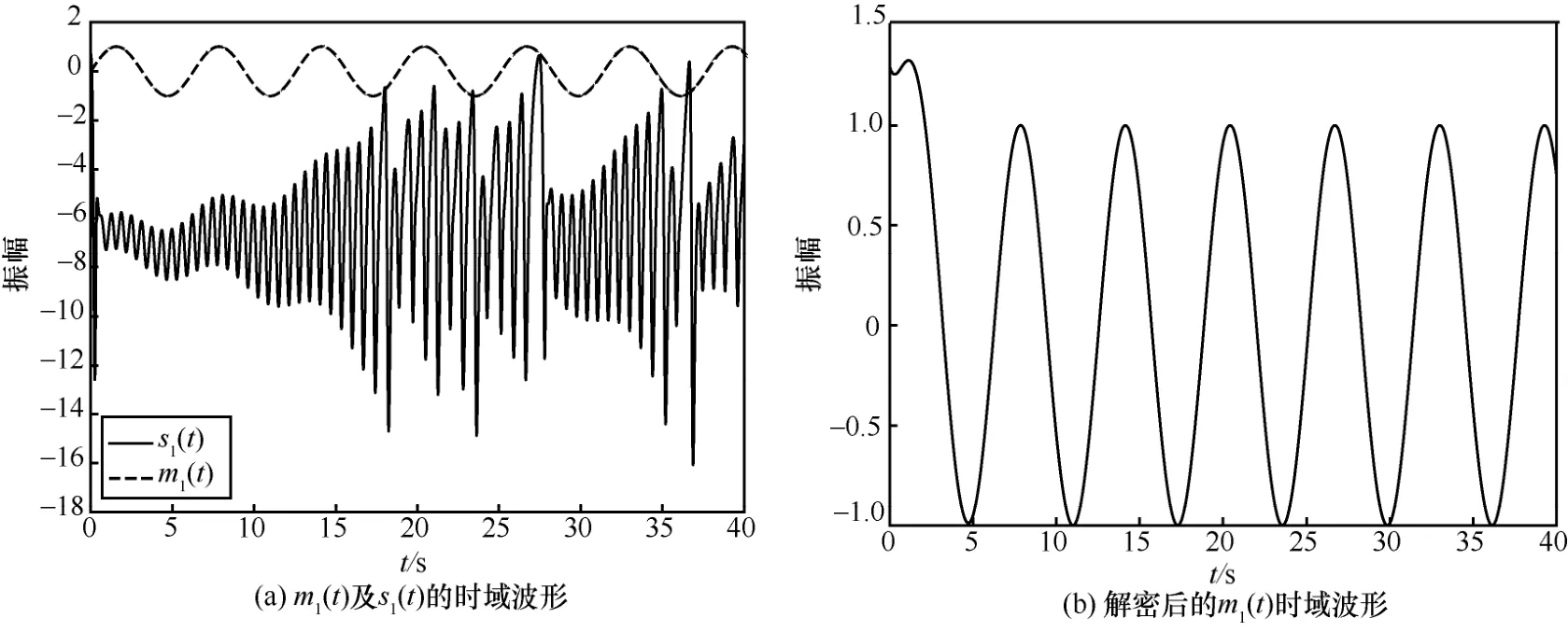
图5 信号m1( t)传输实验时域波形

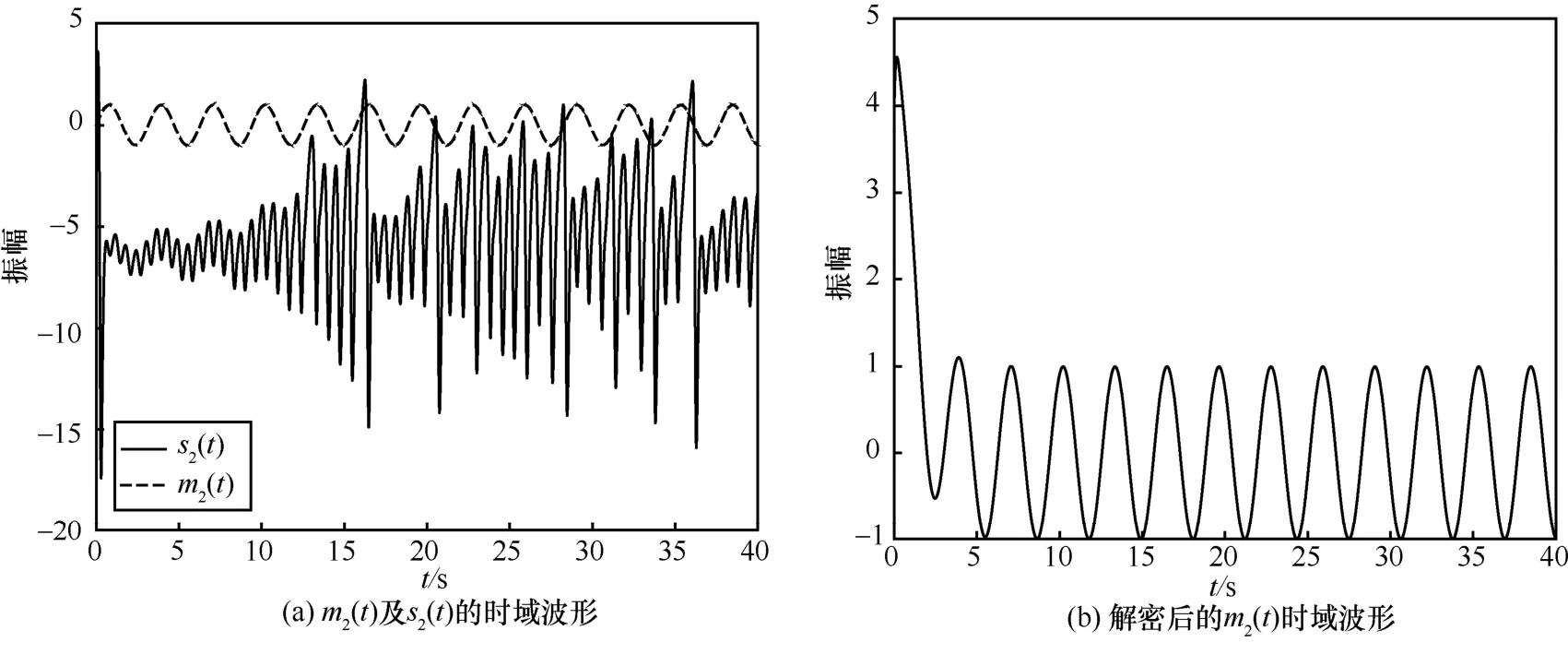
图6 信号m2( t)传输实验时域波形

在图4的传输模型中，每次发送信号时选用不同的对称阵子进行加密，假设窃听者窃取了传输信号m1(t)时所用的对称混沌阵子式(10)的信息，并利用该信息解密信号m2(t)，其结果如图7所示。从图7可以看出，窃听者并不能利用该信息正确解密出信号m2(t)，因为每个对称混沌阵子在相空间的位置各不相同，即便窃取了某一对称阵子的信息也无法解密出由其他对称阵子加密的信号。

图7 对称阵子yl2解密信号m2( t)的时域波形

综上可知，本文方法具有以下优点：空间对称混沌阵子群理论上包含无数多个对称阵子，可对不同的信号采用不同的对称阵子进行加密，且各阵子只能解密自己加密的信号，具有较好的保密性；同时，与使用大量不同种类混沌阵子进行保密通信的方法相比，本文方法在不降低保密性能的前提下降低了实现的复杂度，实用性更强。

4 结束语

本文首先研究了混沌阵子相空间对称模型，该模型中对称阵子既能保持原有的混沌特性，又能提供大量可用于保密通信的对称阵子；然后研究了相空间对称阵子群的同步问题，实现了对称阵子系统与原系统的同步；最后在同步的基础上提出了基于相空间对称阵子群的保密通信模型，并对其进行仿真验证。仿真结果表明，本文方法能有效实现混沌掩盖保密通信，具有较好的应用前景。数目众多的对称阵子可在多信道并发通信中使用，在与MIMO等其他技术相结合发挥其保密功能方面也具有较好的应用前景。