一种改进的MSK信号解调算法*

张 辉，代遵超

（中国电子科技集团公司第三十研究所，四川 成都 610041）

0 引 言

最小频移键控（Minimum Frequency Shift Keying， MSK）调制方式具有恒定包络、频带利用率高、带外辐射小、抗干扰能力强等特点，在无线通信尤其是军用通信系统中得到广泛应用。对于MSK调制方法，一般都是将MSK看成是一种特殊的频移键控（Frequency Shift Keying，FSK）信号进行数字化解调[1]。但是由于MSK信号的调制指数很小，信号载频很难分离，使得最终解调效果较差[2]。本文提出了一种频域的MSK解调算法，对载波频偏和相移不敏感，与传统解调方式相比能获得更优解调性能，且算法复杂度低，具有较强可实现性。

1 MSK常用解调方法

MSK是连续相位频移键控（Coutinuous-Phase Frequency Shift Keying，CPFSK）中调制指数为0.5的特例，是二进制频移键控（2FSK）的改进型，相比于2FSK信号码元变化时在2个频率之间瞬时切换，导致码元变化时相位不连续，MSK具有连续相位，包络恒定，信号波形无突然跳变。MSK信号的频率偏移为±1/(4Ts)，Ts为1个码元周期，即频偏是码速率的1/4，相应调制指数h=1/2。

MSK的信号波形可以用下式来表示：

式中，fc是载波频率，dk=±1表示双极性码元数据，Ts表示一个码元周期，φk=nπ是在第k个二进制数据持续时间的相位常数。

由MSK信号调制表达式可见，其通过键控方式改变载波频率，因此与ASK（Amplitudeshift Keying，幅移键控）、FSK、PSK（Phase-shift Keying，相移键控）类数字调制相同，其解调方式也分为相干解调和非相干解调两类方法。

相干解调根据MSK特点分为利用两组频移载波或利用中间载波的相干解调方法，由于两种方法都要求获取准确的载波频率和相位信息，要求利用锁相环路实现载波跟踪，因此主要适用于连续波MSK信号解调，针对短时突发MSK信号由于跟踪时间有限导致载波频率精度不足，对解调性能有较大影响。

MSK信号非相干解调典型的方法有包络检波方、鉴频法、差分检测法、过零检测法、延迟判决相干解调法等，在低信噪比条件下相干解调法的性能优于非相干解调法，然而非相干解调不需要相干载波，因而算法实现比较简单[1]。

此外也有文献提出，可采用离散傅里叶变换（Discrete Fourier Transformation，DFT）方法进行解调[3]，即在一个完整的码元周期内分别对fc±1/(4TS)两组频偏利用DFT变化进行时频转换，并求出对应频率偏移的幅值，最后通过比较两组幅值大小即可完成解调判决，但该方法在DFT计算前需要预先获知比特同步信息。

上述方法各有优缺点。本文针对高速率、频率频偏未知、码元未同步的MSK信号，提出了一种改进的DFT变换MSK解调方式，具有解调性能优、实现复杂度低的优点。

2 改进的DFT变换MSK解调算法

根据MSK信号表示式（1）可得出，MSK一个码元内的信号实际是一个单载波信号，载波的频率根据码元信息不同分别为fc±1/(4TS)，因此MSK信号的表达式可改写成：

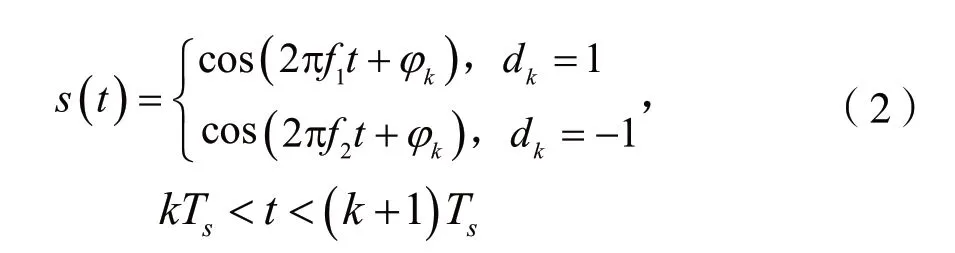
式中，f1=fc+1/(4TS)，f2=fc-1/(4TS)。

由式（2）可见，在一个码元周期内，MSK信号的基带信息+1表征的f1与基带信息-1表征的f2是正交的。因此，在码元同步基础上，对某一个码元的解调可转换为在kTs＜t＜(k+1)Ts时段内对f1和f2两个频率分量幅度的比较。

解调原理框图如图1所示。

图1 DFT变换MSK调原理框

解调处理过程利用DFT运算对一个码元周期内信号做时频域变换后，f1和f2两个频率分量的信号表达式如下：

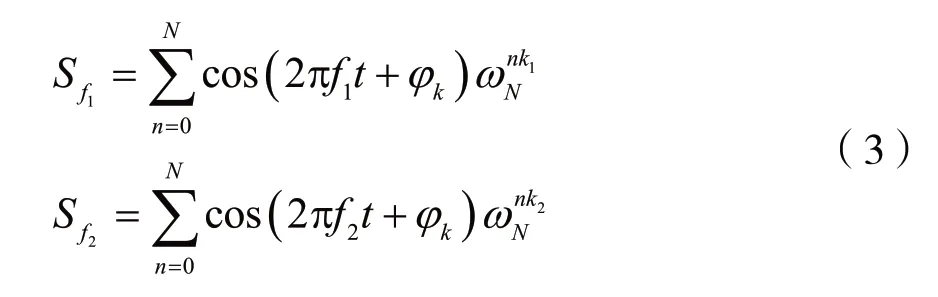
式中，ωN=e(-2πj)/N，k1、k2分别为f1和f2两个频率分量对应的DFT变换谱线，t=1,2,…,m为一个码元周期内采样点数。解调处理通过比对两个频率分量模值，如则dk=+1，反之dk=-1。

考虑在实际段时突发MSK通信中，难以在DFT变换前做到码元同步，因此本文在时频域转换中引入Goertzel算法[4]，利用Goertzel算法在有限频率点计算简洁、高效的优点，在码元同步前进行短时傅里叶变换，在保证时间分辨率的条件下获取MSK信号两个频率分量的频域信息，两组频域分量求模做差后获取基带波形，最后抽样判决恢复码元信息。

改进后的MSK解调原理框图如图2所示。傅里叶变换由下式定义[5]：

图2 MSK频域解调原理框

其中，ωN=e(-2πj)/N。由式（3）展开可得：

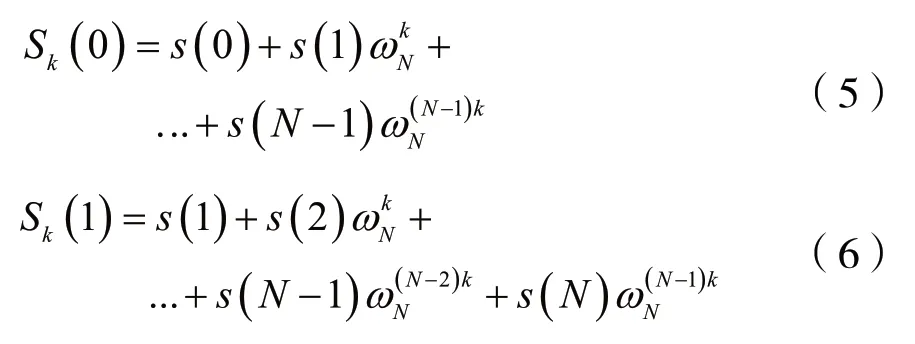
通过式（5）、式（6）推导可得，Goertzel算法的递归算法结构如下：

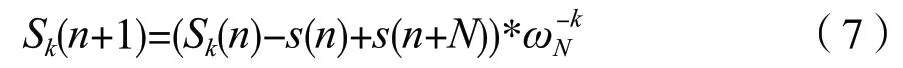
上式表征了信号在频率分量k上N点DFT变换结果随时间变换趋势。

根据MSK信号的特点，可知在码元周期dk=1时，其f1频率分量上得到的DFT变换幅值必然大于f2频率分量上的DFT变换幅值，反之亦然，因此通过对f1和f2两路频率分量上DFT变换幅值结果作差，可得到去除载波后的基带频移键控信息，频域的基带波形表达式如下：

最后利用基带波形完成抽样判决后即可恢复出二进制码元。解调过程中各环节信号波形分别如 图3所示。

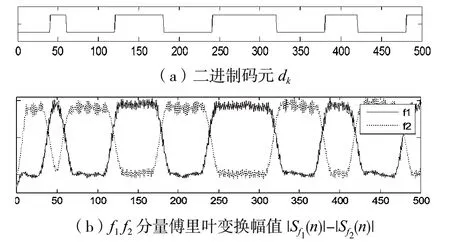
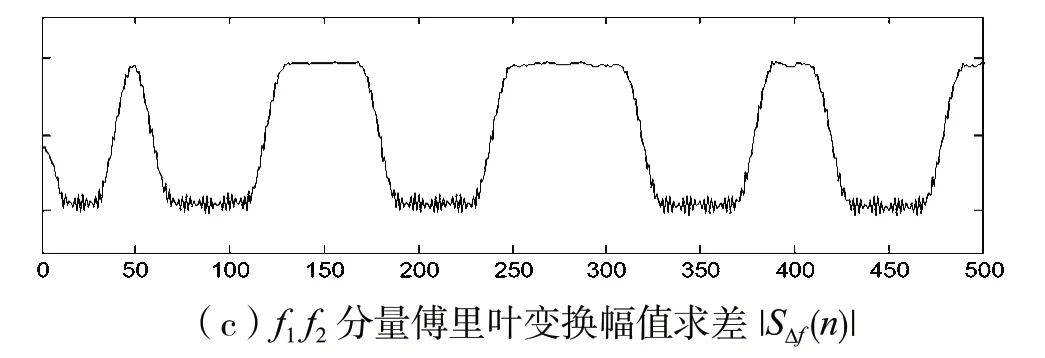
图3 解调各环节信号波形

3 计算机仿真与分析

算法仿真流程为：二进制信源—MSK调制—叠加噪声—MSK解调—二进制信源恢复—误码率统计。以敌我识别系统Mark XIIA Mode 5中使用的MSK信号参数为基础建立仿真模型，MSK码速率为16 Mbit/s。其他参数设置包括：载频fc=10 MHz， 采样率fs=40 MHz。MSK信号两个频率分量分别为f1=14 MHz、f2=6 MHz，考虑采样率以及两个频率分量间隔，Goertzel时频变换DFT点数N取10，即频率分辨率为4 MHz，通过计算两组频率谱线就可完成解调算法。图4为在不同信噪比条件下，本文算法与相干解调法、延迟判决解调法误码率蒙特卡洛仿真结果。

图4 本算法与其他解调算法误码统计

由图4可见，改进的算法误码性能明显优于MSK解调广泛使用的延迟判决算法，略差于相干解调法。但由于相干解调法算法需要从接收信号提取出相干载波，实现结构比较复杂，且在载波频率未精确对准情况下，解调性能误码性能将显著恶化。而本文提出算法利用DFT计算频域能量来提取解调信息，因此对频偏不敏感，在存在频率偏移情况下的解调误码性能明显优于相干解调。

图5为信噪比12dB时存在不同频偏情况下两种算法解调误码性能统计，在频率偏移超过基带码速率0.5%后改进算法出现误码，但此时的误码性能仍优于相干解调算法约2～3个数量级。

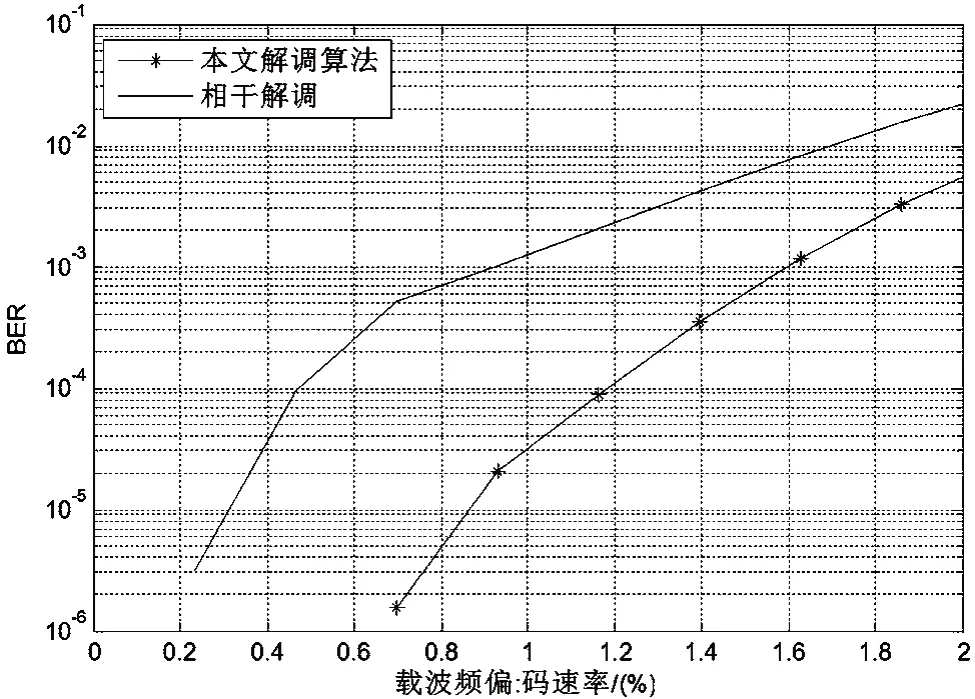
图5 频偏条件下算法与相干解调误码统计

4 结 语

本文结合Goertzel算法提出了一种改进的基于DFT变换的MSK解调算法，该方法解决了DFT变换的MSK解调需要先获取MSK码元精确同步的问题，通过仿真计算分析表明，解调算法还具有对误码性能好、载波频偏不敏感等优点，同时算法采用递归结构，计算量小，实现简单、高效，适合在对短时突发MSK信号非合作解调等场合应用。