窄带电力线载波通信信号识别算法研究*
2019-06-10赵红军王永建
李 坤,赵红军 ,2 ,王永建
(1.绵阳职业技术学院 信息工程系,四川 绵阳 621010;2.西南科技大学,四川 绵阳 621000; 3.国家计算机网络与信息安全管理中心,北京 100031)
0 引 言
电力线通信分为窄带通信(NB-PLC,3~ 500 kHz)和宽带通信(BB-PLC,1.8~250 MHz)。 窄带通信在智能电表中的应用比较广泛,而宽带通信则应用在家庭电力网中,可以提供几百兆比特每秒的高速数据传输。电信工业协会-1113和国际电信联盟(ITU-T)已经制定了电力线通信的一些标准,如IEEE P1901和ITU-TG.hn[1]。
电力线载波通信信号的识别已经成为该领域的一个研究方向。因为电力线信道具有强噪声干扰、衰减和多径效应[1],所以在接收端获得一个理想的调制信号非常困难。当前,对调制信号的识别已经成为电力线通信必须解决的难题。
信号调制模式识别算法主要有两类:基于统计模式的识别方法[2]和基于检测理论的识别方法[3]。由于检测理论方法计算复杂、识别信号种类较少且信号的似然函数只能在高斯白噪声环境下求得,所以该方法不适用在电力线信道中。目前,调制方式识别算法的主要研究方向是将统计识别方法和神经网络方法相结合,在选取合理的特征值和神经网络算法的前提下,以达到较好的识别效果。
在数字信号自动识别研究中,Nandi和Azzouz做出了巨大贡献[2,4]。他们使用决策理论方法和神经网络方法成功识别了2ASK、4ASK、2PSK、4PSK、2FSK和4FSK信号。Diego Alves Amoedo等人[5]使用支持向量机方法成功识别AM、FM、BPSK、QPSK、16QAM、64QAM和GMSK信号,但是识别效果不是很理想。Husam Alzaq等人[6]使用神经网络方法成功识别了MASK、MPSK和MFSK信号,但是神经网络存在过学习、欠学习问题,会对识别效果造成一定影响。Salman Hassanpour[7]使用小波变换方法成功识别出DPSK、PSK和MSK;Alharbi Hazza等人[8]提出基于特征的方法,成功识别出FSK、ASK、PSK和QAM等信号,但是其所设计的识别装置计算复杂。Liedtke[9]使用统计模式和决策理论方法成功识别了AM、2ASK、2PSK、4PSK和2FSK信号,但是该识别器的实现比较复杂,且信噪比大于18 dB时才能实现无错识别。文献[9-11]通过使用小波特征作为支持向量机的特征元素对信号进行识别。文献[12]使用连续小波变换的高阶统计矩阵作为特征集,采用向前神经网络作为识别器。目的是区分不同的多位移键控信号。
以上文献所使用的方法大部分是在高斯白噪声情况下完成信号识别,而本文考虑到PLC信道的实际情况,且在识别率和识别信号种类上都有所体现。在PLC信号识别方面,本文采用统计模式识别方法,并设计了一种改进的基于支持向量机的调制信号识别器。首先获取信号的高阶累积量,其次对其进行小波变换处理,并提取特征参数,最后将两类特征参数输入到改进的支持向量机中识别信号类型。在近似电力线信道环境下,仿真结果表明该方法能得到较好的效果。
1 信号和信道模型
1.1 信号模型
调制信号经过电力线通信信道后,假设接收信号的载波是完整的,频率和相位同步,那么调制信号的基带表达式可以定义为[13]:
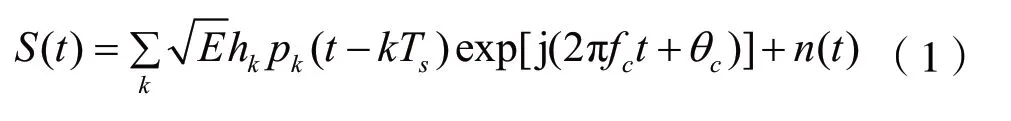
其中k=1,2,…,N,N是发送码元序列的长度,hk是发送码元序列,p(t)是发送码元的波形,Ts是码元宽度,E是信号能量,fc是载波频率,θc是载波相位,n(t)是电力线信道噪声[14-15]。
根据调制信号的特性,经过降频转换后,MASK、MFSK、MPSK和MQAM表达式如下[16]:

其中ak∈{2m-1-M | m=1,2,…,M}。
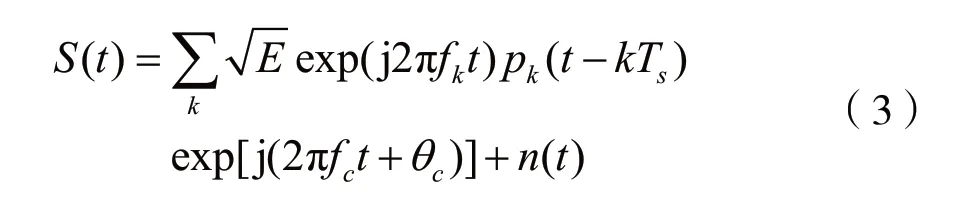
其中fk∈{(2m-1-M)Δf | m=1,2,…,M},Δf是频率偏移。
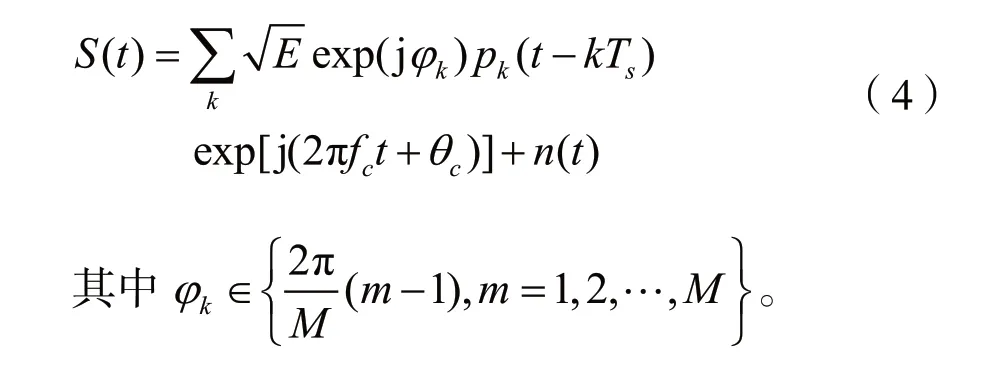
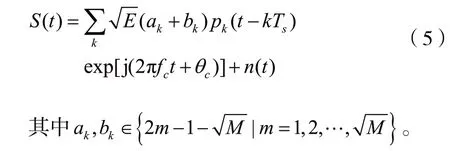
1.2 信道模型
1.2.1 背景噪声模型
实际电力线的噪声包括两部分:背景噪声和脉冲噪声[14,17]。本文的背景噪声采用概率密度服从Nakagami-m分布的模型表示[15,18-19]。文献[20]验证了该噪声模型是可行的。背景噪声的特征向量X服从Nakagami-m分布,概率密度函数为:

其中,Γ(*)是伽马函数,Ω是背景噪声的平均功率,定义为Ω=E[X2],这里E[*]表示期望,m是Nakagami-m的参数即形状因子,表示衰减的严重程度。m=E[X2]/E[(X2-E[X2])2]≥0.5。
1.2.2 脉冲噪声模型
在单位脉冲函数imp(t)的作用下,可以得到电力线信道下的脉冲噪声模型nimp:
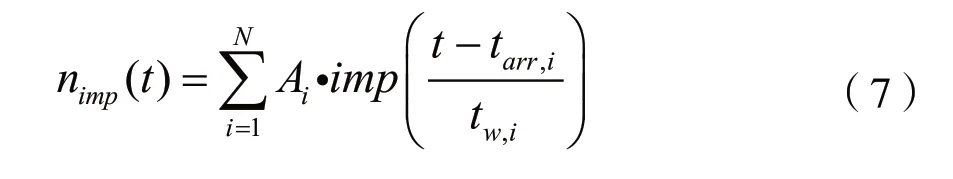
其中参数Ai表示第i个脉冲噪声的幅度;tw,i表示第i个噪声持续时间,即噪声宽度;tarr,i表示第i个噪声产生时刻。Ai、tw,i、tarr,i三个参数取值是随机的,具体取值可参考文献[21]。
2 特征提取
2.1 高阶累积量的计算
假设k阶实的平稳随机过程x(t)是零均值的,则它的k阶累积量计算式为[22]:
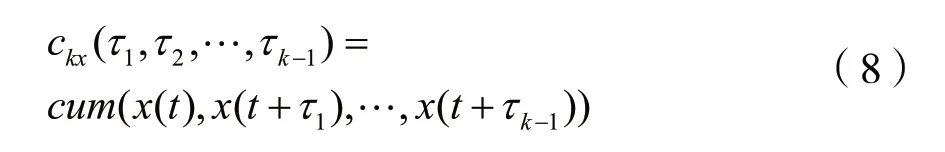
接收到的信号可以表示为r(t)=s(t)+n(t),s(t)表示发送信号,n(t)表示电力线信道噪声,即背景噪声和随机脉冲噪声,且s(t)和n(t)是独立的。根据累积量的特性,可以得到等式:

在对接收信号进行高阶累积量处理前,先用小波去噪方法对信号进行处理,可以去除部分背景噪声和脉冲噪声,再通过高阶累积量的计算得到式(9)的近似等式[23]:

由式(10)知,在电力线噪声影响下,计算信号的高阶累积量值,同样可以识别信号调制模式。在理想信道下,假如发送的码元是独立同分布的,且信号的能量为E,每一阶累积量的理论值如表1所示。

表1 各阶累积量的理论值
2.2 特征参数提取
表1给出了部分信号的高阶累积量的值。但是,用累积量的方法无法识别2ASK和2PSK信号以及MFSK和8PSK信号。通过文献[24]了解到,MFSK信号经过求导后具有幅度调制特性。所以,计算MFSK信号的导数的高阶累积量,可以识别MFSK信号。

为消除冲击函数的影响,对式(11)进行中值滤波处理后得到:
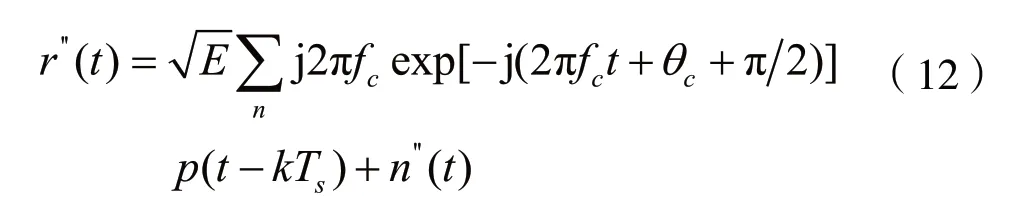
经过求导和中值滤波后,n"(t)仍然是电力线信道噪声。对式(12)进行Haar小波去噪处理,然后在表2中给出MFSK信号的二阶导数的累积量值。

表2 r"(t)的各阶累积量
根据表1和表2,本文设计了一种抗噪声性能较好的信号识别特征参数,具体表示形式如下:

其中,f1、f2、f3和f4是根据表1的结果计算出来的特征值,f5是根据表2的结果得出MFSK信号的特征值。计算后的特征参量如表3所示。
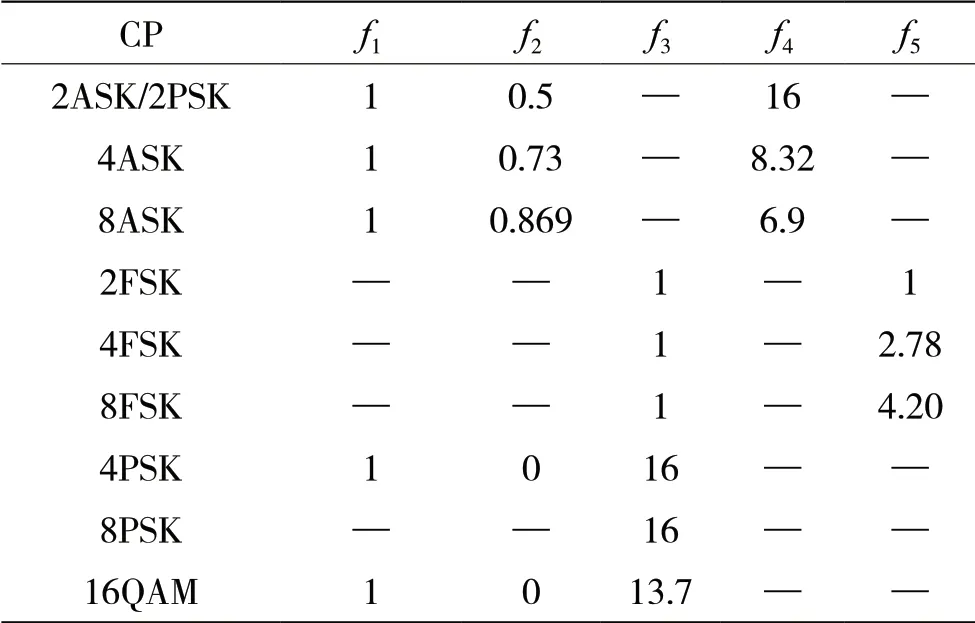
表3 提取的特征值
通过式(13)描述的方法,仍然无法识别2ASK和2PSK信号。根据文献[25],2ASK和2FSK信号的小波变换幅值方差具有明显差异,所以本文对这两种信号进行Haar小波变换,然后求出其幅值方差,从而确定判决门限f6的大小。这两种信号可以直接根据f6进行判决,不需要经过支持向量机,减少了识别的复杂度。
3 识别器设计
SVM可以实现两类信号的识别,但是当需要识别多种信号时,要使用扩展的SVM[26-27]。文献[27]采用1-VS-R(One-vs-Rest)SVM分类算法,结构逻辑较为简单。m类信号需要使用m个支持向量机,但是每个支持向量机都需要使用所有样本进行训练。文献[28]采用有向无环图(Decision Directed Acyclic Graph,DDAG)SVM分类算法,在训练支持向量机方面比较简单,除最上层的支持向量机外,其他每个都只使用样本的一部分进行训练,但逻辑比较复杂,且需要的支持向量机的数量也较多。本文结合所求特征参数的特性,采用一种二叉树结构的支持向量机识别信号。二叉树结构判断逻辑较为简单,所用的支持向量机较少,而且训练样本也是逐级递减的[28]。本文所用的分类器结构如图1所示,其中特征参数f1~f5分别代表一个支持向量机,而判决门限f6可直接识别信号,故不需要支持向量机。

图1 数字调制信号识别流程
本文识别器的具体识别步骤如下:
(1)使用小波变换对接收信号进行去噪处理;
(2)计算信号的高阶累积量和2ASK、2FSK信号小波变换的幅值方差,并构建特征参数;
(3)将提取的特征参数构成特征向量作为BT-SVM分类器的输入;
(4)为SVM选择核函数,本文识别实验中选用了径向核函数。径向核函数可以将样本非线性地规划到更高维空间,从而解决类标签和属性间非线性的关系问题[29]。
(5)训练BT-SVM分类器,完成训练后对测试样本进行分类识别。
4 仿真和实验分析
我国窄带电力线载波频率使用范围为40~ 500 kHz,载波频带带宽为4 kHz。仿真参数设置如下:采样频率fs为600 kHz,载波频率fc为60 kHz,比特率Rs为1 200 b/s,频率偏移为2 kHz,符号数为600,载波幅度为1,信噪比范围在-5~20 dB,噪声为电力线信道噪声。每个信号分别进行600次独立实验,信号之间无相关性。通过式(13)提取特征参数,有400次实验结果作为训练样本,其他作为测试样本。在信噪比为-5~20 dB时,在所设计的分类器中,支持向量机使用的特征参数f1~f5和小波幅值方差实验仿真如图2所示。

图2 特征参数仿真曲线

如图2所示,图2(a)中特征参数f1用于识别{2ASK,2PSK,4ASK,8ASK,4PSK,16QAM}和{2FSK,4FSK,8FSK,8PSK};图2(b)的仿真曲线用于识别{2ASK,2PSK,4ASK,8ASK}和{4PSK,16QAM};图2(c)的仿真曲线可以识别4PSK和16QAM;图2(d)的仿真曲线可以识别{2FSK,4FSK,8FSK}和8PSK;图2(e)中特征参数f4用于识别2ASK、2PSK、4ASK和8ASK;图2(f)中特征参数f5可以识别2FSK、4FSK和8FSK;图2(g)中特征参数f6可以识别2ASK和2PSK。可见,本文所用到的方法具有较好的识别效果,同时具有很好的抗噪声性能。
在图1的识别器结构下,表4和表5给出了各调制信号的正确识别率,结果是600次独立试验后得到的一个平均值。

表4 信噪比为17 dB时,各调制方式正确识别率/(%)

表5 信噪比为17 dB时,MFSK信号正确识别率/(%)
为了说明本文识别器的有效性,在相同高斯白噪声条件下,本文识别器与同类识别器[29]做了对比,结果如图3所示。当信噪比为-2 dB时,文献[29]设计的识别器识别率为82%,而本文设计的识别器识别率可以达到87.1%。随着信噪比的增大,虽然两种算法的识别率没有明显差异,但是本文的识别装置可以识别更多种类信号,且训练的样本逐级减少,降低了运算的复杂度。
此外,本文采用BT-SVM分类器和前向神经网络分类器对电力线调制信号进行识别性能分析。信噪比在-5~20 dB的情况下,图4给出了两种分类器的识别率仿真曲线。可以看出,在小信噪比下,本文所改进的支持向量机识别器和前向神经网络识别器都具有很好的抗噪性能,但是在大信噪比情况下,由于前向神经网络存在欠学习和过学习的缺点,前向神经网络识别器无法达到很好的识别效果。
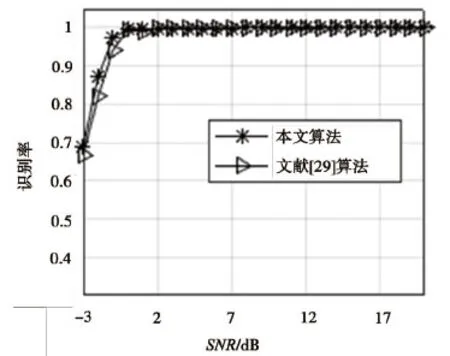
图3 本文与文献[29]对比结果

图4 两种算法的仿真曲线比较
5 结 语
本文针对电力线信道环境提出了一种改进的基于二叉树的支持向量机的调制信号识别方法,提取6个特征参数就可以很好的区分2ASK、4ASK、8ASK、2FSK、4FSK、8FSK、2PSK、4PSK、8PSK和16QAM信号。该识别器的识别算法相对比较简单。将电力线信号的高阶累积量作为信号识别的特征参数,并给出2ASK和2FSK信号的幅度方差的判决门限。这样在以二叉树结构的支持向量机分类器中,既避免了决策阈值的选取,同时也减少了支持向量机的数量。而且该识别器对于电力线噪声来说具有很好的鲁棒性。为了验证所提识别的性能,本文做了大量的仿真实验和对比实验。仿真结果表明,当信噪比为5dB时,前向神经网络分类器的识别率为81%,而本文所提出的识别器的识别率可以达到91%。达到这样的效果是因为在提取特征参量时高阶累积量和小波变换幅值方差都具有很好的抗噪声性能。由于减少了支持向量机的数量,该算法的计算量也相应的减少了。
