DVB-S2X接收系统定时同步算法的优化改进*
2019-06-10刘俊峰牛伟鹏王言匀
刘俊峰 ,李 刚 ,龙 军 ,牛伟鹏 ,王言匀
(1.中南大学 计算机学院,湖南 长沙 410075;2.湖南省军区,湖南 长沙 410010)
0 引 言
近年来,世界各国卫星通信技术发展迅速,我国在“逐梦太空”等项目中,对卫星通信的研究投入更大、更广、更深。美国相继提出了转型通信体系、空间通信与导航体系结构(SCaN)等计划;欧洲各国合作推出了多国天基成像系统、伽利略系统计划,预计在2020年左右投入运行[1]。蕴含着重大战略利益跨层、跨协议的空、天、地三体组成庞大的空间信息网络中[2],已经成为世界各国争相发展的重点。卫星通信作为其重要组成成分,具有传输远、覆盖广、通信不受地理条件限制等优点,在军事侦查、通信广播、应急救援、民生服务等领域有着广泛的应用[3-4]。今年全国两会召开,中央广播电视台首次采用5G+4K高清直播,说明人们已经迈向4K甚至8K超高清电视(Ultra High Definition Television,UHDTV)、互动电视等其他富媒体模式,这也推动卫星数字广播标准技术朝着安全抗干扰、移动化、更高频谱效率、更强健的服务能力方向发展[5]。因此在高新信息技术不断创新的潮流中,对卫星通信信息接收有了更高的要求。
2014年2月,DVB组织通过了最新的DVB-S2扩展版技术规范DVB-S2X[6]。DVB-S2X标准采用了更高效的信道编码、更多高阶调制技术、自适应(Adaptive Coding and Modulatin,ACM)技术等卫星数字传输技术,前向兼容DVB-S2标准,不仅能满足民用消费者观看电视节目的需求,而且能充分发挥卫星信道频带宽、传输信息量大、覆盖能力强、不受地域限制的优势,使得电视广播技术向着更高频谱效率、更大接入速率、更好移动性能、更强服务能力、更小成本方向发展[7]。
定时同步是在接收端提取时钟信号,周期采样进行处理,使得系统收发以相同的“步伐”进行,消除系统中存在的码间干扰(Inter-Symbol Interference,ISI)。定时恢复作为卫星通信接收系统中最关键的功能之一。卫星信号解调到基带后,为获得准确的采样值,需要使接收定时采样频率与信号周期发送频率一致。当收发双方不一致时,不仅会引入码间串扰(ISI),降低有用信噪比,也为后续载波同步建立带来困难。现有DVB-S2X结构采用Gardner定时同步算法,但在信噪比较低场景下定时会存在抖动,难以满足终端小型化趋势。
1 DVB-S2X接收系统定时同步模型
DVB-S2X卫星通信信息接收系统在存在高动态、相位抖动、电磁环境复杂、非线性失真等传输信道条件下,为能准确、高效接收到下行信号,满足高质量传输要求,就需要接收系统同步器件能够在环境恶劣条件下顺利完成符号定时同步、载波恢复同步和帧同步等同步恢复,从而能够在接收端可以顺利接收消息。
1.1 定时同步模型
卫星信号经过解调后,由带通信号变换为基带信号,在送入译码器前,首先要对定时、频率、相位等同步参数进行修正。这其中涉及到参数修正顺序问题。一般来说,定时同步未实现的前提下,载波的频率和相位估计性能较差;而定时算法对频偏和相偏并不敏感[8]。因此,在同步的实现顺序上,首先进行定时同步,即定时同步在匹配滤波器后首先进行。定时同步的基本模型如图1所示。
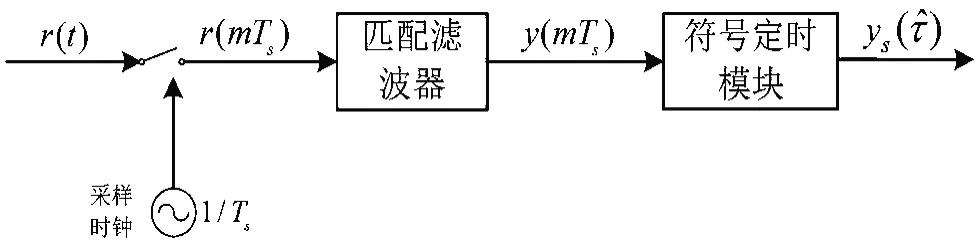
图1 定时同步模型示意图
1.2 Gardner定时同步环路基本原理
Gardner算法属于非数据辅助算法,采用反馈结构,其定时误差检测器只需要一个符号的两个采样值,实现复杂度低,且在存在载波偏差情况下仍能够工作,因而在实际系统中应用较广。
基于上述特点,DVB-S2X选用其用于实现定时同步。其算法实现框图如图2所示。
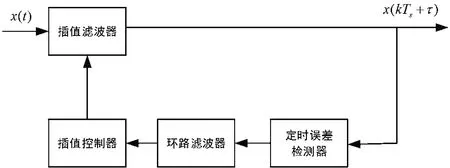
图2 Garnder算法实现框图
Gardner定时算法由插值滤波器、定时误差检测器、环路滤波器、插值控制器4个模块组成。其中,定时误差检测器用于输出一个与定时偏差成比例的检测量,环路滤波器用于将输出检测量进行滤波平滑,定时控制器完成对定时振荡器的调整,通过调整输出频率来实现跟踪,插值滤波器根据定时控制器输出,利用内插原理,插值输出最优值。
Gardner定时恢复算法因其对调制方式(从QPSK到32APSK)不敏感的非数据辅助算法,能够容忍一定的频偏,因而在DVB-S2X建议标准中被采用。由于篇幅有限,Gardner定时恢复算法在此不再详细推导。
2 基于编码辅助的改进DVB-S2X算法
DVB-S2X算法中定时同步算法采用了Gardner算法,但是Gardner算法有其固有缺陷,在低信噪比条件下,受限于环路参数设置窄,跟踪参数容易受影响,在同步跟踪过程中容易受到失锁,且从上述图中可以看出,Gardner定时算法跟踪完成后,仍会有残留抖动,这些均对后续译码的译码性能产生影响,在优化达到香农限的情况下还存在差距。图3给出了存在定时偏差情况下,低密度奇偶校验(Low-density Parity-check,LDPC)码译码性能,可以看到定时偏差的存在,导致误码率性能恶化。因此,在捕获阶段可以采用Gardner算法,但是在跟踪阶段需要采用可靠性高的定时同步算法。受限于有限导频长度,我们不在其帧头长度上进行改进,这样会降低系统效率,并对整个DVB-S2X结构产生较大变化。因此,传统的数据辅助算法并不能对同步的可靠性提出进一步改进。由于DVB-S2X采用了LDPC编码结构,信道编码使得编码比特间具有内联性,利用这种内联性,则可以用于辅助进行定时同步,即编码辅助同步算法。

图3 定时偏差对LDPC码译码性能影响
2.1 码辅助工作基本原理
现有文献研究中,码辅助同步算法按照译码器修改与否分为两种。一种是改造译码结构,将参数估计与译码过程相结合。文献[9]将最大后验概率估计(Maximum A Posteriori,MAP)译码算法网格图中增加相位变量θ,通过将相位等分,将相位估计和译码迭代联合完成。另一种无需修改译码器,利用译码器输出的软信息计算同步参数估计值,如图4所示。前者对于不同参数,需进行有针对性修改译码模块,通用性较差,实现复杂。后者无需对译码器进行修改,实现相对简单,主要有两种方式,一种是以最大似然估计准则为基础,N.Noels给出的基于EM算法的码辅助定时算法,二是利用译码后似然信息构造函数,通过搜索最大值来获得最优估计值。其中,基于EM算法的码辅助定时算法估计范围窄,适用性小,而构造似然函数法(以下简称M值法)可以获得全局最优值,估计范围宽,但需研究低复杂度的算法便于工程实现。因此,现有文献主要在该算法基础上进行改进。
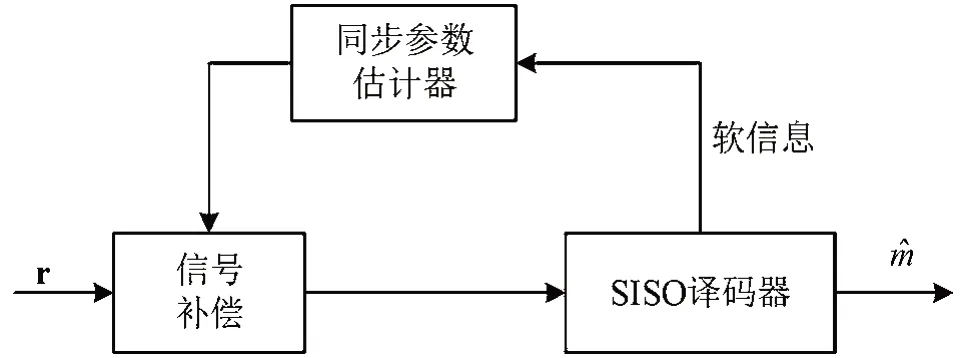
图4 基于软信息辅助的同步参数估计
2.2 基于M值函数的码辅助同步算法
基于M值函数的码辅助算法基本思想为,根据译码器输出信息的特性,按照一定规则设定同步参数量,构造代价函数,代价函数的最大值与同步参数量相关,当搜索得到函数最大值,则参数值相应估计出。
当同步参数存在偏差时,采用Gardner定时恢复算法的信号有效信噪比相应降低。以定时偏差为例,当定时偏差为τ时,接收信号rk可以展开为同向正交分量:

由式(1)知,由于定时偏差存在,送入译码器的信号不仅功率损失cos()φ,还产生一个干扰分量,可认为是噪声。因此,等效为有效信噪比降低。
LDPC译码器采用MAP译码算法,所得的符号概率对数似然比(Log-likehoodRatio,LLR)表达式为:
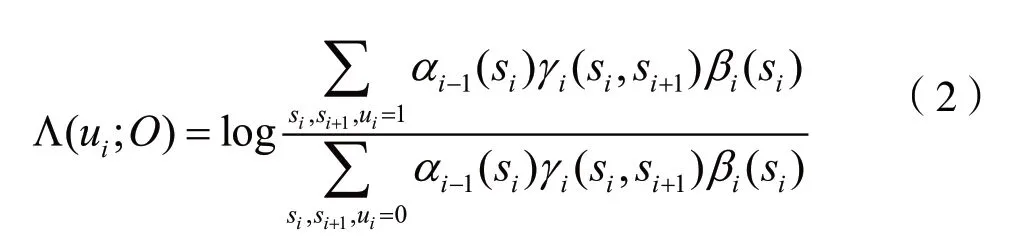
其中,γi(si,si+1)表示转移概率,αi-1(si)表示前向递推量,βi(si)表示后向递推量。由于存在定时偏差,有用信号幅度降低,进而使转移概率γi(si,si+1)降低。由于转移概率降低,对应的前向递推量αi-1(si)、后向递推量βi(si)也相应降低。
对于第k个比特,假设传输为1时(dk=1),从式(2)知,由于定时偏差的存在,LLR分子的值减少,而分母的值增加,则LLR的绝对值逼近0,反之对应于传输比特为0时(dk=0),LLR的绝对值也逼近0。对于不同位置的传输比特,对定时偏差的敏感程度不一。因此,从统计角度分析,当处于理想同步条件下,即估计出的定时偏差越准确时,绝对值均值可达全局最大。因此,绝对值和可作为定时偏差敏感度的统计量,可通过搜索代价函数极值可获得最优估计值。
下面以相位偏差为例,以绝对值平方和构造M值函数(式(3)),并用Matlab仿真验证结果。

图5给出了MSSO(τ^)与不同定时偏差τ^之间的关系曲线,仿真条件为LDPC编码方式、二进制相移键控(Binary Phase Shift Keying,BPSK)调制方式。可以看到,同理论分析一致,M值函数在定时偏差取值区间内只有一个最优值,即全局最优。且最优值为理想同步条件下(τ=0)。随着信噪比的提高,峰值越尖锐,即抵抗噪声能力越强,估计精度越高。
因此,我们通过搜索M值峰值位置来确定定时偏差。算法迭代步骤归纳如下:
(1)定义Δτ为搜索步长,按照式(4)生成一组定时偏差搜索值{τn}
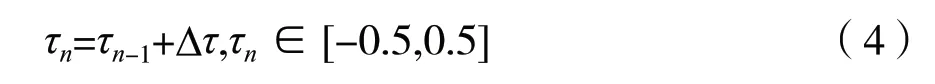
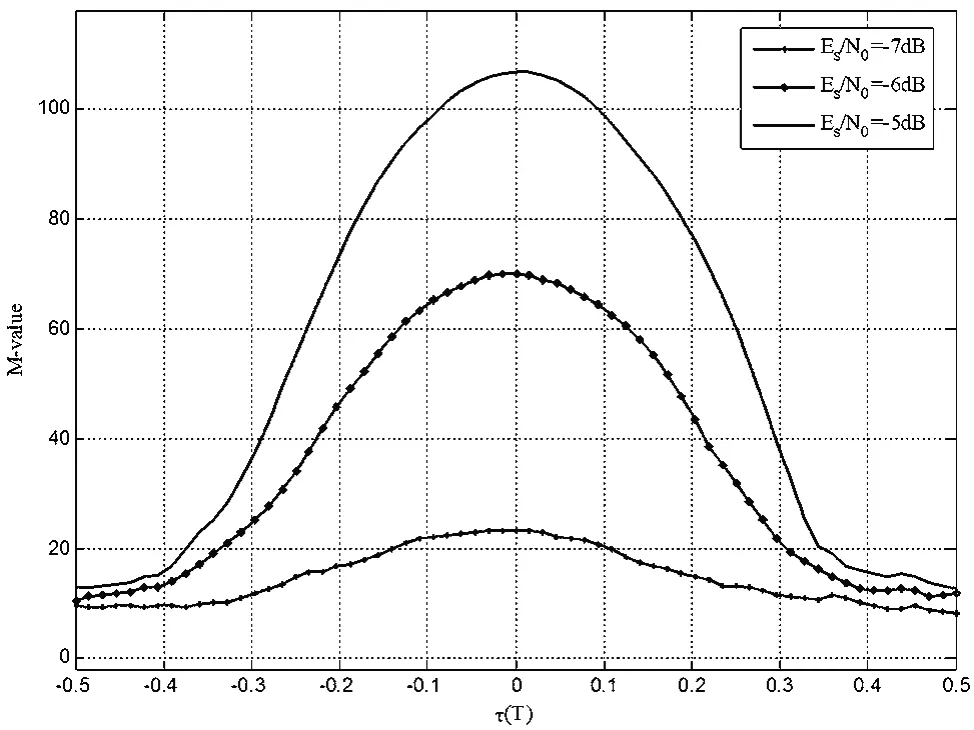
图5 M值函数与定时偏差及信噪比关系(p=2)
(2)对数据y(mTs)进行偏差为τn的定时校正,得到数据y(τn),送入译码器后得到M(τn);
(3)n=n+1,转向步骤1;
(4)通过比较,选择{M(τn)}最大值对应的τ^作为最终的估计值,即并获得最佳采样点数据y(τ^);
(5)将最佳采样点数据y(τ^)送入LDPC译码器译码,完成解调。
从上述算法实现知,M值搜索算法,复杂度主要取决于译码迭代次数,其迭代次数又由搜索步长Δτ决定。步长Δτ越小,估计精度越高,所需迭代次数越多,复杂度越高,反之,相反。以仿真中设置参数为例,搜索完成需要进行50次迭代,且完成搜索后,译码过程所需迭代需要在最优估计修正采样点之后进行。所需的复杂度很高,工程实际不易实现。
2.3 改进的基于三角插值码辅助定时算法
为解决直接搜索算法复杂度高的问题,文献[10]采取多级搜索方式,通过逐级压缩搜索范围来减小迭代量,但复杂度降低有限。文献[11]采用M值搜索压缩大定时偏差,再用EM算法迭代求解出最优值,有效减少了迭代次数,算法实现复杂度依然较高。本节针对M值函数曲线特性,提出一种基于三角插值的M值码辅助同步算法,将其应用于DVBS2X定时同步跟踪模块中,则可以较低的复杂度情况下,获得更好的定时估计性能。
由图5曲线可以看出,随着信噪比的变化,曲线始终呈类抛物线型,借助于插值理论,我们可以考虑利用已知N个点的采样值插值出最优值及最优值所在位置。文献[12]给出了一种新的内插滤波器—三角多项式插值滤波器插值,插值精度优于多项式插值。某处函数值可由其附近N个点(N为偶数)的采样值经插值得到,具体描述如下:
已 有N个 样 值y(n)(n=-N/2+1,…N/2),则 在μ(0≤μ≤1)处的内插值为:

对于实信号,由于ck与c-k共轭,因而有:
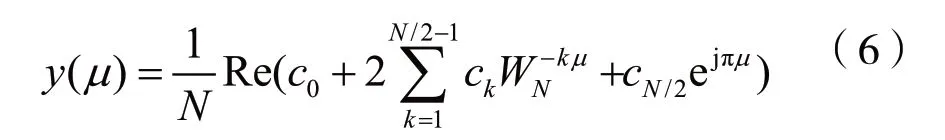
则对于N=4时,插值系数为:

根据y(t)对称的性质,式(6)中高次谐波项很小,对运算结构无显著影响,可将其忽略,因此,式(6)可简化为:
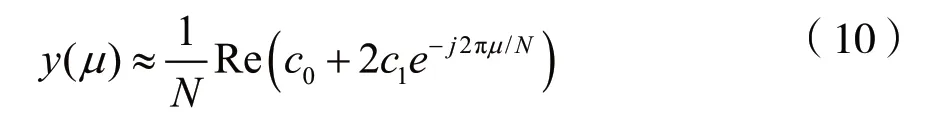
则求取上式最大值可得

则应用到本节给出的场景,我们对匹配滤波器后信号4倍等间隔采样,并将4组数据送到译码器,可获得4个M值,即N=4,分别记为Γ(-T/4),Γ(0),Γ(T/4),Γ(T/2)。由式(11)可得定时估计值为:
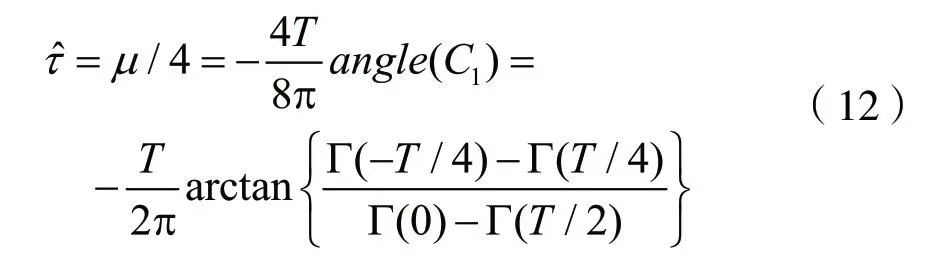
其中,式(12)除以4,原因为式(11)的参考基准为1,而实际采样间隔为0.25。需要注意的是,由于使用式(5)要求0≤μ≤1,则使用三角插值前提条件为定时偏差τ满足τ∈[0,0.25]。为满足整个区间估计需要,需要设定参考基准点。
基准点获取及算法具体实现步骤归纳如下:
(1)对经过匹配滤波后的信号进行4倍速率采样。
(2)以现有采样基准为参考,分别偏移-3T/4, -T/2,-T/4,0,T/4,T/2,3T/4,获得7组数据,将 7组数据分别送入译码器后得到相应的M值 Γ(-3T/4),Γ(-T/2),Γ(0),Γ(-T/4),Γ(T/4),Γ(T/2),Γ(3T/4)。
(3)比较7组数据M值大小,由图4可知,距真实值越近,M值越大,则可确定相应真实值所在区间,进而确定参考基准点。假设定时偏差τ=-0.35,则可确定基准点为Γ(-T/2),则以此基准点为参考可获得调整后采样4组数据,即 Γ´(-T/4)=Γ(-3T/4),Γ´(0)=Γ(-T/2),Γ´(T/4)=Γ(0),Γ´(T/2)=Γ(T/4)。
(5)滤波器获得一组最佳估计采样点为y(τ^),送入译码器并完成译码。
3 改进算法性能及复杂度分析
3.1 性能分析
下面以LDPC码,BPSK传输系统,采取三角插值编码辅助算法,按照如上实施步骤,并同M值搜索算法性能进行比较。M值算法仿真参数为搜索步长Δτ=0.02。
图6出了在信噪比Eb/N0变化的情况下均方根差(Root Mean Squared Error,RMSE)性能曲线。
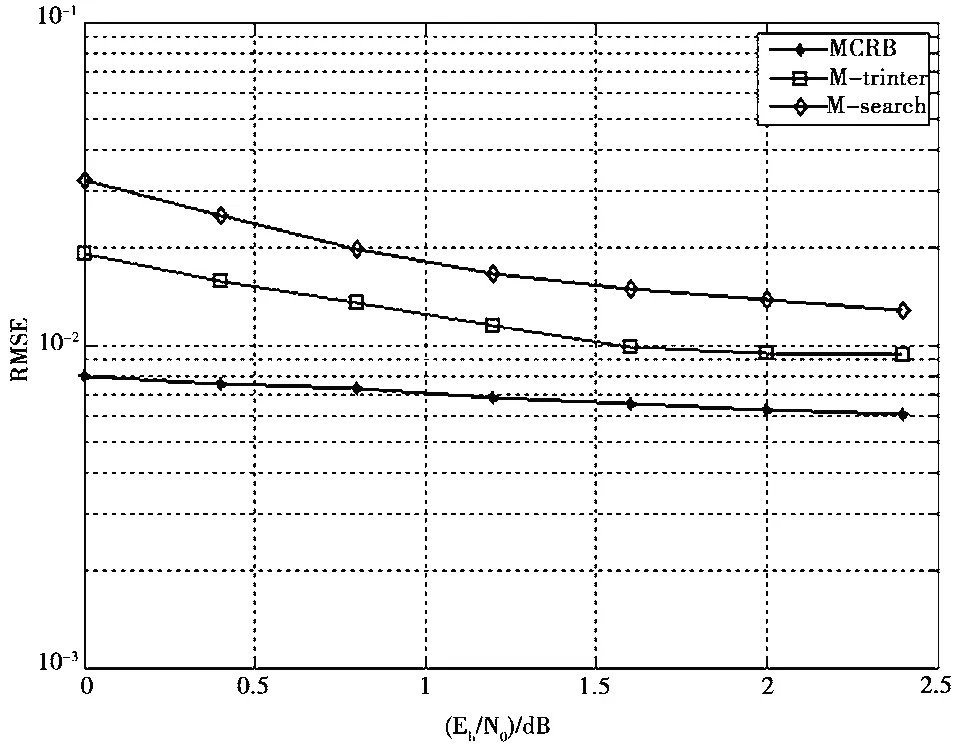
图6 进码辅助算法RMSE性能
如图7所示,信噪比Eb/N0=1.5 dB条件下,两种算法平均估计值(MEV)的性能曲线。图8给出了两种算法RMSE性能随定时偏差变化的情况。
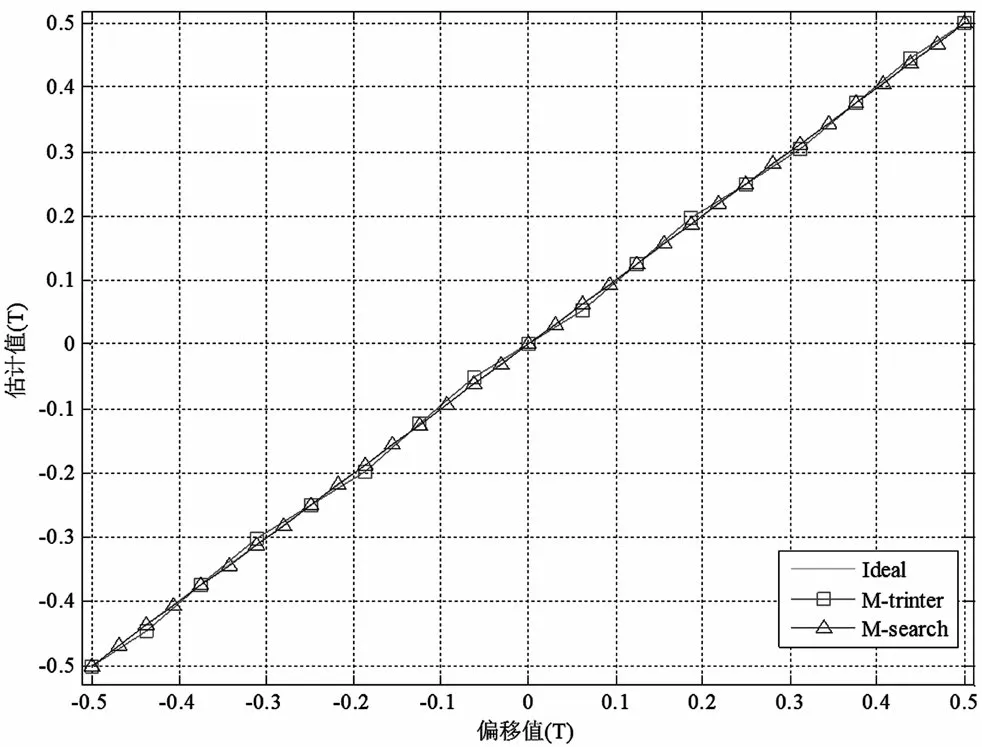
图7 码辅助算法MEV性能(Eb/N0=1.5 dB)
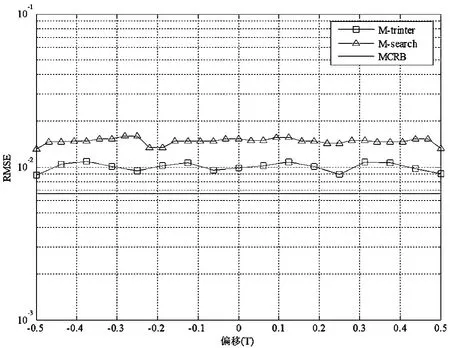
图8 码辅助算法RMSE性能与定时偏移关系(Eb/N0=1.5 dB)
由图6可知,对比于M值搜索算法,三角插值算法估计性能更优,这是因为理论上,直接搜索算法可以获得全局最优值,精度应最高,但直接搜索法由于搜索步长设置为固定值,精度往往偏离理论最优,导致搜索算法性能劣于三角插值算法,进一步表明本文提出的改进算法同等条件下抗噪声性能更好。如图7、图8所示,两种算法在整个定时变化区间内均为无偏估计,表明算法可以适应于大抖动,实用性强。
3.2 复杂度分析
由算法实现知,算法复杂度主要从迭代次数和插值次数分析。为获得最优估计值,M值搜索算法获得最有估计值需要50次,且每次都需要通过内插滤波器获得修正值;基于三角插值码辅助算法仅需迭代7次,而三角插值码辅助算法只需要通过调整采样时间,可以获得修正值,如对于数据组y(3T/4),为获得数据组y(T/4)只需向左多存储一个采样点即可,无需额外的插值运算。表1从迭代次数和插值次数两方面给出了两种算法计算复杂度比较,参数设置同上。

表1 算法计算复杂度比较
综上,可以看到,改进的插值算法既有M值搜索算法全局最优特性,也通过插值减少了搜索运算量,在精度和复杂度方面均获得优化,易于工程实现。
进一步,为解决Gardner算法在低信噪比环境下估计性能差的问题,我们将优化的编码辅助算法应用于DVB-S2X的定时跟踪模块,修改后的定时跟踪模块框图如图9所示。通过利用LDPC编码后码字间相关特性,在定时同步基本建立的情况下,进一步提升定时同步性能。
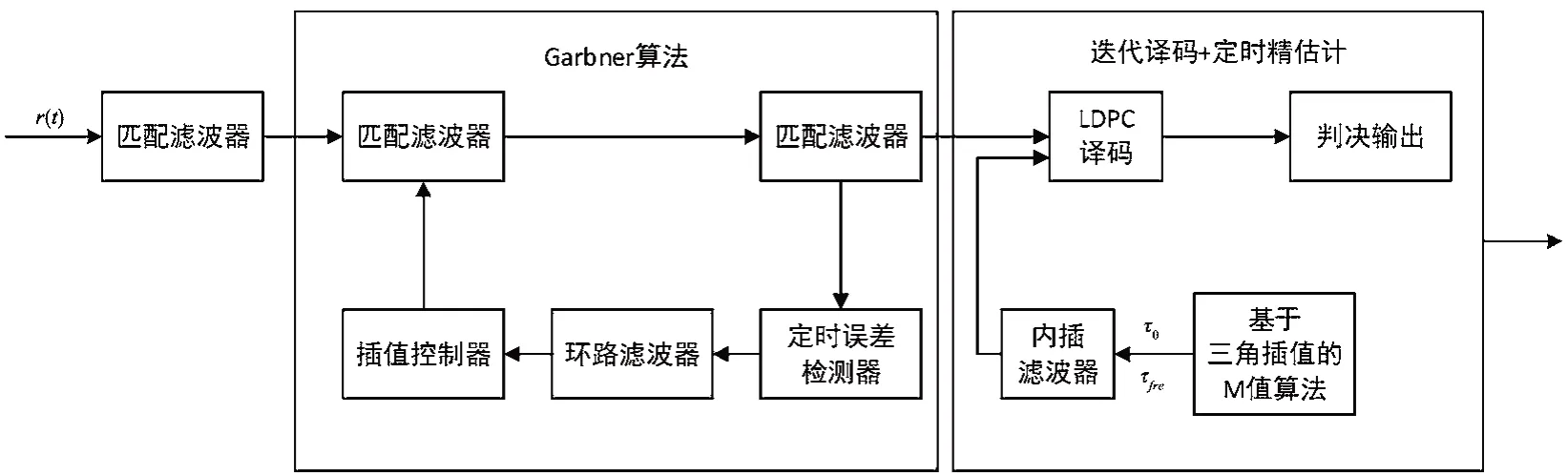
图9 改进的DVB-S2X定时同步算法框图
图10给出了引入编码辅助算法和未引入编码辅助算法下,定时同步偏差的估计性能对比情况,可以看到,引入本文提出的DVB-S2改进算法后,算法的性能得到较大提升,并能够有效抗线路衰落情况。
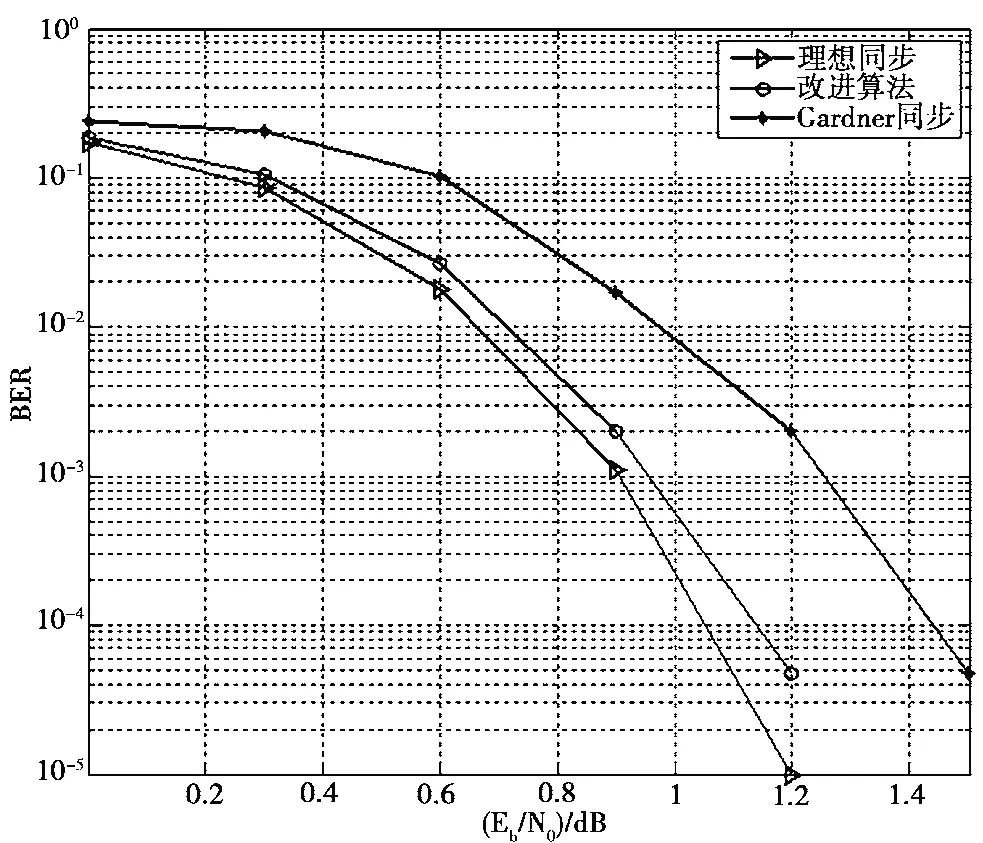
图10 引入编码辅助算法和未引入编码辅助算法下,定时同步偏差的估计性能对比情况
4 结 语
本文针对DVB-S2X接收系统中的定时同步展开研究,首先对定时同步模型入手,进而对现有DVB-S2X的Gardner定时同步算法进行简单的性能分析,并指出了不足。接着,利用LDPC编码的内联特性,引入了编码辅助定时同步算法,在此基础上,提出了一种改进的基于三角插值的码辅助算法,在保证估计性能和估计范围基础上,复杂度得到优化,并将其引入到DVB-S2X结构,构建跟踪模块。仿真表明,该算法有效解决极低信噪比场景下定时同步的抖动,进一步提高了系统同步性能,为新一代数字卫星广播标准下的接收系统终端小型化提供技术支持。
