基于数字信道化方法的跳频信号接收研究*
2019-06-10吴明钦
吴明钦
(中国西南电子技术研究所,四川 成都 610036)
0 引 言
跳频通信是靠载频的随机跳变来躲避干扰,将干扰排斥在接收信道以外来达到抗干扰的目的,避免敌方电台的测向和干扰。跳频通信技术在抗干扰通信方面的突出优势,使其在通信装备中得以广泛应用。跳频频率数越多,跳频速率越高,其抗干扰性能越好[1]。
信道化接收机瞬时频带宽,能实现宽带侦察。早期的信道化接收机采用模拟电路实现,即用模拟滤波器组把接收频带分割为许多邻接信道。当瞬时频带很宽时,需要非常多的滤波器,增加了电路的设计调试难度。而在软件无线电数字信道化接收机中,信道化由数字化方法实现,能有效地简化 接收设备[2]。
1 数字信道化的多相DFT结构
本节在分析低通滤波器组结构的基础上,给出多相DFT结构的一般推导形式。信道化首先由滤波器组完成信道的分离,即将0~fs或0~2π带宽的信号划分为多个子信道,用滤波器取出子信道中的信号。均匀信道是最常用的划分方式。例如将0~2π均匀划分为K个子信道,考虑到实际滤波器存在过渡带及降低原型低通滤波器的阶数,将整个接收机输入带宽覆盖,消除接收频带盲区,则将原型低通滤波器的通带频率设定在ωp=π/K,阻带频率设定在ωs=2π/K。这样的划分方法将会使相邻信道的响应存在重叠区域[3]。如图1所示。
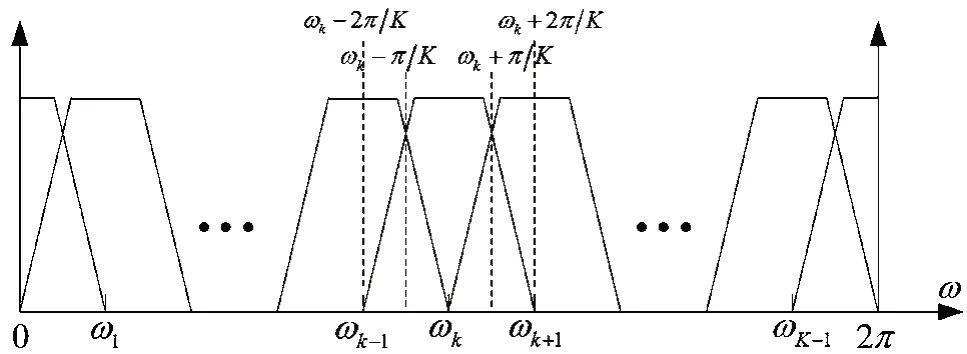
图1 信道划分示意图
低通滤波器组的信道化结构,如图2所示。滤波器组的每一支路就是DDC的复数形式。设信道数为K,抽取因子D,两者满足K=FD(F是正整数)的关系。ωk,k=0,1,…,K-1,是各信道的中心频率,若F=1,则子信道输出数据率与信道带宽相等,即临界抽样。

图2 低通滤波器组信道化结构
设图2中的h(n)为N阶低通FIR滤波器,可以得到第k个信道的输出为:
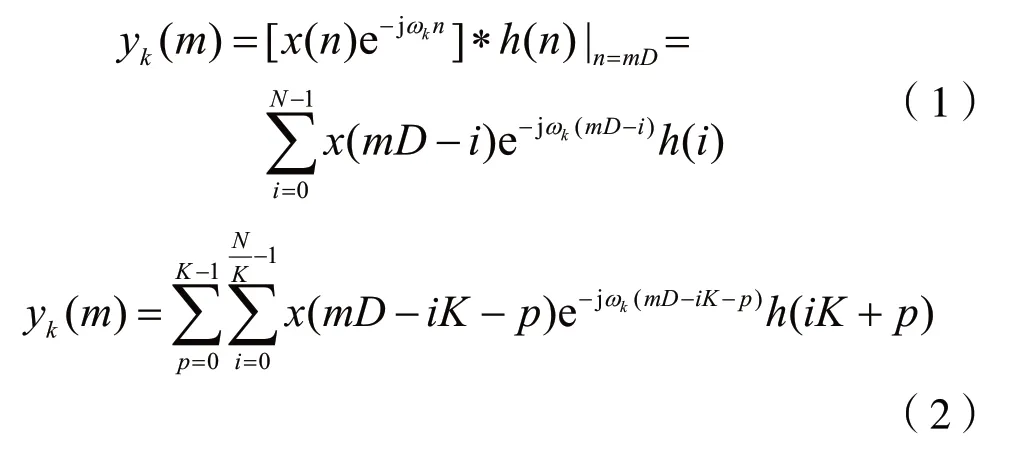

按图1的信道划分方法,此时ωk=2πk/K。代入式(5)有:

根据式(6)和式(7)可得到按图1信道划分的数字信道化的多相DFT结构,如图3所示。

图3 多相DFT信道化结构
由图3可见,此时不仅D倍抽取器已经位于滤波器之前,而且现在每个信道的抽取滤波器不是原型低通滤波器h(n),而是该原型低通滤波器的多相分量,其运算量降至原来的1/D,极大的提高了这种信道化接收机的实时处理能力。另外,图中的IDFT可以采用其高效算法FFT来实现,也保证了高速的运算速度。同时,图3为硬件实现该算法提供了直接的高效运算结构。
2 信道判决
首先讨论信道输出存在的问题。由于实际滤波器响应存在过渡带,为了覆盖整个接收机接收带宽,按图1进行信道划分,相邻信道的滤波器响应存在重叠区域,则在相邻信道之间存在相互干扰。最坏的情况是,当接收到一个脉冲信号,由于脉冲信号的上升沿和下降沿包含大量的宽带能量,这些能量会进入相邻信道和非相邻信道。这种现象被称之为“兔耳效应”[4]。由于滤波器的脉冲响应特性导致信道滤波器对于输入脉冲信号的时域输出响应出现一个峰值分别对应脉冲信号的上升沿和下降沿的位置。
如果信号落到信道交叠区,则两个信道的输出都会出现信号,那么应该对哪个信道的输出作信号处理呢?仅仅提高滤波器的频响特性不能解决这一问题。滤波器过渡带和信号属性导致一个输入信号在多个信道中出现的情况称为信道模糊[5]。
下面讨论信道的判决方法。为了降低“兔耳效应”对信道输出判决的影响,需要对每个信道输出设置一个最小脉冲幅度门限和一个最小脉冲宽度门限。当信道输出幅度超过最小脉冲幅度门限,则开始脉冲宽度计数器计数;当信道输出幅度低于最小脉冲幅度门限,则停止脉冲宽度计数器计数,接着将该计数值与最小脉冲宽度门限比较。如果超过最小脉冲宽度门限,则判定为接收到一个有效脉 冲信号。
对于信道模糊的问题,可借助瞬时幅度。当某信道中有稳定信号时,观察相邻的两个信道是否有信号出现,若有则比较两信道的幅度值,将信号判定到幅度较大的信道。还可以借助瞬时频率信息做判决。根据图1的信道划分,要将一个信号判定到信道k,则有:

满足上述假定的频率应该在(ωk-2π/K,ωk+ 2π/K)范围内,经抽取混频后,则有:

为了保证抽取后信道输出信号不发生混叠,信道数目和抽取倍数应满足K/D≥2,这就是瞬时频率测量对信道带宽和抽取倍数的约束。为了获得最大抽取率,此时有K=2D,代入式(9)有:

为判定信号在第k个信道的条件。
对于跳频信号来说,其载频是在随机的跳变,这样跳频信号对于信道化接收机的每个子信道来说都是载频在变的短时脉冲信号,子信道输出将会出现“兔耳效应”现象。并且跳频信号载频的随机跳变也会出现在某个时刻,频率落在两个相邻子信道的重叠区域,这样子信道输出存在信道模糊的问题[6]。
综合上述的讨论,可得到如下的信道判决方案,如图4所示。

图4 信道判决框图
3 仿真结果
设信道按图1划分,信道数目K=16,抽取率D=8,采样率为16 MHz。输入信号为跳频基带信号,跳频信号的参数是跳频速率10 000 H/s,跳频频率集为8。只发送8个跳频码,跳频编码选0~7的递增序列,则样本点数取128 00。输入信号信噪比为10 dB。跳频编码与频率值的对应关系如表1所示。仿真图如图5所示。
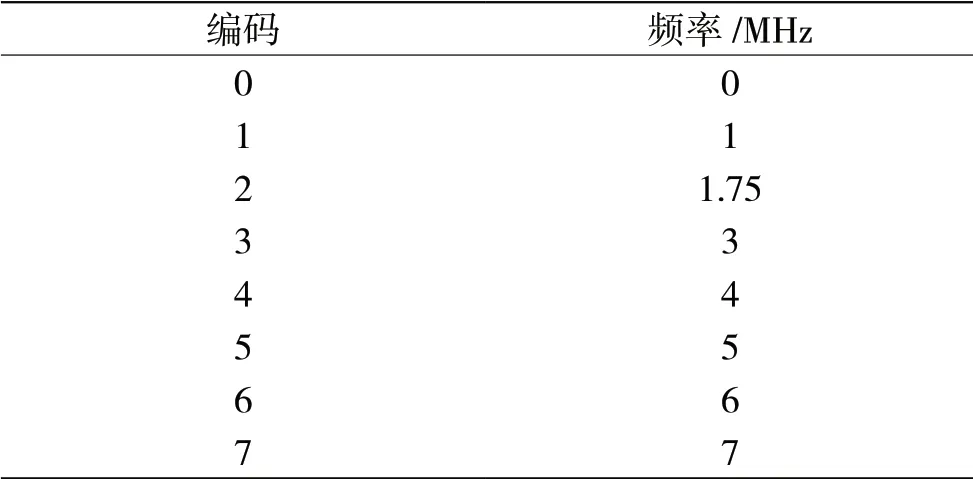
表1 调频编码与频率值对应关系

图5 仿真信道输出幅度
从图5中可看到,在0.4~0.6 ms之间,接收到编码2,对应的跳频载频1.75 MHz正好落在信 道1和信道2的重叠区域,此时两个信道同时有信号输出,但信道1输出的瞬时幅度低于信道2输出的瞬时幅度。可以采用比较相邻信道输出瞬时幅度值的方法判定当前信号落在信道2中。同时也可以根据信道输出的测频结果判定,此时信道1输出计算角频率值为而信道2输出计算角频率值为则可以判定当前信号落在信道2中。
4 结 语
本文讨论了一种便于硬件高效实现的数字信道化方法,联合使用信道输出的瞬时幅度和瞬时频率信息做出信道判决,用于跳频信号的接收。文中给出了数字信道化多相DFT结构的一般推导形式。通过优化选取关系式K=FD中系数F,给出了简单并且可靠的信道判决方案,降低了对相邻信道重叠区域信号误判的可能性。
