基于SURF算法的双目视觉特征点定位研究

王永锋 石超 徐子锋 陈龙

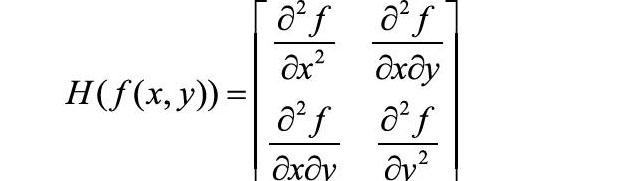
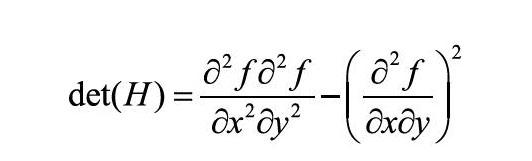
摘  要：针对双目视觉立体图像特征点匹配质量不好导致定位精度低的问题，本文提出改进SURF匹配的特征点定位方法。在改进的SURF匹配算法中，采用双向匹配、NNDR约束、对称性约束、极线约束和交叉匹配约束的方法，提高了图像特征点匹配的质量。在双目视觉特征点定位中，采用公垂线段中点法具有更高的特征点定位精度。实验证明，该算法的特征点定位精度更高，同时可以达到实时三维重建效率。

关键词：特征点重建;SURF算法;双目视觉;最小二乘法;公垂线段中点法

中图分类号：TP391     文献标识码：A

Abstract：Aiming at the problem of low positioning accuracy caused by poor matching quality of binocular stereo image feature points，this paper proposes a feature point 3D reconstruction method based on improved SURF matching algorithm.In the improved SURF matching algorithm，two-way matching，NNDR constraint，symmetry constraint，polar line constraint and cross matching constraint are used to improve the quality of image feature point matching.In binocular vision feature point positioning，the common vertical midpoint method has higher feature point positioning accuracy.Experimental results show that the proposed algorithm has higher accuracy of feature point positioning and can achieve real-time 3D reconstruction efficiency.

Keywords：reconstruction of feature points;SURF algorithm;binocular vision;least square method;midpoint method of

common vertical segment

1   引言（Introduction）

隨着工业4.0时代来临，工业机器人智能化应用空前广泛，机器视觉定位作为机器人技术智能化发展的重要分支之一，其准确度的提高成为人们研究的热点[1]。在机器视觉定位中，双目视觉具有测量范围广和定位精度高的特点，越来越多地出现在工业领域中[2]。

在双目视觉系统中，目标物体特征点的匹配精度和重建精度是影响双目视觉系统定位准确性的主要因素，因此在这两方面的研究受到广泛的关注。在立体图像特征点匹配中，SURF算法的匹配效果比较稳定，但同时存在错误匹配现象。在物体特征点重建中定位精度要求高的场合，最小二乘法的定位精度不能满足需求。

为此，本文提出改进SURF匹配的特征点重建方法，通过实验对比其匹配效果和重建精度。

2   SURF算法和双目立体视觉（SURF algorithm andbinocular stereo vision）

2.1   SURF匹配算法原理

SURF算法主要由特征点检测、主方向的确定、特征描述的构建及特征点匹配等四部分构成。

SURF算法采用Hessian矩阵行列式近似值图像[3]。式（1）为任意像素点的Hessian矩阵计算公式：

矩阵判别式如式（2）所示，根据其计算结果正负来定位图像特征点。

在SURF算法中，以特征点为圆心，一定大小尺度为半径的圆形领域内，将60°扇形区域作为扫描单位，首先统计该区域中水平方向的haar小波计算值，然后再统计此区域垂直方向haar小波计算值，最后将两者的统计结果值相加，重复扫描统计，其结果值最大的方向为特征点的主方向。

SURF算法构建特征描述的基本流程是，首先以选定特征点为中心，建立一个边长为一定尺度大小的正方形包围框，该框方向为检测出特征点的主方向。然后将正方形包围区域等分为16个小正方形区域，在划分的小正方形区域中先统计水平方向的haar小波计算值和其绝对值，再统计垂直方向的haar小波计算值和其绝对值，这样每一个小正方形区域都可以用一个四维向量来表示：

重复统计计算每一个形区域，统计完毕后，每个特征点可以用一个64维的向量来描述。

在图像匹配中，求得两张图像各特征描述向量后，根据第一张图像某特征点的描述向量，统计第二张图像各特征描述向量与该特征描述向量的得分值，在特征点匹配中，得分值的好坏是用欧氏距离的大小来衡量的，距离越小，得分值越大，匹配效果越好。

2.2   双目视觉特征点定位原理

（1）特征点三维重建工作流程

特征点三维重建工作流程如图1所示。

（2）特征点三维重建模型

空间特征点三维重建的基本模型如图2所示，对于空间特征点任意一点，像素点和分别为空间点在左右相机像平面的投影点，但是仅仅通过单一像素点或无法获取到特征点三维坐标，由于在直线或上的任意点，在像素平面上的投影点都为点或。所以，利用两个相机拍摄图片，这样直线和可以唯一确定点的位置，实现特征点的三维重建。

3   改进的SURF匹配算法（Improved SURF matchingalgorithm）

本文采用经典SURF算法检测到左右图片特征点后，采用汉明距离完成初步匹配，但是由于存在许多错误特征点对，因此需对SURF匹配算法进行改进，设计流程图如图3所示。

实现的具体步骤如下：

（1）读取左右相机图片，SURF特征点检测和特征描述。

（2）分别计算左图到右图的匹配集，右图到左图的匹配集。

（3）NNDR约束[4]（最近邻比例策略），分别对、集合中的匹配点做NNDR约束处理。

（4）对称性测试[5]，例如在集合中特征点a对应特征点b，则判断集合中特征点a是否对应特征点b，若完全对应相同，则保留该特征点匹配对;否则，筛选掉该特征点匹配对。

（5）采用PROSAC算法[6]计算基础矩阵F，筛选掉不能通过极线约束[7]测试的特征点匹配对。

（6）交叉匹配約束[5]，经过步骤（5）处理后，得到的特征点匹配对理论上不会出现交叉现象，反之筛选掉交叉现象的匹配点对。

3.1   最近邻约束和对称性检测

经典SURF匹配算法自身存在错误匹配现象，为了有效提高特征点匹配准确率，本文考虑加入最近邻约束和对称性检测。

（1）选取左图片中的特征点，在右图片中找到最优质的匹配点，直至左图片特征点全部匹配完成，得到匹配集合;同理，对右图片执行相同的操作，得到集合。

（2）在匹配集合中，计算某一特征点匹配的最短距离与次短距离的比值，通过设置阈值来筛选特征点匹配对。如果，则将匹配结果存入点集;对于匹配集合，同理，得到点集。

（3）将两个点集、执行求交操作，得到经过最近邻约束和对称性检测的匹配集合，即。

3.2   利用PROSAC算法剔除误匹配

PROSAC算法是在RANSAC算法[8]的基础上改进而来的，RANSAC算法是通过随机抽取样本估计参数模型，而PROSAC算法是将样本数据排列，选取匹配质量好的数据进行匹配来估计参数模型，加快特征点匹配的速度。

具体步骤如下：

（1）将集合C按照汉明距离由小到大排序，选取集合C中前m个特征点对。

（2）从m个特征点对中随机抽样选取四个，计算对应图像的基础矩阵H。

（3）根据步骤（2）求出的变换矩阵计算其他特征点对的误差，确定该匹配点对是否为内点，并且统计内点个数。

（4）判断内点个数是否超过给定阈值，若超过给定阈值，则当前计算的基础矩阵为最优矩阵，否则，再从m个特征点对中随机抽样选取四对，进行下一次迭代。

（5）如果当前迭代次数达到最大迭代次数，则返回内点数目最多的一组参数模型，得到最优质的基础矩阵H。

3.3   交叉匹配约束

对于通过极线约束测试的匹配集合，还可能会出现交叉匹配的错误匹配现象，如图4所示，直线和分别是左右图像上两条对极线，通过极线约束测试两组匹配点对和，理论上，例如在第一张图片的极线上，点位于之上，那么在第二张图像对应极线上，点也应该位于之上。所以添加交叉匹配约束步骤处理，可以得到更优质的匹配集合。

4   空间特征点定位（Spatial feature point positioning）

如图2所示为理想情况下的双目视觉特征点三维重建模型，由于存在相机标定和像素特征点匹配误差，导致左右相机确定的两条直线或可能不会相交于点P，所以需要建立近似模型估计点P的三维空间坐标。

特征点三维重建的传统做法是采用最小二乘法[9]，但是它在求解过程中没有将成像模型的几何意义考虑在内，重建精度有待提高，所以本文采用公垂线段中点法[9]来提高特征点的三维重建精度。

如图5所示为公垂线段中点法示意图，理论上空间点P为两条反射线、的交点，但在实际计算过程中，由于计算误差的存在，两条直线、很可能是两条空间异面直线。

公垂线中点法的步骤是：首先求解两条异面直线的公垂线，然后求解公垂线与两条直线的交点坐标，最后取两个交点的中点坐标作为特征点三维重建坐标。在求解过程中，需要考虑以下两点：

（a）如果两条异面直线的公垂线段大于设定阈值，则判定该匹配点对为错误匹配。

（b）如果公垂线段的长度为0，则认为两条直线不是异面直线，特征点三维重建转化为两条空间直线求交点的问题。

具体公式推导如下所示：

文献[9]说明，经过化简，每条异面直线或都可以列出两个等式，因为点A、B分别在异面直线、上，有四个方程，联合上式，得到关于六个未知数的六个线性方程，可解得，则重建空间点坐标为。

5   实验结果与分析（Experimental results and analysis）

5.1   特征点匹配结果与分析

为了验证本文算法的精确性和实时性，将SURF算法、SURF+NNDR算法、SURF+RANRAC算法和本文算法进行验证和比较，其匹配结果如图6所示。

表1为四种算法的匹配结果对比。

精确性上来说，SURF算法出现明显的错误匹配现象;SURF+NNDR算法是在SURF匹配的基础上，加入NNDR约束，在一定程度上可以剔除大部分错误匹配点; SURF+RANRAC算法是在SURF匹配的基础上，采用RANRAC进行进一步剔除质量不好的匹配点对，提高了匹配的精确性;本文设计的算法在SURF算法匹配的基础上，采用对称性约束、PROSAC算法及交叉匹配约束算法，获取到更优质的匹配点对。

匹配速率上，由于SURF+NNDR约束算法、SURF+RANRAC算法和本文算法都是在SURF算法的基础上改进而来的，消耗的时间比经典SURF算法多。其中SURF+RANRAC算法和本文算法的立体匹配效果最好，与SURF+RANRAC算法相比，本文算法的运行速率更快，满足实时性需求。

5.2   特征点三维重建结果分析

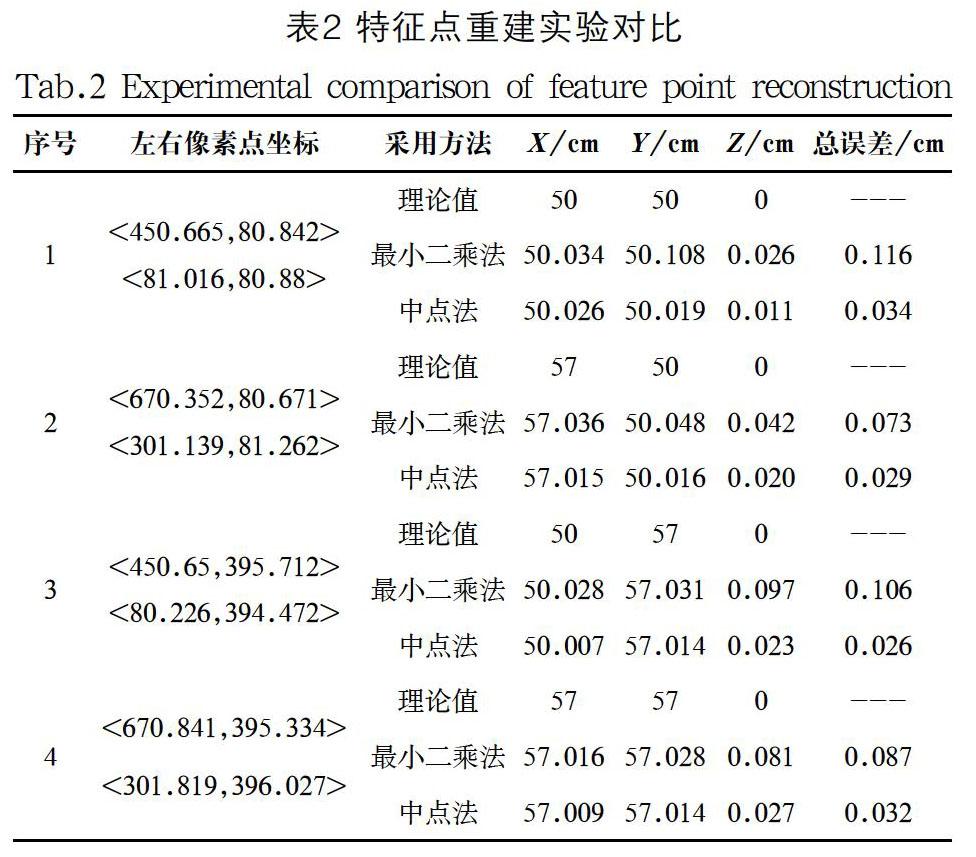
实验采用两个大恒MER-500-14GM工业相机，两个相机镜头的基线距为200mm，以标记图案的左上角点为坐标原点，建立世界坐标系。对标记图案中的四个标记点进行三维定位，将理论值与两种方法求取值相比较，对比结果如表2所示。实验表明，与最小二乘法相比，公垂线段中点法有更高的定位精度。

6   结论（Conclusion）

本文提出改进SURF匹配的特征点定位方法，在图像匹配算法方面，实验结果证明，该算法匹配效果很好，解决了匹配质量不高的问题;在双目视觉特征点定位方面，实验结果证明，该算法有更高的定位精度。同时本文设计的方法具有很快的运行速度，重建效率高。

参考文献（References）

[1] 汤勃，孔建益，伍世虔.机器视觉表面缺陷检测综述[J].中国图象图形学报，2017，22（12）：1640-1663.

[2] 黄鹏程，江剑宇，杨波.双目立体视觉的研究现状及进展[J].光学仪器，2018，40（04）：81-86.

[3] Bay H，Ess A，Tuytelaars T，et al.Speeded-Up Robust Features （SURF）[J].Computer Vision & Image Understanding，2008，110（3）：346-359.

[4] Park H，Mitsumine H，Fujii M.Automatic Adjustment of the Distance Ratio Threshold in Nearest Neighbor Distance Ratio Matching for Robust Camera Tracking[J].IEICE Trans on Information and Systems，2011，E94-D（4）：938-940.

[5] 陳洁，高志强，密保秀，等.引入极线约束的SURF特征匹配算法[J].中国图象图形学报，2016，21（08）：1048-1056.

[6] Chum O.Matching with PROSAC-progressive sample consensus[J].Proc.conf.on Cvpr，2005，1（2）：220-226.

[7] Sui L，Zhang J，Cui D.Image Rectification Using Affine Epipolar Geometric Constraint[C].International Symposium on Computer Science & Computational Technology，2008，4（1）：26-33.

[8] 秦晓飞，皮军强，李峰.基于极线约束的ORB特征匹配算法[J].计算机应用研究，2018，35（09）：2865-2868.

[9] 罗世民，李茂西.双目视觉测量中三维坐标的求取方法研究[J].计算机工程与设计，2006（19）：3622-3624.

作者简介：

王永锋（1992-），男，硕士生.研究领域：图像处理，机器视觉.

石   超（1993-），男，硕士生.研究领域：数字图像处理.

徐子锋（1993-），男，硕士生.研究领域：智能制造.

陈  龙（1978-），男，博士，副教授.研究领域：产品计算设计，机器视觉与机器人.