对2018年全国卷Ⅲ理科21题（Ⅱ）的质疑*

☉四川内江师范学院数学与信息科学学院 刘成龙

☉四川省泸州市泸州高级中学 吕荣春

百度百科对质疑的解释是提出疑问.提出疑问是创新的重要表现，敢于质疑是科学研究的良好品格.有质疑、有争鸣才能唤醒固化的思维，才能在碰撞中闪现智慧的火花.2018年全国卷Ⅲ理科第21题（下文简称21题）无论是参考答案，还是试题命题上都存在值得质疑的地方，本文将从四个角度对21题提出质疑.

一、试题再现

已知函数f（x）=（2+x+ax2）ln（x+1）-2x.

（Ⅰ）若a=0，证明：当-1＜x＜0时，f（x）＜0；当x＞0时，f（x）＞0.

（Ⅱ）若x=0是f（x）的极大值点，求a.

二、四点质疑

质疑之一：证明过程严谨吗？

答案是试题的重要组成部分.考试中心提供的（Ⅱ）的参考答案（华西都市报刊登）有不妥之处，为了行文方便先摘录如下：

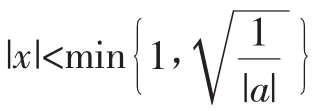
（Ⅱ）（ⅰ）由（Ⅰ）知，当x＞0时，f（x）＞（2+x）ln（1+x）-2x＞0=f（0），这与x=0是f（x）的极大值点矛盾.（ⅱ）若a＜0，设函数由于当时，2+x+ax2＞0，故h（x）与f（x）的符号相同.又h（0）=f（0）=0，故x=0是f（x）的极大值点当且仅当x=0是h（x）的极大值点.

如果6a+1＞0，则当，且时，h′（x）＞0，故x=0不是h（x）的极大值点.

如果6a+1＜0，则a2x2+4ax+6a+1=0存在根x1＜0，故当时，且时，h（′x）＜0，所以x=0不是h（x）的极大值点.

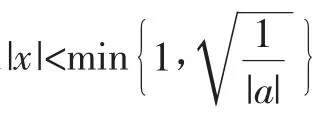
如果6a+1=0，则

当x∈（-1，0）时，h′（x）＞0；当x∈（0，1）时，h′（x）＜0.所以x=0是h（x）的极大值点.综上

疑问：上述证明中利用“2+x+ax2＞0，h（x）与f（x）具有相同的极大值点x=0.”的依据是什么呢？是显然的吗？我们认为这并不显然.事实上，若m为大于零的常数，则具有相同的极值点，这是显然的，但2+x+ax2为大于零的变量，此时h（x）与f（x）还具有相同的极值点吗？这需要证明，但参考答案并没有给出解释，且这个“结论”在中学教材上也找不到根据.解答上述“结论”需要借助以下引理：

已知函数f（x）满足f（0）=0，函数g（x）满足：存在δ＞0，使得对任意的x∈（0，δ），都有g（x）＞0恒成立，令h（x）=，则x=0是（fx）的极大值点的充要条件是x=0是h（x）的极大值点.

这个引理的证明，需要深刻理解邻域的概念及符号的表达，而高中生没有接触过邻域的概念，更谈不上运用符号语言进行证明，所以看似显然的结论其实并不显然.

因此，21题第（Ⅱ）问的参考答案不严谨.

质疑之二：试题背景公平吗？

试题背景指命题时选取素材中含有的知识、模型、问题、思想和方法，这些知识、问题、思想和方法称为数学背景.我们不禁要问该试题背景公平吗？

21题含有丰富的高等数学背景，借助高等数学工具能够快速解答，比如：借助极值点的第二充分条件，由f（3（）0）=0且f（4（）0）＜0可得又如，根据极大值点的定义：当x∈（0，δ）时，f′（x）＜0，因为δ可以无限趋近于0，可直接使用洛必达法则，得，同理可得进而得到；再如，由y=ln（x+1）在（1，2）阶的帕德逼近函数为，结合函数表达式可直接看出答案为很明显熟悉高等数学背景的同学解答本题几乎没有什么障碍，但因不熟悉高等数学背景而使用初等解法求解却难于上青天.

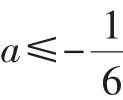
因此，21题第（Ⅱ）问背景明显不公平.

质疑之三：试题选拔功能真的好吗？

《普通高中数学课程标准（2017年版）》指出：“高考是我国最为重要的选拔性考试，数学高考命题应依据人才选拔的要求，发挥数学高考的选拔功能.”［1］我们不禁要问21题的选拔功能真的好吗？

从对考生的访谈来看，绝大部分考生认为试题太难，不知道怎么下手；从对教师的访谈来看，多数教师认为试题解答涉及精妙的构造，有浓浓的大学数学分析味道，以至于所给的参考答案很难看懂；从阅卷场反馈的信息来看，某省近30万理科考生近乎无人用初等解法做对，且用高等解法做对的不足30人，可见，用初等解法做对的比例几乎为零，用高等解法做对的比例也不足万分之一.不难看出，就算是运用高等解法解答正确的比例也远远低于“名校”的招录比例，甚至低于“一本”的招录比例，显然以此来选拔人才不具有科学性和合理性.同时，从试题命制层面上看，21题难度系数远低于0.2，按考试大纲规定难度在0.2以下的试题不宜出现在试卷中.

因此，21题第（Ⅱ）问不具备良好的选拔功能.

质疑之四：试题的导向功能好吗？

高考试题具有数学测评、科研选题、命题示范、知识延展、思维训练、思想承载、教学导向和德育渗透等功能.［2］21题对2019年的复习备考有何启示呢？2019年的高考复习我们应何去何从？高三复习是否需要命制偏难怪试题？高三复习是否需要补充高等数学相关知识？等等.基于前文的分析，21题有引导高三复习补充高等数学知识之嫌，当然这与中学数学的教学实际不相符.同时，21题也有引导用偏难怪选拔人才之意，这与数年来高考选拔人才的方式相悖.

因此，21题第（Ⅱ）问不具备良好的导向功能.

三、对命制压轴题的一点思考

高考压轴题具有选拔功能无可厚非，但试题的难度不能肆意拔高，试题的背景理应公平，试题的立意不能脱离实际，试题应具有良好的导向功能.对此，我们认为命题应该做到以下几点：

首先，试题应该具有公平的背景，这是试题命制的前提，否则将失去考查的意义；其次，命制试题是一个严谨的过程，尤其是像高考这样的重大考试，试题及答案均应该精心打磨，不应出现争议；再次，试题的立意应该符合中学数学的教学实际，要具有良好的导向功能；最后，高考的选拔功能要适度，要切实有利于为高校选拔一批人才.

总之，高考压轴题——想说爱你不容易应是常态，而高考压轴题——想说爱你不可能应该杜绝.