对一道高考题的多解与变式研究
2019-05-29山东省临沂第一中学曹方瑜
☉山东省临沂第一中学 曹方瑜
圆锥曲线中椭圆与双曲线的离心率问题一直是一个热点,也是历年数学高考、竞赛中比较常见的一类问题,常考常新,变化较大.解决圆锥曲线的离心率问题的关键是寻找椭圆或双曲线中参数a、c所满足的关系式,根据题设条件可灵活利用圆锥曲线的定义与几何性质、解三角形知识或利用直线的方程、直线的斜率、平面几何性质等进行综合分析与处理,从而得以解决离心率的求值、离心率的取值范围等有关问题.
一、高考在线


题目 (2018·全国Ⅲ理·11)设F1,F2是双曲线的左,右焦点,O是坐标原点.过F作C的2一条渐近线的垂线,垂足为P,若则C的离心率为( ).
分析:根据题目条件,利用双曲线中参数a,b,c的几何意义可知可得,进而可以利用解三角形来建立参数a、c之间的关系式,也可以借助解析几何中直线的方程来转化,从而得以求解.
二、多维角度
对于双曲线问题,可以从多角度切入进行深度挖掘,从而达到触类旁通、一题多解的效果.不同的切入点有不同的解法,多点思维,多向开花.
解法1:如图1,由a,b,c的几何意义可知|OF2|=c,|PF2|=b,可得|OP|=a,而cos∠POF1=cos(π-
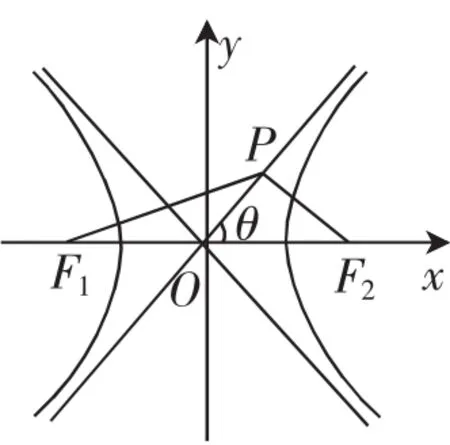
图1

故选C.
解法2:由a,b,c的几何意义可知|OF2|=c,|PF2|=b,可得|OP|=a,而
整理可得4c2-6a2=3b2=3(c2-a2),
即c2=3a2,
所以双曲线C的离心率为
故选C.
解法3:由a,b,c的几何意义可知,|OF2|=c,|PF2|=b,可得
由双曲线知其渐近线OP的方程为
整理可得c2=3a2,
所以双曲线C的离心率为
故选C.
三、变式拓展
当我们解完一道题之后,要不断地领悟反思,通过对该题的深入观察,拓展思维,改变条件,可以得到意想不到的效果.
变式1:设F1,F2是双曲线的左,右焦点,O是坐标原点,过F2作双曲线C的一条渐近线的垂线,垂足为P,若|PF1|=2|PF2|,则双曲线C的离心率为______.
解析:由a,b,c的几何意义可知|OF2|=c,|PF2|=b,可得|PF1|=2|PF2|=2b,
由双曲线知其渐近线OP的方程为
则直线PF2的方程为
所以双曲线C的离心率为
变式2:已知F为双曲线的右焦点,过点F向C的一条渐近线引垂线,垂足为A,交另一条渐近线于点B,若|OF|=|OB|,则双曲线C的离心率是( ).

解析:设双曲线的一条渐近线方程为则直线
AB的方程为
联立
则点A的坐标为
联立
解得
则点B的坐标为
由|OF|=|OB|知△OFB为等腰三角形,
则A为FB的中点,
则结合比例关系知,点B到x轴的距离为点A到x轴的距离的2倍,即
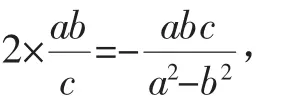
整理可得b2=3a2,
故选D.
变式3:如图2所示,已知F为双曲线的右焦点,过F作C的一条渐近线的垂线,垂足为M,延长FM与y轴交于点P,且|FM|=4|PM|,则双曲线C的离心率为______.
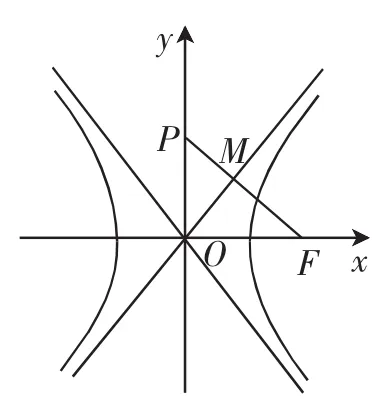
图2
解析:设F(c,0),则c2=a2+b2,由于双曲线1(a>0,b>0)的一条渐近线方程为
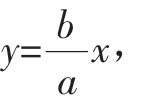
则垂线FM的斜率为那么直线FM的方程为
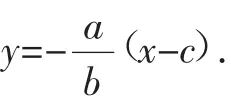
令x=0,得P的坐标

设M(x,y),由|FM|=4|PM|,
可得

即x-c=-4x且,解得
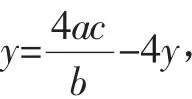


代,得

即4a2=b2,则有4a2=c2-a2,可得5a2=c2,
所以双曲线C的离心率为
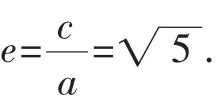
故填答案:

通过深入观察,多向思维,巧妙拓展,看似平常的一道圆锥曲线的离心率求解问题,却独具匠心,充分体现出命题者“以能力为主”“在知识网络的交汇点处设计试题”的命题理念.通过一题多变,培养了学生思维的应变性,实现了提高发散思维的变通性.把课本练习题、考题等通过变换条件,变换结论,变换命题等,使之变为更有价值、更有新意的新问题,从而应用更多的知识来解决问题,获得“一题多练”、“一题多得”的效果.F
