On the thixotropic effect of turbulence

Yu-Ning Huang*

State Key Laboratory for Turbulence and Complex Systems, College of Engineering, Peking University, Beijing 100871, China

Keywords:Second-order closure Natural viscosity of turbulence Launder, Reece and Rodi model Homogeneous isotropic turbulence Thixotropy

A B S T R A C T As a follow-up research of the work on the natural viscosity of turbulence of Huang et al. [Journal of Turbulence (2003)], here we investigate the thixotropic effect of a turbulent Newtonian fluid on the basis of the ensemble-averaged Navier–Stokes equation. In view of the natural viscosity, we show that in homogeneous isotropic turbulence the turbulent Newtonian fluid behaves like a thixotropic fluid, exhibiting the thixotropic effect with its natural viscosity decreasing with time.

A turbulent Newtonian fluid in many aspects behaves like a non-Newtonian fluid, exhibiting visco-elastic and memory effects as shown by Rivlin [1], Crow [2], Liepmann [3], Lumley [4],Builtjes [5], and Huang [6], among others. Thixotropy is a flowinduced phenomenon, which occurs in gels, emulsions, foods,coatings, and many other materials. Specific examples include milk, ink, paints, blood, and mayonnaise. The defining characteristic of a thixotropic fluid is the change in its material properties, such as viscosity and elasticity, with time under shear; see,for example, Mewis [7] and Barnes [8]. In this work, we shall focus on the thixotropic effect of a turbulent Newtonian fluid from the perspective of the natural viscosity of turbulence, in order to separate the natural viscosity of turbulence from the elastic effect of turbulence, noting that a study on the latter would be an interesting work on the normal-stress effect, i.e., the Weissenberg effect of turbulence [9, 10].

The natural viscosity is an intrinsic property of a fluid, as shown by Truesdell [11, 12] in 1964 and 1974. For instance, Lumley [13] mentioned that for a dilute polymer solution its viscosity is usually characterized by the zero-shear intrinsic viscosityfor simple shear flow, namely, the natural viscosity in the sense of Truesdell [11]. Therefore, to investigate the thixotropic effect of a turbulent Newtonian fluid, we can compare the natural viscosity of turbulence with the natural viscosities of the typical thixotropic fluids to show whether or not a turbulent Newtonian fluid behaves like a thixotropic fluid. To this end and for illustration,we shall seek an explicit expression for the natural viscosity of a turbulent Newtonian fluid based on the Reynolds stress transport equation. However, the Reynolds stress transport equation is not closed unless is modelled, and its closure equation, such as a second-order closure model, must be provided before any calculations to be performed. Here, we invoke the Launder,Reece and Rodi basic model of the second-order closure to derive an explicit expression for the natural viscosity of turbulence,noting that the Launder, Reece and Rodi model [14], which includes the model of Rotta [15] and the model of Naot, Shavit and Wolfshtein [16] as special cases, can describe well the return-toisotropy of turbulence.

Turbulence modelling, in its sense of modern times, had its beginning with Chou's paper [17] published in 1940 entitled “On an extension of Reynolds' method of finding apparent stress and the nature of turbulence,” as remarked by Lumley and Yaglom[18] in 2001 in their detailed, vivid and retrospective article on the studies of turbulence in the past century. Another seminal paper of Chou [19], entitled “On velocity correlations and the solutions of the equations of turbulent fluctuation” published in 1945, also made a remarkable contribution to the foundation of turbulence modelling on the basis of the ensemble-averaged Navier-Stokes equation and, in particular, the second-order(moment) closure for turbulence modelling, long before the advent of advanced and powerful modern computers and their practical applications in turbulence modelling; see, for example,Rotta [15], Launder, Reece and Rodi [14], Launder [20], Lumley and Yaglom [18], Girimaji [21]. Shortly after the work of Chou[19], Rotta [15] in 1951 first put forth a model for the slow pressure-strain correlation, which plays an important role in describing the return-to-isotropy behavior of turbulence. The further development and implementation of the second-order closure along this line of approach over the years have been clearly shown in the papers of Launder et al. [14], Naot et al. [16], Daly and Harlow [22], Donaldson [23] and in many others' research of the second-order closure [18, 20, 21, 24].

The so-called second-order closure is about closing the Reynolds stress transport equation by modelling the unknown terms that appear in it:

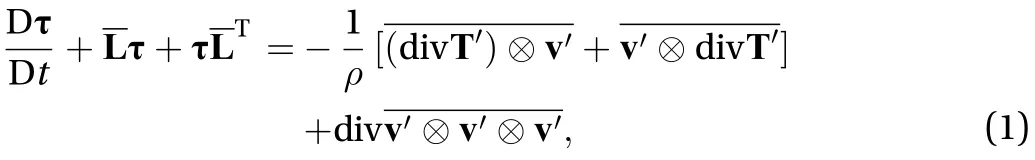
where an overbar represents the ensemble mean,denotes the material time derivative associated with the mean velocity field,is the mass density,is the Reynolds stress tensor in its kinematic form whereinis the fluctuating velocity,,in whichis the fluctuating pressure,is the unit tensor,is the viscosity, andis the fluctuating stretching tensor.

In what follows, we shall employ the Launder, Reece and Rodi [14] basic model of the second-order closure to derive an explicit expression for the natural viscosity of turbulence. By comparing the natural viscosity of turbulence with the natural viscosities of those typical thixotropic fluids, we shall show that in homogeneous isotropic turbulence a turbulent Newtonian fluid behaves like a thixotropic fluid with its natural viscosity decreasing with time.

Consider a homogeneous turbulent shear flow, in whichand, we have

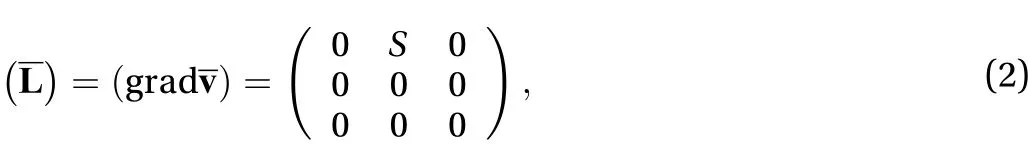
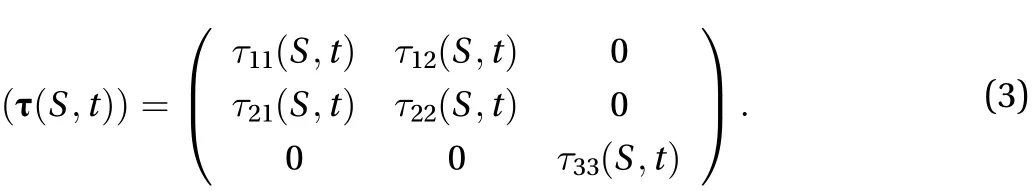
In a homogeneous turbulent shear flow, in the limit as the mean shear rate, the limitis the natural viscosity of turbulence in its kinematic form [25], which is in keeping with the concept of the natural viscosity introduced in 1964 by Truesdell [11] for simple fluids in a viscometric flow (see Ref. [12] for details) and therefore manifests itself through its existence corresponding to that of the non-Newtonian fluids.

For convenience in later discussion, we quote below two results concerning the natural viscosity of turbulencefrom the article of Huang et al. [25] published in 2003:

Theorem 1. In the limit of zero shear rate in homogeneous turbulent shear flow of a Navier-Stokes fluid, there exists the natural viscosity of turbulence which takes the form:

Theorem 2. The natural viscosity of turbulence of a Navier-Stokes fluid is always non-negative, i.e.,.

As we shall see, as a mathematical measure depicted in the above two theorems, the exact solution to the natural viscosity of turbulence, which we are going to derive by using the basic model of the second-order closure, actually describes the decaying homogeneous isotropic turbulence in a way different from the turbulent kinetic energyand the turbulent dissipation ratein that regard, as clearly expressed in Eq. (4).

In homogeneous turbulence, the Reynolds stress transport equation (1) reduces to

The basic model of the second-order closure adopted here is the first of the two models proposed in 1975 by Launder, Reece and Rodi [14], which includes both the model of Rotta [15] and the model for isotropization of production proposed by Naot,Shavit and Wolfshtein [16]. That is, the Launder, Reece and Rodi model for the pressure-strain correlation tensortakes the following form:

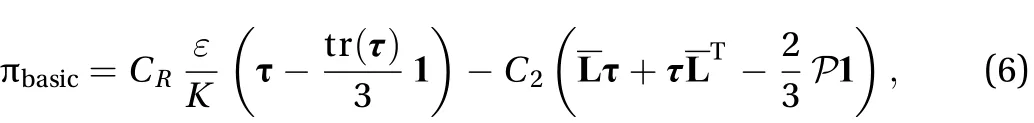
and at high Reynolds number:

Now for a homogeneous turbulent shear flow, the shear stressin the Reynolds stress transport equation, in conjunction with the Launder, Reece and Rodi basic model of the second-order closure Eqs. (6) and (7), takes the following form:

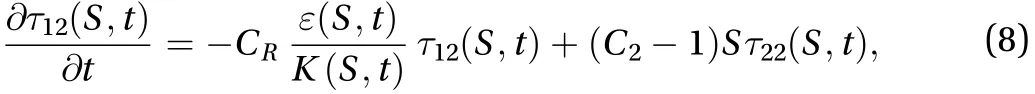
We rewrite Eq. (8) as

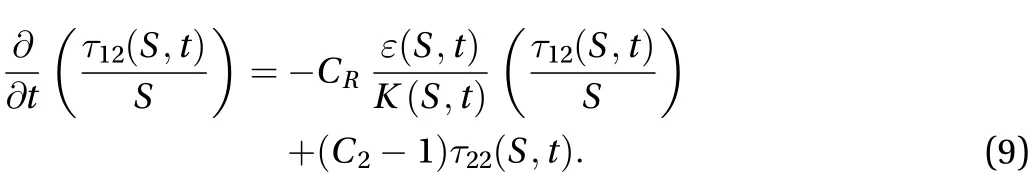
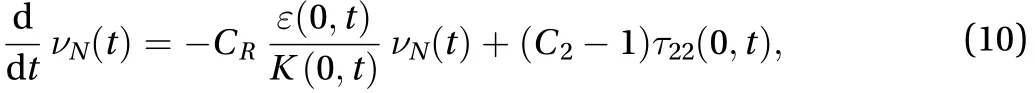
Note that in the limit of zero mean shear rate (), a homogeneous turbulent shear flow becomes homogeneous isotropic, therefore

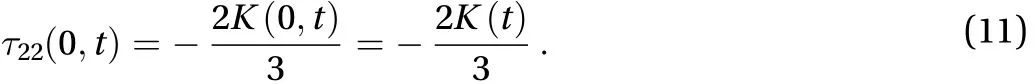
Thus, Eq. (10) becomes

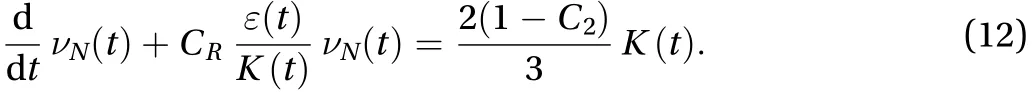
Moreover, the turbulent kinetic energydecays as

and the turbulent dissipation rate

Since in homogeneous isotropic turbule nce

Substituting the above decay laws into Eq. (12) gives

Hence, by integration, we obtain the following exact solution to Eq. (16):

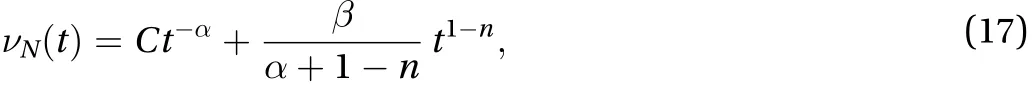
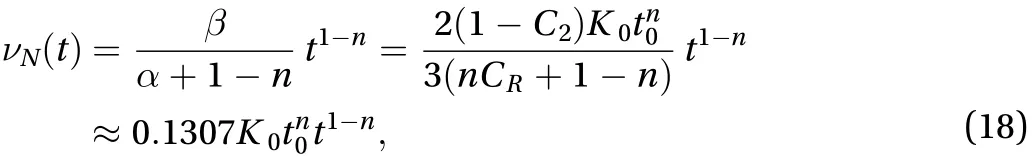
which is always non-negative, as shown by Theorem 2.

It has been shown in the article of Huang et al. [25] that the standard-model and the non-linear-model of Speziale yield the same value of the natural viscosity of turbulence:

Clearly, Eqs. (18) and (19) predict the same decaying trend asfor the natural viscosity of turbulence.

The above results indicate that the natural viscosity of turbulence predicted by the standard-model and the non-linear-model of Speziale, i.e.,, confirms pretty well with Eq. (18), which is merely a special solution of the natural viscosity of turbulence Eq. (17). Moreover, interestingly, in Eq.(17), the first termthat is due to Rotta's model decays as, much faster than does the second term withthat is due to the model for isotropization of production. That is, in view of Eq. (6) and Eq. (17), Rotta's model plays a significant role in modifying the prediction yielded by the model for isotropization of production.

It is evident from Eq. (17) that the integral constantcan be readily identified, provided thatbe given by relevant experiment or direct numerical simulation, noting again that, and atthe homogeneous isotropic turbulence starts to decay. Hence, there follows

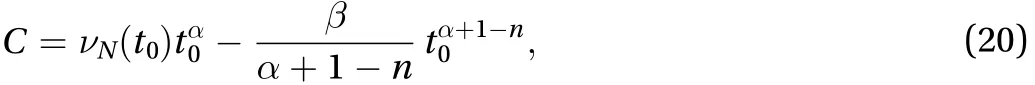
Finally, the exact solution to the natural viscosity of turbulence based on the Launder, Reece and Rodi basic model reads

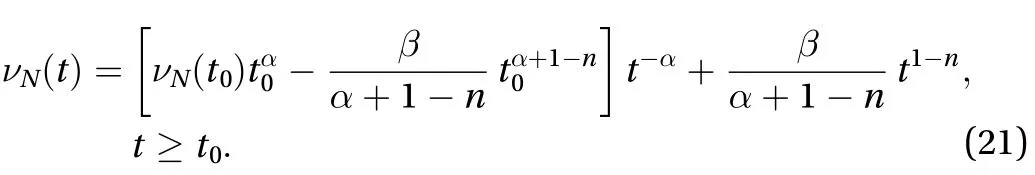
Here, we shall study the thixotropic effect of the turbulence of a Newtonian fluid. The rheological phenomenon of thixotropy is a manifestation of flow-induced microstructural changes of the fluid, which may be observed in colloidal systems such as cross-linked gels, emulsions, foods, biological systems, clays,coatings, and others. The best known examples of thixotropy are probably clay suspensions. On standing a clay suspension becomes a gel, but when being shaken it behaves like water. The main characteristics of thixotropic fluids are the change in material properties, such as viscosity and elasticity, with time due to shearing [8, 28]). Although in history there existed various definitions, nowadays, the definition of thixotropy essentially asserts that the viscosity is time-dependent, decreasing with time.

In the summary of their 2009 article on thixotropy, Mewis and Wagner [28] concluded: “For a wide range of colloidal suspensions the viscosity is not only a function of shear rate but also of time.” Therefore, in simple shearing flow, let the shear rate in the viscosity of a thixotropic fluid concerned go to zero we then obtain its natural viscosity in the sense of Truesdell [11, 12]. And by adopting the natural viscosity we can examine the time-dependent behavior of thixotropy [7], noting that for thixotropic materials that exhibit both thixotropic and viscoelastic effects,there had been confusion between thixotropy and shear-thinning, as had been documented in the literature of thixotropy. In fact, it is very difficult to accurately determine the physical properties of a complex fluid. For instance, sometimes, it is hard to determine whether an observed non-Newtonian effect is caused by shear-thinning, elasticity or both. But, the Boger fluid, an elastic dilute polymer solution with a constant viscosity, has an interesting feature that enables elastic effects to be clearly separated from viscous effects [29].

To investigate the thixotropic effect of a turbulent Newtonian fluid, let us start with identifying the natural viscosities of the following Newtonian and Non-Newtonian fluids respectively,which are the intrinsic properties of the fluids in question, of course.

(a) For an incompressible Newtonian fluid, we have the following constitutive equation

Substituting the above constitutive equation into Cauchy's first law of motion

in which an overbar represents the ensemble average,denotes the material time derivative associated with the mean velocity fieldis the mean pressure,is the mean stretching tensor, andis the Reynolds stress tensor in its kinematic form,whereis the fluctuating velocity.

In homogeneous turbulent shear flow, the mean stretching tensorin Cartesian coordinates,whereis the mean shear rate. Now, in view of the above ensemble-averaged Navier-Stokes equation, the shear viscosity function (viscometric function [25]) of a turbulent incompressible Newtonian fluid reads

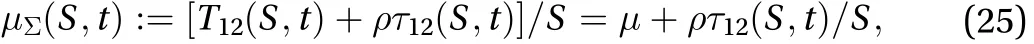
to which both the mean Cauchy shear stressand the Reynolds shear stresscontribute respectively.

Hence, in the limit of zero mean shear rate, it is clear that the natural viscosity of a turbulent incompressible Newtonian fluid is

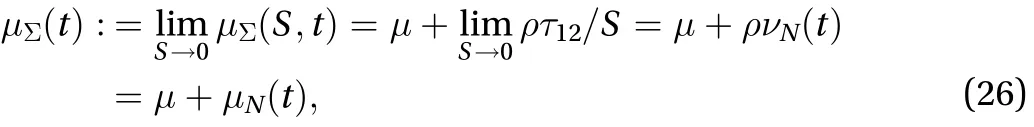
(b) Let us consider an incompressible Reiner-Rivlin fluid,noting that many geological, biological materials, food products and chemicals may be adequately described by the Reiner-Rivlin constitutive equation

In simple shearing flow, the stretching tensorin Cartesian coordinates, whereis the rate of shear. Here, the shear viscosity function (viscometric function)

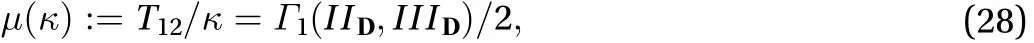
which is a function of the rate of shearand time-independent,capable of modelling shear-thinning.

In the limit of zero shear rate, it is straightforward to show that the natural viscosity of the Reiner-Rivlin fluid reads as

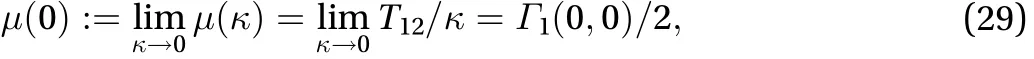
which is a material constant.

(c) Consider one more example, the incompressible fluid of grade 2, which can predict the normal stress (elastic) effect, also known as the Weissenberg effect:

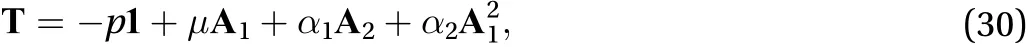
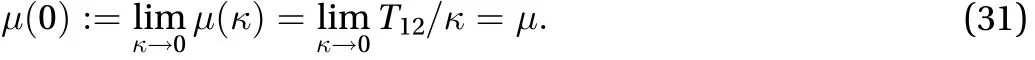
To calculate the natural viscosity of a thixotropic fluid, which is not a material constant but a time-dependent material coefficient, let us have a look in depth at the following typical thixotropy models.

(I) A typical model of thixotropy proposed in the approach of continuum mechanics [28]:

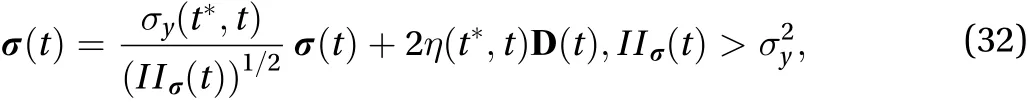
In simple shearing flow where the stretching tensor, from Eq. (32) there follows at once the natural viscosity in the limit of zero shear rate:

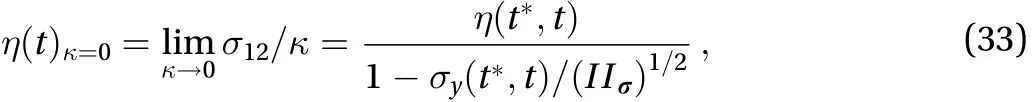
which is time-dependent, involving the history of the flow concerned.

(II) In the so-called structural kinetics approach, the non-linear time-dependent behavior of a thixotropic fluid can be described by a set of two equations [7]. For the stress tensor:

By the representation theorem [30-32], Eq. (34) is readily expressed to be

So, in simple shearing flow where the stretching tensor, from Eq. (36) there follows readily the natural viscosity in the limit of zero shear rate:

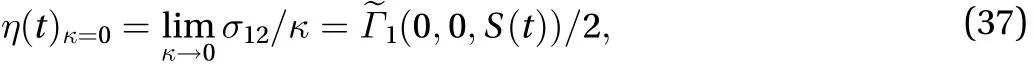
which is simply time-dependent, with the structural parametersatisfying the kinetic equation:

where the constitutive functionis to be specified according to the underlying rheological structures of the thixotropic materials. This approach has been successfully applied to the rheology of dilute dispersions in which the microstructure is well understood, and has now been advocated for the modelling of larger classes of materials [7].

A rather general form for the shear stressthat is compatible with the above Eqs. (34) and (35) is given by the following set of equations [7]:

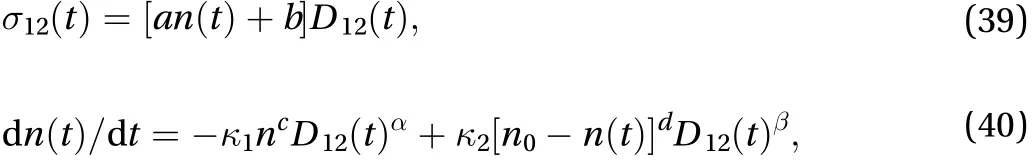
Therefore, the corresponding natural viscosity in the limit of zero shear rate is:

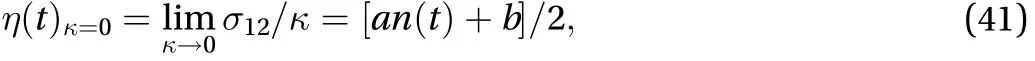
which is time-dependent withbeing described by Eq. (40).

(III) Moreover, to model the typical thixotropic behavior, experimenters place a thixotropic material into a viscometer and apply a constant shear rate to find that the measured shear viscosity will decrease with time, but it will eventually steady out to a constant value [8]. Here the so-called stretched exponential model is often used to characterize the typical response to a step-wise change from one steady state condition to another,and its natural viscosity decreases gradually with time and takes the form:

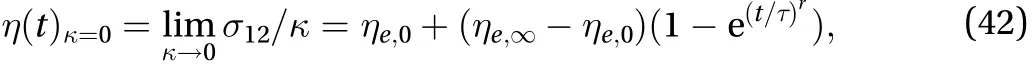
Now we are ready to compare the natural viscosity of turbulencewith the natural viscositiesof the above typical thixotropic fluids. By Theorem 1 in the paper of Huang et al.[25], we know that, in the limit of zero shear rate in homogeneous turbulent shear flow of a Navier-Stokes fluid, there exists the kinematic natural viscosity of turbulence:

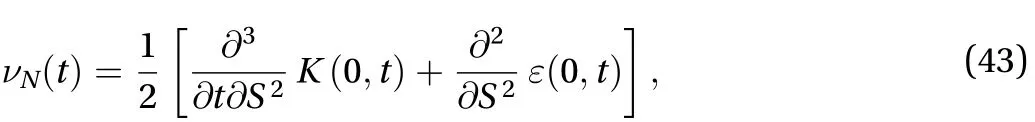
which is simply time-dependent; and, because as timegoes to,and, consequently, the homogeneous isotropic turbulent Newtonian fluid resumes a laminar Newtonian fluid.

And the expression for the kinematic natural viscosity of turbulence given by the Launder, Reece and Rodi basic model of the second-order closure reads

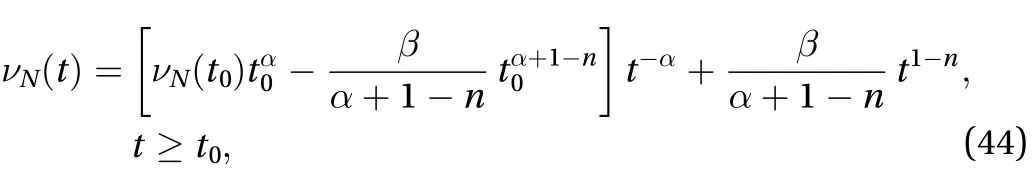
On comparing the natural viscosityof a turbulent Newtonian fluid, i.e., Eq. (26), with the natural viscositiesof the thixotropic fluids derived respectively in cases (I), (II), and(III), it is clearly evident that, in homogeneous isotropic turbulence, the turbulent Newtonian fluid behaves like a thixotropic fluid, exhibiting the thixotropic effect with its natural viscosity decreasing with time.

Indeed, by Eqs. (26) and (43), we find that, like the natural viscosityexpressed in Eq. (42) for a typical thixotropic fluid,in whichand,the natural viscosity of a turbulent Newtonian fluidbears a striking similarity towith its defining characteristic:

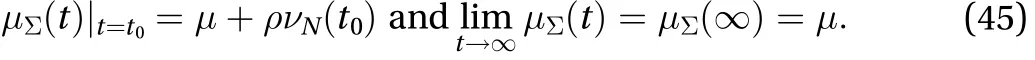
Moreover, this interesting fact may be properly illustrated by Eq. (44) derived from Launder, Reece and Rodi's basic model,here

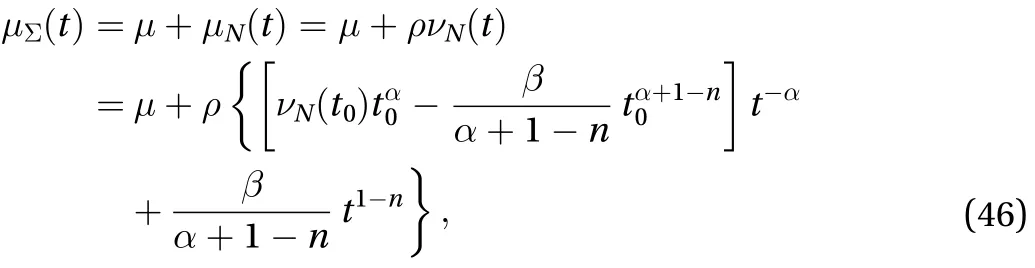
Following the line of thought of Rivlin [1] which suggested that some analogy may exist between the turbulent Newtonian fluid and the laminar flow of a non-Newtonian fluid, in this paper we have investigated the thixotropic effect of a turbulent Newtonian fluid in homogeneous isotropic turbulence. The existence of the natural viscosity of turbulence is a manifestation of the thixotropic effect of the turbulent Newtonian fluid, as exemplified by the expression for the natural viscosity of turbulence given by the Launder, Reece and Rodi basic model of the second-order closure.

In fact, showing that there exists thixotropic effect of turbulence is the first and vital effort towards modelling it, because without knowing its existence in the first place it is impossible to describe this interesting phenomenon, let alone make any prediction of it.

The natural viscosity of turbulence is not only a measure for the decaying homogeneous isotropic turbulence, such as the turbulent kinetic energyand the turbulent dissipation rate,but also in turbulence modelling at large, it can serve, using its DNS results, to examine the second-order closure models, the non-linear-models and the approach of large eddy simulation of their accuracy in predicting the natural viscosity of turbulence--a property of turbulence that is directly derived from the Reynolds stress transport equation per se. Therefore, it will be of interest to carry out experiment and direct numerical simulation [33] for the evolution of the natural viscosity of turbulencein great depth in the near, or perhaps, in the foreseeable future.