Numerical solutions for point masses sliding over analytical surfaces: Part 2
2019-05-28StefanoTintiGlaucoGallotti
Stefano Tinti, Glauco Gallotti*
Department of Physics and Astronomy, University of Bologna, Bologna 40126, Italy
Keywords:Two-point system Rigid-body motion Sliding downslopes
A B S T R A C T This paper is the second of two companion papers addressing the dynamics of two coupled masses sliding on analytical surfaces and interacting with one another. The motion occurs under the effect of gravity, the reaction force of the surface and basal friction. The interaction force maintains the masses at a fixed distance and lies on the line connecting them. The equations of motion form a system of ordinary differential equations that are solved through a fourth-order Runge–Kutta numerical scheme. In the first paper we considered an approximate method holding when the line joining the masses is almost tangent to the surface at the instant mass positions. In this second paper we provide a general solution. Firstly, we present special cases in which the system has exact solutions. Second, we consider a series of numerical examples where the interest is focused on the trajectories of the masses and on the intensity and changes of the interaction force.
1 Introduction
This paper is an extension of the study in Ref. [1]. More precisely, we present a system of ordinary differential equations(ODEs) that describes the motion of a couple of masses sliding down analytical surfaces and interacting with one another. The forces that act on the system are gravity, the reaction force of the surface, friction and the interaction force. This latter represents the core of this study and is widely analyzed to see how it depends on the slope geometries and on the system dynamics.
Following the formulation [1] the equations are built under the assumptions that the masses are strictly adherent to the surface and cannot leap or jump from the surface itself. In all simulations, we use surfaces described by equations of the type z =f (x, y), where z represents the vertical coordinate in a Cartesian reference system, and x, y are the coordinates in a horizontal plane.
In the previous paper we considered an approximated system where the projections of the interaction forces in the direction normal to the surface were neglected, which was acceptable for the surface geometries taken into account there. In this paper, we deal with the full system of equations. In the next section, we present the new theoretical approach. Then we treat simple no-friction analytical cases. Finally, we show and discuss further cases where masses move in a very complicated way,mainly due to the presence of the interaction force. The twomass system considered here is a very simple structure. The extension to a more complex structure formed by a large number of interacting masses is one of the objectives of our research, but as a first step, it requires the full understanding of the dynamics of the basic system we describe here. In this paper, we do not focus on the choice of the numerical method used to solve the equations. As seen in Ref. [1], a fourth-order Runge–Kutta scheme (RK4) provides satisfactory results in terms of computational efforts and accuracy and hence we use it throughout this paper.
In the following examples, the initial conditions of the systems are given in terms of positions and velocities values. In this paper we are interested to the dynamic evolution of the systems.Therefore, when we present cases of systems initially at rest, we restrict to systems that, being not in equilibrium, start moving.Addressing cases of stable systems, where system can move as the result of destabilizing mechanisms, is not within the scope of this paper and will be the object of future research and fully described in upcoming works.
2 Formulation of the problem
We assume that two point-like particles with masses m1and m2are initially in the positions P1(x1, y1, z1) and P2(x2, y2, z2) on the surface z = f (x, y), in a Cartesian reference system where x and y are the horizontal coordinates and z is the vertical one. As seen in Ref. [1], the equations of motion for a couple of interacting particles sliding down a smooth surface are

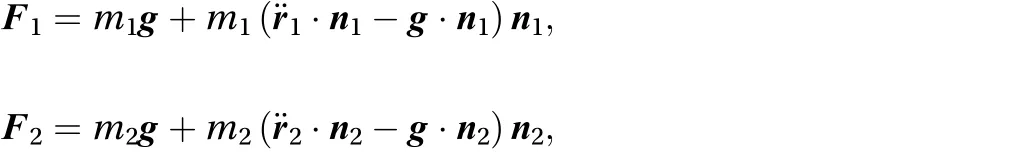
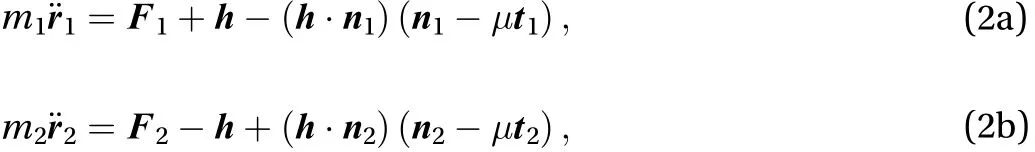
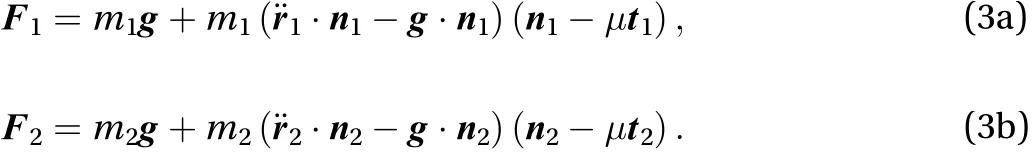
Considering that the forcesinclude terms depending on the position of the masses and on the centripetal accelerations,that in turn can be written in terms of curvature radiuses Riand of velocities (see Appendix A1), we can isolate the mass accelerations in the first member of Eq. (2) and write
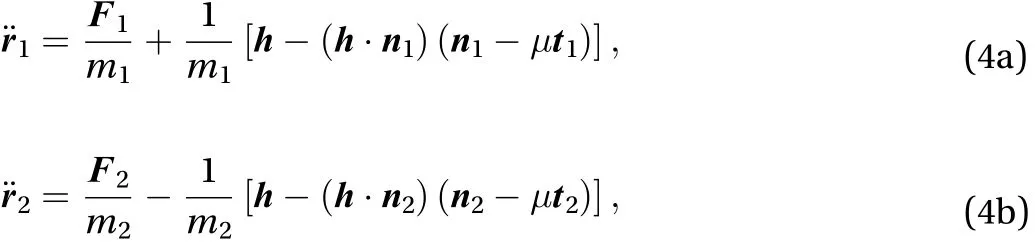
where the forces are given by Eq. (3). The interaction force we consider here is such that the distance between the masses is constant, which means that the joining vectorhas a constant magnitude. Imposing this constraint in the way given in detail in Appendix A1, and assuming that the forcepoints towards the same direction as direction

We can obtain the following expression for the interaction force
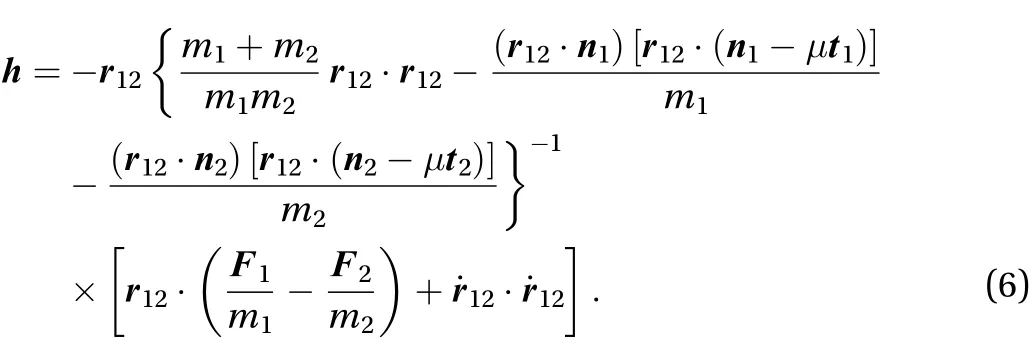


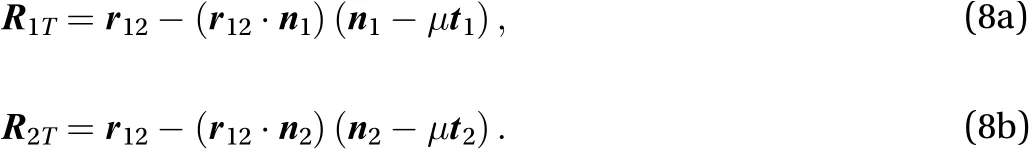
Considering Eqs. (2), (7), and (8), we can write the equations of motion for the various components in the form

If we introduce the arrays p and b such that

The system of Eq. (9) can be written in the compact form

where A is a 4×4 diagonal matrix with: A11= m1, A22= m1, A33=m2, A44= m2. Eventually, Eq. (12) can be turned into a system of first-order differential equations as

Equation (13) is suitable for solution searched by means of Runge–Kutta numerical methods. More precisely, we use RK4,which was shown to be satisfactorily accurate for this kind of problems [1].
3 Analytical solutions
The theory just described is first tested through cases admitting an analytical solution for the motion of the two-mass system. These solutions allow us to find an exact form for the interaction force given in Eq. (6).
3.1 Case 1
The first case we propose is a constant velocity circular motion on a concave sphere described in a Cartesian reference system by the equation
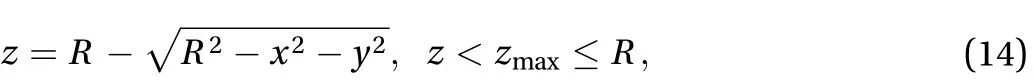
where R is the sphere radius.
As seen in Ref. [1] a particle on a spherical surface moves along a horizontal circular trajectory, if it is posed at a distancefrom the vertical axis and pushed with an initial horizontal velocity v0equal to

Here, we impose that the two masses have initial velocities given by Eq. (15), are initially placed on a horizontal circumference of radius r and are separated by the angular shift.
Under these conditions, we expect that, independently from the choice of, the particles will spin on the same plane keeping their initial velocities and shift constant over time. The equations for the displacement components are given by

We set up a simulation case where we take a spherical unitradius surface and two equal masses (m1= m2= m) at the initial positionsand, with=23.6° and the phase shift. The initial velocities are correspondingly set toand, with v0evaluated through Eq. (15). We run the numerical simulations for t = 5T, whereis the motion period. The difference of the numerical and analytical solution is found to be very small. For example,the discrepancy for horizontal displacement x(t) normalized over the motion radius r results to be confined to the order of 10–9). Likewise, from our computations the interaction force normalized over mg turns out to be in the range of 10–13) which is practically zero, as it should be.
The second case we propose regards a system of particles on a sphere where the interaction differs from zero. We set the masses m1and m2at different heights on the sphere in the same vertical plane. With no loss of generalization, we take the initial horizontal positions inand.It can be shown that the masses move uniformly on the circles respectively of radiusand, if their initial velocities areand, with v1and v2satisfying the expressions
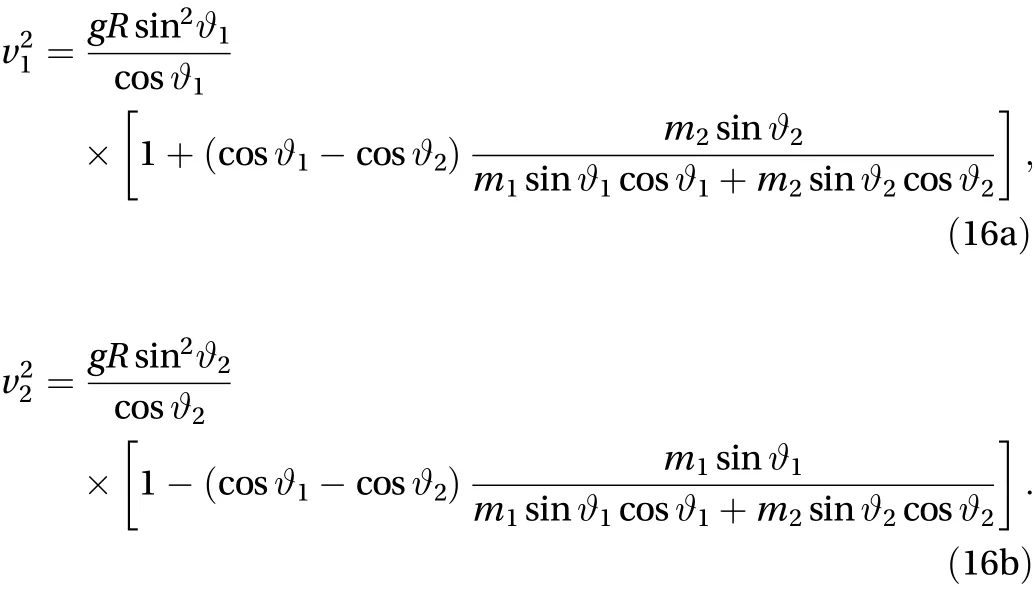
It is worth pointing out that the masses have the same angular velocity, given by

The analytical solution for the motion of the masses is

It can be shown that the interaction force has a constant magnitude given by the following exact expression
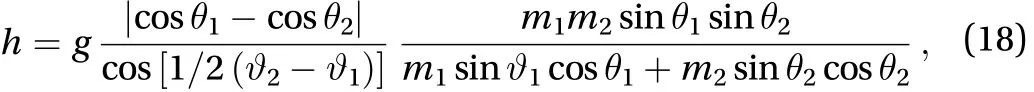
where h is defined in Eq. (4). It is worth observing that h does not depend on the sphere radius R. Notice further that if one of the two masses is set at the bottom of the sphere (for example if), the mass does not move, while the other one spins as it were free, with v2taking the form seen in Eq. (15).
In Fig. 1 we display the values of h given by Eq. (18), in the case of two equal masses (m1= m2= m) normalized to mg, as a function ofand. In virtue of its definition given by Eq. (4),when h is positive, it means that mass 1 is pushed away by mass 2 (rejected), which is a reciprocal action. In our case, h as given by Eq. (18) is always positive, and hence the interaction is repulsive in character. To explain this, one should consider that mass 1 rotates at a speed higher than the corresponding free particle. A free particle with the same speed would then tend to move outward from the rotation axis and therefore to climb up to higher values of z. Likewise, the upper mass, if free, would tend to move downward. The interaction force opposes this trend and keeps them at their own level pushing them away from one other. Looking at the contour plot of Fig. 2, one sees that, on the bisecting line where, the magnitude of h is zero, because the two-mass system degenerates to a single mass.Expectedly, the plot is symmetric with respect to the bisecting line.
Notice that h results to be a multivalued function in the nodes (,) and (,), where its value ranges from 0 to. Also in the node (,), it is undefined and takes on values in the range from 0 to mg. Figure 3 shows the contour plot of h for a two different-mass system.The masses are m1= (1–k)m and m2= (1+k)m, where m is the average mass and k is the mass unbalance coefficient. Looking at the graph, one can see that the bisecting line is still a locus of zero values, but not a symmetry line. It can be shown that in the bottom right corner the function values range from 0 to, in the upper right corner they are in the interval from 0 to, while in the upper left corner the interval of variation is between 0 and
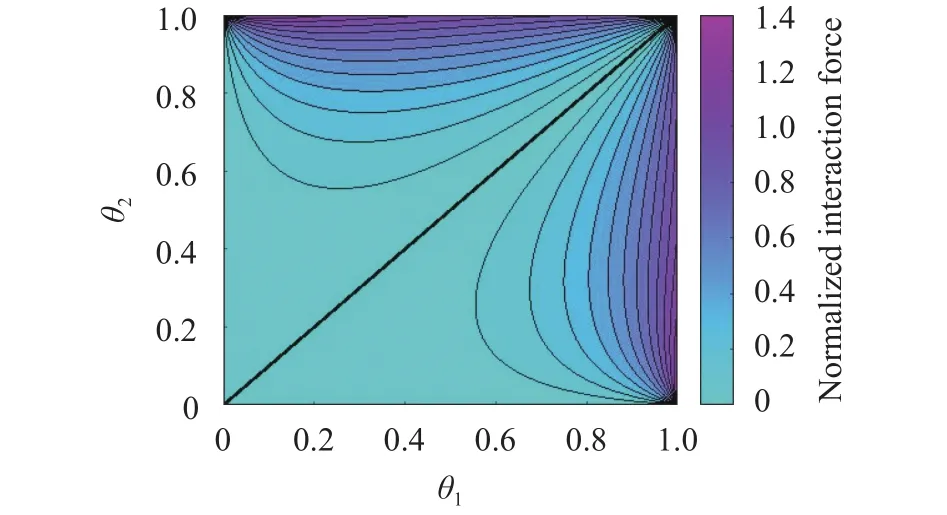
Fig. 1. Interaction force between two equal masses spinning at different heights on a sphere, normalized over mg, as a function of the angles and in the range from 0 to. The angles are measured in units. The contour lines are spaced by 0.1. The black thick line represents the bisecting line where h is zero.
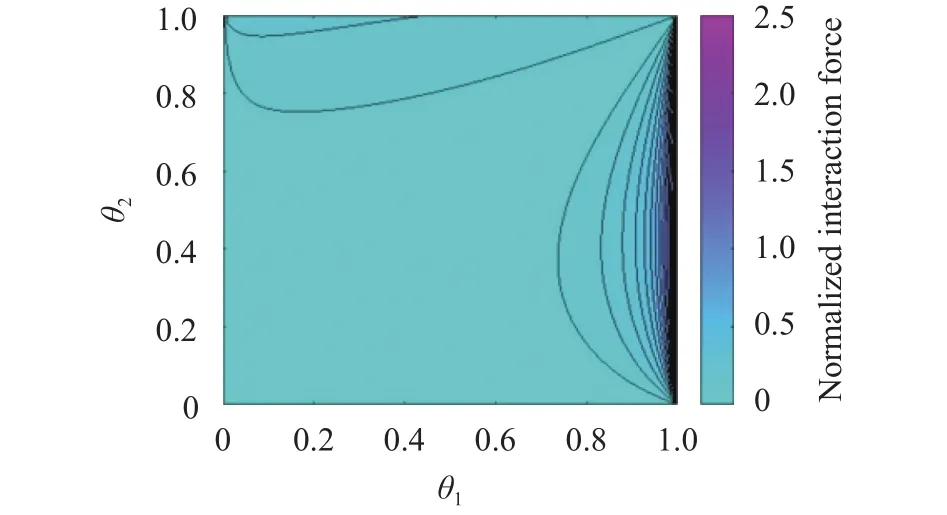
Fig. 2. Interaction force between two different masses spinning at different heights on a sphere, normalized to mg, where m is the average mass of the particles (unbalance coefficient k = 0.82). Anglesand are measured in units. The contour lines are spaced by 0.1.
Fig. 3. Period estimated through Eq. (21), scaled top as a function of the initial colatitude and longitude of the masses. Angles are in the range from 0 to and are measured in units.
In the numerical simulations, we suppose the initial horizontal positions of the two equal masses inandon a unit-radius sphere with= 17.5° and=23.6°. According to Eq. (17), the period of rotation around the vertical axis is slightly larger (by a factor 7 × 10–3) than the corresponding period of the free particle 2 (see the previous example).From Eq. (18), the interaction force turns out to be quite weak,having the value h/mg = 6.9 × 10–3. We compute the numerical solution for t = 5T, where.
The differences between the numerical and analytical positions on the x-axis, i.e. x(t), normalized to the radiuses of the circular motion, are in the order of 10–6. Furthermore, the difference between the interaction force estimated through the RK4 scheme and the analytical expression Eq. (18) are in the range of 10–3, which suggests that the RK4 scheme provides satisfactory results.
3.2 Case 2
The next theoretical case is the motion of two equal masses that start from rest on a spherical surface from the same height.Let's suppose that m1= m2= m, and that the initial positions on the sphere can be described by the colatitudeand the longitudeas follows
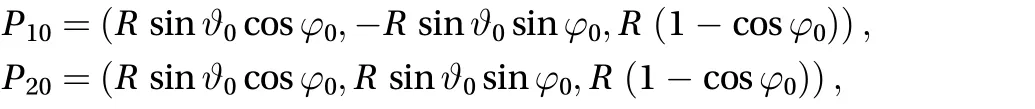
where R is the radius. Due to the perfect symmetry of the problem with the respect to the vertical plane y = 0, we expect that the two masses have equal colatitudeand opposite longitudeat any time. This means that the instantaneous position of the two masses are
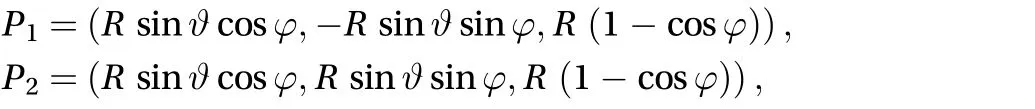
and their distance is

Since d does not change in time, it implies that the productis a constant of the system motion.
The center of mass (CoM) of this system has the position
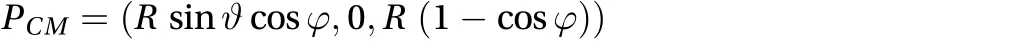
and its distance from the sphere center is. Because the product of the sinuses is a motion constant, it follows that during the motion the CoM moves on an arc of radius RCM. If we callthe angle formed by the radius RCMwith the vertical axis at the time t, we can use it as a coordinate describing the instantaneous position of the CoM.It is easy to see that the link betweenand the colatitudeis

Considering that only the gravity forces contribute to the momentum calculated with respect to the center of the sphere, it can be shown that the CoM dynamics is governed by the pendulum equation

which is cyclic with a period equal to
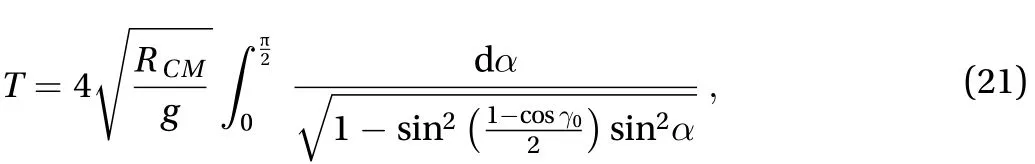

and the coordinates of the masses are
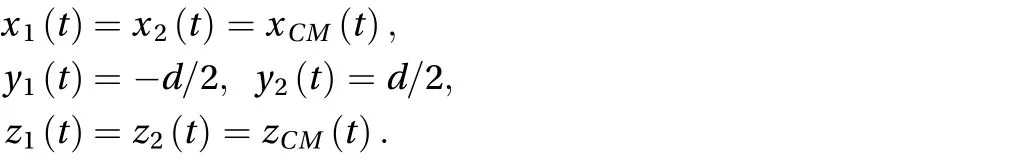
The interaction force calculated through the Eq. (5) can be written as

In terms of colatitude and longitude, the above expression turns out to be
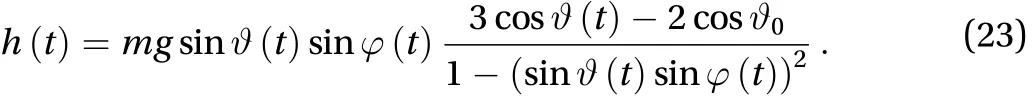
The solution of the problem can only be found numerically by solving Eq. (20) providing, and then using the geometrical relation Eq. (19) and the invariance of the distance d to findand. There are, however, some properties that can be deduced analytically. For example, the interactive repulsive force h(t) oscillates between a minimum and maximum value that can be written as
One can observe that h does not depend on the radius R, and scales as mg. In Fig. 4 we show contour plot of hmax/(mg) as a function of the initial colatitude and longitude of the masses.The plot suggests that hmaxgrows larger and larger whenandapproach, and provides an example where the interaction force can largely dominate on the weight of the masses.
The numerical solution of the Eq. (20) has been computed through an RK4 scheme. It is taken here as the reference solution against which we compare the solutions of Eq. (13) for the coupled system. On a unit-radius sphere, we select the colatitude= 24.35° and the longitude= 14.04°.
Initial velocities are set to zero. The oscillation period estimated through Eq. (21) and by the numerical solution of the coupled system leads to almost the same value with a relative error in the order of 10-5. Computations are carried out for 5 periods.
The absolute differences between the values of x(t) computed numerically and analytically, normalized to RCM, are equal for both masses, in the order of 10-12. The interaction force h oscillates between the values 0.092mg and 0.118mg, as it is clear in Fig. 5 where the time history of the interaction force of the numerical solutions is shown. Differences between the numerical and analytical solutions are very small, in the order of 10-12.
The previous case is also treated considering the presence of the friction force acting on the system. In this case, the CoM dynamics is represented by the equation
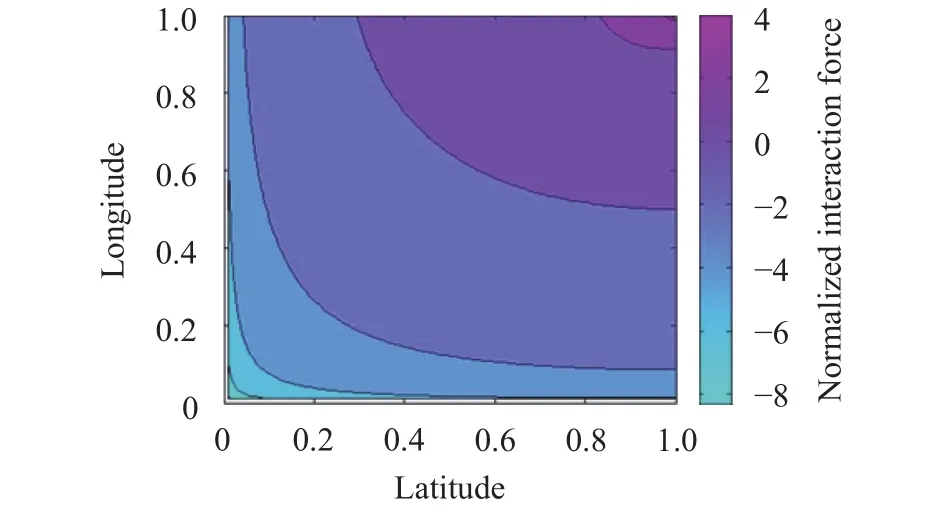
Fig. 4. Maximum interaction force (in logarithmic scale) for two equal masses oscillating in parallel and at same height on a sphere,scaled to mg, as a function of initial colatitude and longitude. Angles are in the range from 0 to and are measured in units.
The interaction force is independent of basal friction but depends on the particles velocities. Hence, its general trend is not given by Eq. (23) since we expect h to decrease as the particles decelerate under the effect of friction. The minimum value is still given analytically by Eq. (24), as in the frictionless case, but the maximum value depends on the maximum velocity value that can be obtained only numerically. When the modulus of the particles velocities reaches the minimum, the interaction force becomes constant and is given by

To illustrate this case we set the masses at the same initial positions as for the no-friction example and we use a friction coefficient. We obtain differences between the x(t) of 10-2, proving a loss of accuracy of the numerical methods with the presence of a dissipative force such as basal friction. The interaction force variations vs. time estimated through the numerical solutions are shown in Fig. 6. As can be easily noticed the first oscillation is similar to the no-friction case since the velocities are quite similar. As the effect of damping becomes more evident, the interaction force clearly decreases reaching a constant value when the particles velocities are close to zero. The differences between the reference and numerical solutions are in the order of 10-3.
4 Numerical solutions
Analytical solutions for the two-mass problem can be found only in very special cases. In this section we consider a series of problems admitting only numerical solutions with the purpose of getting some hints on the interaction force and on how it influences the system dynamics.
4.1 Example 1
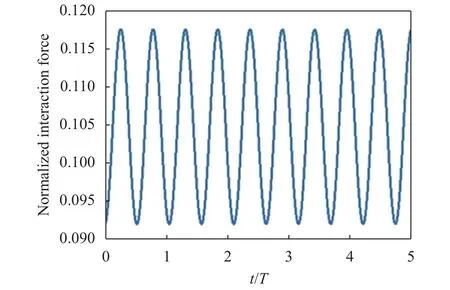
Fig. 5. Interaction force, normalized to mg, vs. time for the numerical solution of the coupled masses problem.
First examples are variants of the case we proposed in the previous section: a pair of equal masses initially set at the same longitude on a unit-radius sphere with initial velocities given by Eq. (16). Here we consider the effect of friction. We take the colatitudes as= 17.5° and= 23.6°, and compute the solution for t = 5T, where T is the rotation period of frictionless masses.We show the mass trajectories in Fig. 7 when the friction coefficient is set to. Friction decelerates the particles that are not able to keep the initial colatitude but tend to move towards lower heights.
We analyze the trend of the interaction force when the friction coefficientis increased from zero to. For the frictionless case, the interaction force h is constant in time and given by Eq. (18). From Fig. 8 one can observe that, when friction is active, h tends to increase with time. The reason is that since masses loose longitudinal speed, the interaction force has to balance the fraction of the mass weight that is not balanced by the sphere surface. It can be shown that, if the masses are initially separated by the angle, the equilibrium value for h when the masses are eventually at rest is given by. For the case treated here, this limiting value turns out to be h =0.053mg. Figure 8 shows that h tends to attain this value more rapidly for higher friction coefficients.
4.2 Example 2
The next example is a complex motion over an elliptic para-boloid. The bottom surface is described by the equation
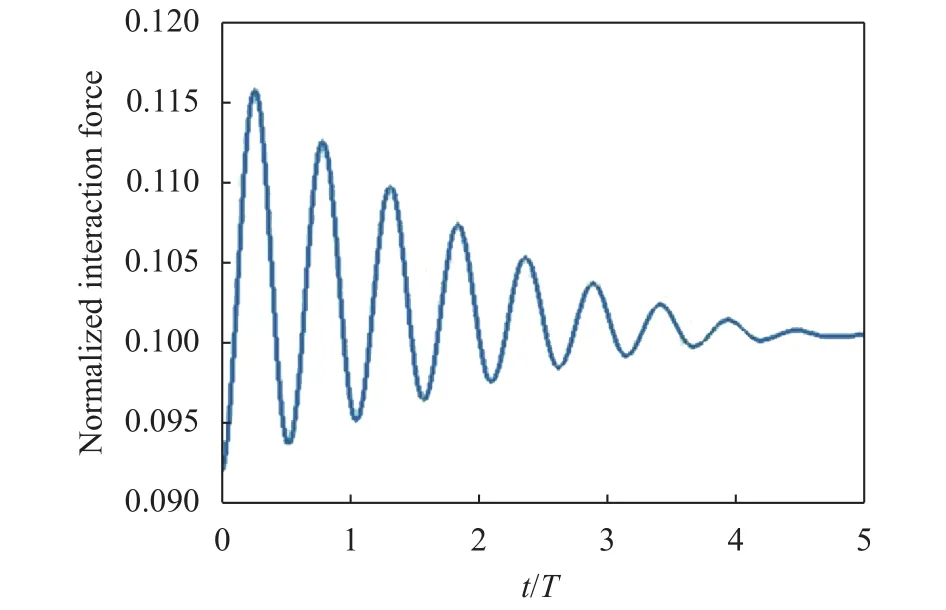
Fig. 6. Interaction force, scaled to mg, vs. time for the numerical solution of the coupled masses moving on a rough surface().
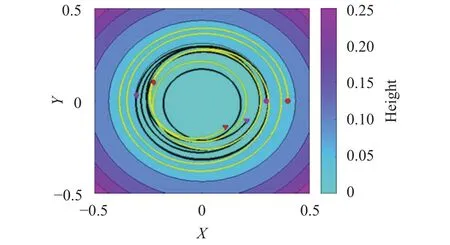
Fig. 7. Trajectories (yellow and black) for two equal masses initially set at the same longitude on a rough spherical surface. Initial, intermediate and final positions are marked with circles, diamonds and triangles (red for one mass, pink for the other).

where a = 2.0×10–4m–1, b = 4.0×10–4m–1, c = 10–5. The surface is centered on the origin, where the surface bottom is found. The coefficients are such that the slope gradients in x- and ydirections are quite small, in the order of 10–4and steeper along the y-axis.
We select two different masses with m2/m1= 5 and place them initially on the x-axis on the opposite sides of the origin,namely at P01= (4, 0)×102m and P02= (–2, 0)×102m, with the lighter mass at higher altitude. The initial horizontal velocities are opposite, so that the two-mass system has an initial angular momentum around its CoM: they are v01= (0, 50) m/s and v02=(0, –50) m/s. The simulation is computed for t = 200 s, with a time step dt = 0.05 s. Trajectories for the frictionless case are displayed in Fig. 9 over a contour map of the paraboloid. The motion of the masses is a complex combination of the swinging around the paraboloid center, of the rotation around the CoM and of an asymmetric uniform acceleration along the x-axis (due to the coefficient c). It can be observed that the rotation of the lighter mass (mass 1) has a larger radius since the CoM is closer to mass 2.

Fig. 8. Interaction force vs. time for a pair of equal masses initially set at the same longitude over a unit-radius sphere, normalized to mg. The horizontal blue line is the no-friction case. Red, yellow,purple and light-blue curves represent cases respectively with,,,. Simulations are carried out for t = 5T where T is the period of the no-friction case.
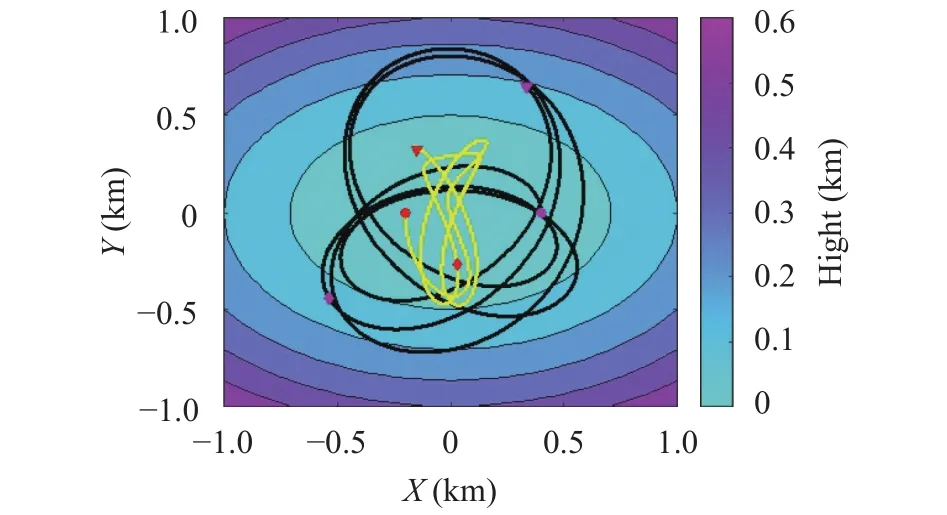
Fig. 9. Trajectories of two different masses sliding over an elliptic paraboloid with no friction: yellow (heavier mass) black (lighter)lines. Initial, intermediate and final positions are shown with circles,diamonds and triangles: red (heavier) and pink (lighter).
In order to have a better understanding of the motion, a plot of the energies time-histories is useful. Figure 10 shows the ratios between potential, and kinetic energies to the total system energy. Since this is a frictionless case, one can observe that there is a perfect balance between the loss (gain) of kinetic and potential energies, as expected.
The exchange between the two forms of energy occurs almost periodically (about 36 s), with about 45%–55% of kinetic energy being converted to potential. The total energy of the CoM exhibits small amplitude oscillations with a double frequency(about 19 s) around the level of 50% of the total energy. This means that the rest of the system energy is taken by the motion of the masses around the CoM, which is the result of our choice for the initial velocities.
When masses move also under the effect of friction, the motion slows down and in the same time span the masses complete less oscillations. This is clear in Fig. 11 where trajectories are displayed. In this study a special attention is given to the interaction force. Its time history is given in Fig. 12 where it is scaled by means of mg with m being the average mass of the particles, i.e..
In the first instants of the motion all time histories are equal,but soon after they differentiate. They start from an initial negative value, which means that the force is attractive. Indeed, due to the initial velocities we selected, the particles, if not linked,would move away from one another, and so the force needs to oppose the tendency to separation. In the no-friction case, the masses keep rotating around the CoM, as we know from Fig. 10.So we can interpret h also as a centripetal force pointing towards the CoM. This explains why h remains negative. The oscillations of h have the same frequency as the CoM total energy oscillations (about 19 s) and magnitude maxima occur together with the minima of the CoM energy, which correspond to the maxima of rotation energy for the masses. It is interesting to ob-serve that in the first stage of the motion the interaction force tends to decrease in magnitude, since the speed of the masses decreases. Figure 14 shows a clear trend, which is larger for larger values of the friction coefficient. It is also worth pointing out that for larger times, h becomes positive, which means that from attractive it transforms to a repulsive force. This occurs when the particles velocity becomes too small and particles, losing angular momentum, tend to converge towards the center of the elliptical paraboloid, and therefore towards one other.
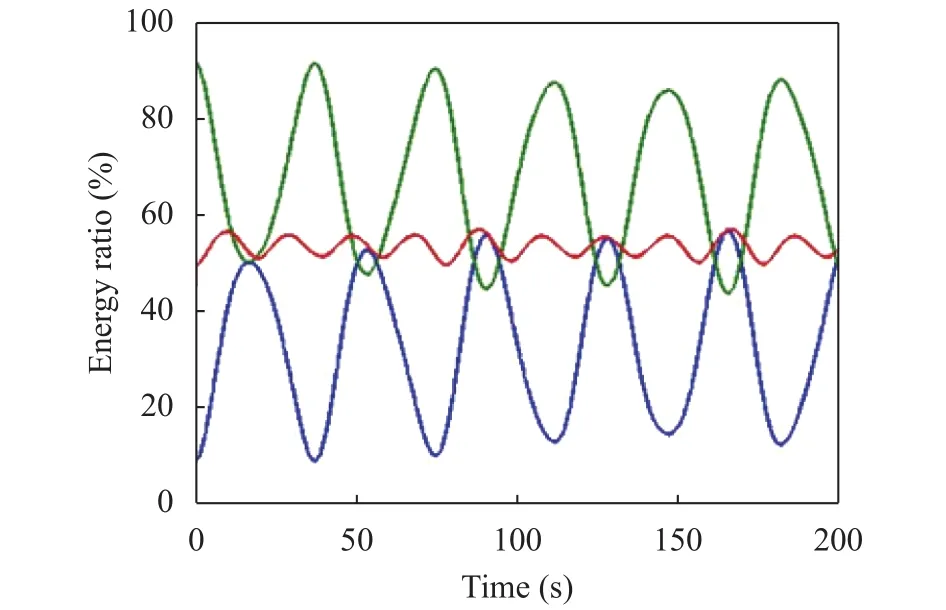
Fig. 10. Energy vs. time for the example shown in Fig. 9. The system energy is partitioned between kinetic (green) and potential (blue)that oscillate with an amplitude that is approximately 50% of the total. The total energy of the CoM (red) oscillates with about double frequency. It swings around 50% of the total energy, which means that about half of the energy is due to the masses rotation around the CoM.
For the sake of completeness, we also show in Fig. 13 the CoM total energy with respect to the total system energy, for different values of the basal friction coefficient. The friction forces have the effect of decelerating the masses. Hence, we do expect that the energy given by the particles rotation around the CoM is smaller as the friction force has stronger magnitude.
This behavior is evident in the trends of Fig. 13, with the purple line representing the bigger friction coefficient and the blue line the no-friction case. In this latter, the CoM total energy is around the 50% of the total system energy while it increases until 80%–90% as the velocities reduce due to the friction forces being larger.
5 Conclusions

Fig. 11. Trajectories for two different masses over an elliptic paraboloid, in case of friction (). See caption of Fig. 9 for further details.
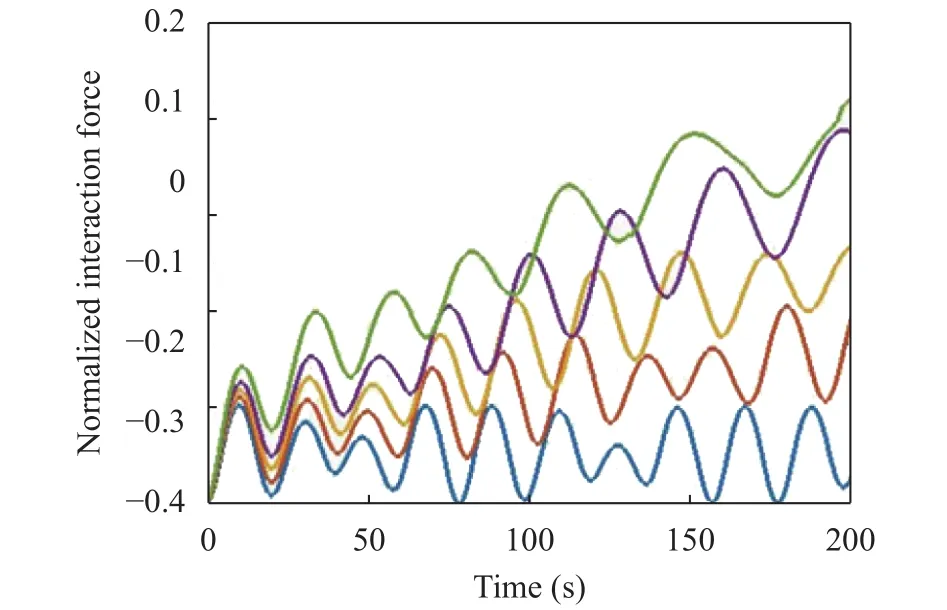
Fig. 12. Interaction force h/(mg) vs. time for different values of the basal friction coefficient. No-friction case (blue) and cases with(red), (orange), (purple),(green).
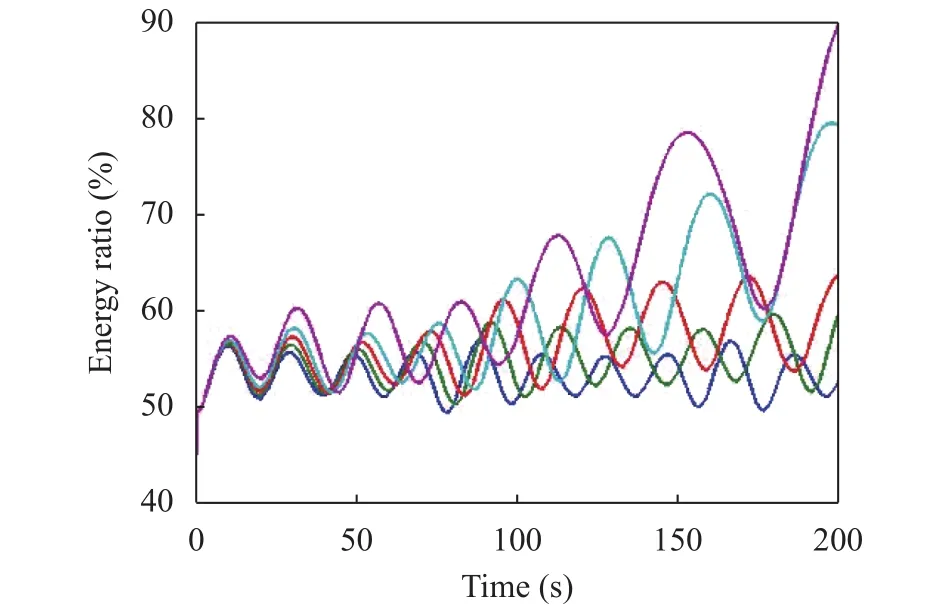
Fig. 13. CoM total energy vs. time for different values of the basal friction coefficient. No-friction case (blue) and cases with(green), (red),, (light-blue), (purple).
This paper is an extension of the study presented in the companion paper [1]. We treat the motion of two particles sliding down analytical surfaces and interacting with each other. The interaction is expressed in the form of a constraint, since we impose that the two masses remain at a constant distance. Such a system can be also seen as a rigid body, formed by two massive elements connected by a rigid inextensible massless rod. To study how the system slides on a surface, in this paper and also in Ref. [1], we proposed two different formulations both based on expressing all the forces acting on the masses including the interaction force and the reaction force exerted by the surface.An alternative classical approach is to formulate the equations of motion for a mechanical system with holonomic constraints [2-5], by using Lagrangian theory and generalized variables. This approach is known to be quite appropriate in case of motion constants such as total system energy or angular momentum [5],but has no advantage in case of dissipative terms like surface friction.
Furthermore, the approach used here allows us to compute all the forces acting on the masses. Our main interest in this paper is the calculation and discussion of the properties of the constant-distance interaction force. To this purpose we have considered a few cases and examples, some of which admit interesting analytical solutions. It has been shown that the force h, that is assumed to lie on the line joining the two masses, can take positive or negative values during the motion. We have interpreted that when the force is positive it acts as a repulsive force,pushing the masses away from one another. Vice versa, when it is negative, it is attractive. Simply, since the force is responsible for keeping the inter-distance constant, it opposes instantaneously any attempts to change it, and attracts masses if they would tend to separate, whereas it repels them if they would tend to come closer.
The magnitude of the force depends on the surface (local gradients) and on the position and velocity of the masses. In the case of equal masses spinning on a spherical surface (Case 1), h is shown to be repulsive and for some combinations of angles(see Fig. 2) to reach values comparable or larger than the weight mg. This remains true also when the masses are different (see Fig. 3), since the force h can take on values larger than the weight of the bigger mass.
Case 2 concerns two equal masses moving with identical motion but on the opposite sides of a sphere (equal colatitude and opposite longitude at any time). The magnitude of h is small compared to the weight. This is due to the fact that the motion takes place close to the bottom of the sphere (=24.35°) and the initial angular distance is also small (=14.04°). Selecting larger initial values forandcould lead to values exceeding the particle weight (see Eqs. (24) and (25)). Interestingly, h oscillates cyclically between a minimum and a maximum value, with the same period as the particles, given by Eq. (21).
Accounting for the bottom friction, leads to solutions where the mechanical energy dissipates progressively, and the masses tend to reach a rest position. The interaction force is seen to tend to a steady final value, that for all examples treated in this paper is positive. This is clear from the graph of Fig. 6 concerning Case 2, but also for plots of Fig. 8 and of Fig. 12 concerning Examples 1 and 2. All these have in common an oscillatory damped behavior with period growing with time, that is superposed to a trend toward the final state. Expectedly, the trend is quicker when the friction coefficient is larger. Example 2 where masses are in the ratio 1 to 5 and the surface is a concave asymmetric paraboloid,shows a very striking behavior of the system that is characterized by two typical periods, as may be seen from Fig. 10. The total energy of the system for a frictionless motion transforms from kinetic to potential and vice versa almost cyclically, with a period of about 36 s. The total energy of the CoM also oscillates but with a much smaller period of about 19 s. Interestingly, the interaction force h oscillates with irregular amplitude almost in phase with the CoM and remains on the negative axis meaning that it is attractive. In a sense the motion is governed by the larger mass that pulls the other behind. When one introduces friction, the interaction force tends to a final value that is positive(Fig. 12), and the total energy of the system tends to coincide with the energy of the CoM (Fig. 13).
All examples treated here regard masses moving on concave surfaces (the interior of a spherical surface or of a paraboloid)where the line joining the masses does not cross the surface.Therefore, the system can be a real mechanical system, where the masses are connected by a real round bar of negligible mass.However, we believe that our model can be applied to concave as well as convex surfaces where the surface reaction can be respectively positive, i.e. pointing upward, or negative, i.e. pointing downward. In this case, our formulation gives an approximate solution.
The understanding of the two-mass scheme is fundamental in order to extend the model to a large number of particles. In fact, our research aims to the development of a model that can simulate rockslides where the volume is partitioned into a set of a large number of massive nodes that interact with each other,while moving on the common sliding surface. Realistic surfaces are complex and usually entail convex and concave regions. The model, of which the present and the companion paper [1] form the basic seminal part, aims to improve the model family where slide bodies are approximated by discrete elements [6, 7], or discrete blocks [8-10] or discrete particles [11, 12].
Appendix A1
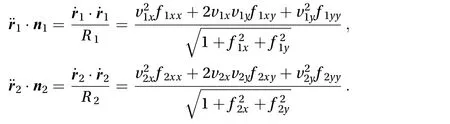
The difference between the accelerations expressed in Eq. (4)is
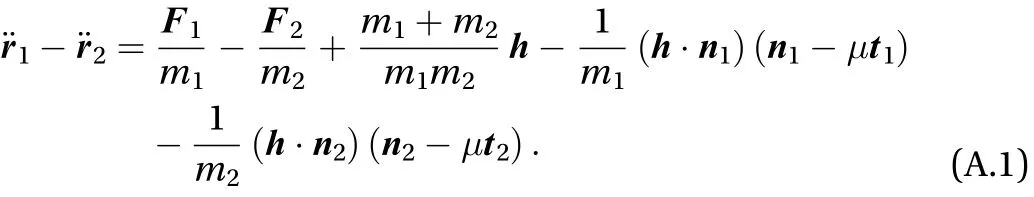
Imposing that the distance between the masses is constant in time implies that
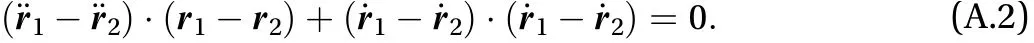
Replacing Eq. (A.1) in Eq. (A.2), we obtain
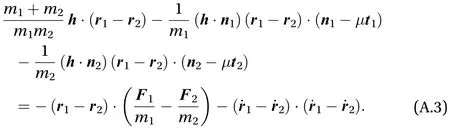
Using Eq. (5) we can write
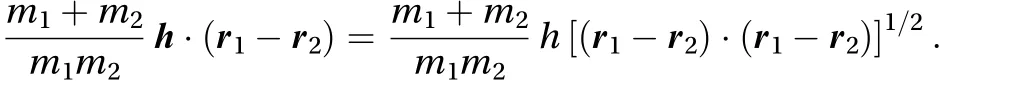
If we expand the second and third terms of Eq. (A.3), we get
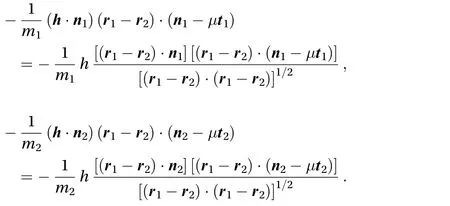
Gathering all together, we obtain the expression for the interaction force h given in Eq. (6).
Appendix A2
The period of a pendulum of length L with maximum angular displacementcan be shown to have the expression

where K(w) is the complete elliptic integral of the first kind defined as
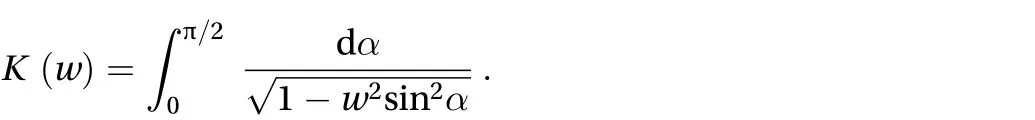
Hence, we can write
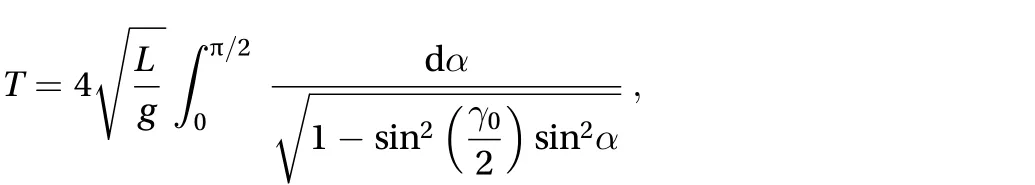
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Particle selectivity of filtering by C. elegans
- The extractable hydrokinetic power from an oscillating membrane-based harvester
- Impact of spray droplets on momentum and heat transport in a turbulent marine atmospheric boundary layer
- A new numerical framework for large-eddy simulation of waves generated by objects piercing water surface
- Numerical solutions for point masses sliding over analytical surfaces: Part 1
- Marangoni liquid film scattering over an extending cylinder
