Marangoni liquid film scattering over an extending cylinder
2019-05-28TzGulSohil
Tz Gul*, M. Sohil
a Department of mathematics, City University of Science and Information Technology, Peshawar, Pakistan
b Department of Mathematics, Govt. Superior Science College Peshawar, Khyber Pakhtunkhwa, Pakistan
Keywords:Marangoni convection Steady flow Thin film spray Stretching cylinder OHAM
A B S T R A C T The impact of the Marangoni convection over the thin film flow on an expanding cylinder has been examined in this study. The diverse effect of the embedded constraints has been detected during the liquid film flow. It has been examined that the behavior of the physical parameters altered after the small intervals and diverse from the traditional approach. The similarity variables have been utilized to alter the basic flow equations into the nonlinear ordinary differential equations. The result of the transformed equations is computed by BVPh 2.0 package. The performance of different constraints, for flow motion and temperature distributions are plotted and conferred. It has been observed that under the Marangoni convection the impact of the physical parameters varies after the point of inflection and the diverse impact of the embedding constraints provide space for the variation of the point of inflection for the desired spray analysis.
The interface lies among the two fluids to bring disparity under the two surface tensions, which is produced by temperature/concentration gradient named as thermal/solutal Marangoni convection. The dissipative fluid layer is known as the Marangoni boundary layer which happens along the fluid or fluid gas interfaces. Because of the surface temperature/focus slope made Marangoni stream, discover the importance in advanced plane design, silicon melt, precious stone development,ignition, synthetic response process, spray and coating, atomic reactors and the thin fluid film.
Moreover, thin film of liquid plays an important role in the spray pattern to sustain the appropriate rate and greatest recital in wire and fiber coating. The friction force is extensively controlled through liquid film indoors the heat transfer spectacles.
Wang [1] studied the phenomena of thin film sprayed on a stretching surface and clarified the problem by utilizing the perturbation solutions. Chen [2] observed the liquid film of the power law model under the Marangoni convection over the unstretched sheet, and used suitable transformations to non-dimensionalize the governing equations and solved the resulting partial differential equations (PDE's) numerically. The impact of the physical parameters has been observed in his study. Ellahi et al. [3] examined the particle shape of the nanoparticles under the effect Marangoni convection. Mahanthesha and Geenisha[4] observed the suspension of dust particles under the influence of Marangoni convection. Al-Shomrani and Gul [5] examined the thin film spray of nanofluid over the expanding cylinder using the slip boundary conditions. They examined the heat transfer enhancement through nanofluid flows. Khan et al.[6] examined the effect of magnetohydrodynamic (MHD) thin film sprayed on an extending cylinder utilizing the nanofluid comprising carbon and aluminum nanoparticles. Thin films are used in many engineering branches and have important applications. Wang et al. [7] studied the mechanical property evaluation of thin film material systems. Razavi et al. [8] investigated the fiber alignment on fracture response of metallic fiber-reinforced adhesive thin films. The modelled problems are usually solved by using the numerical techniques [9-13]. Liao [14] introduced the Homotopy analysis method and BVPh 2.0 package for the solution of high order nonlinear differential equations. This method has the tendency to reduce the residual error and enhance the convergence rate. Gul and Firdous [15] examined the experimental approach for the dispersion of the graphene nanoparticles into the graphene oxide water based nanofluids. They observed the physical outputs through theoretical study of the nanofluid flow amongst binary rotating disks. Gul et al. [16] investigated the liquid film flow over an enlarging sheet under the influence of entropy regime using the homotopy analysis method (HAM) technique. HAM method is frequently used for the various mathematical models [17-23].
The Marangoni convection effect over the boundary layer flow exist in the literature using varieties of mathematical models with applications. The objective of this research is to explore the Marangoni convection effect on the thin film spray over an extending cylinder. It has been observed that the impact of the physical parameters varies under the Marangoni convection and different from the traditional approach. The size of the film and spray rate under the applied surface tension has been calculated from the stabilized results. Moreover, the suitable range of the physical parameters for the proposed problem has been calculated using the BVPh 2.0 package [14-23]. All the outputs have been displayed and discussed.
The thin film spray over a stretching cylinder of radiusis considered in the two dimensionalcoordinate system. The radii a and b of the cylinder and liquid film thickness are along the radial direction such that. The film thickness is represented byandis the extending velocity towards the Z-axis. The ambient temperature is denoted bya nd the temperature transformation is defined asAll otherassumptions for the spray patterns are same as Refs. [1,5, 6]. The basic flow equations are conventional as
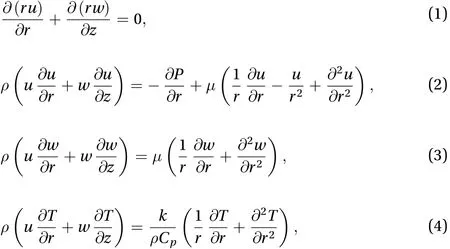
The appropriate boundary conditions are
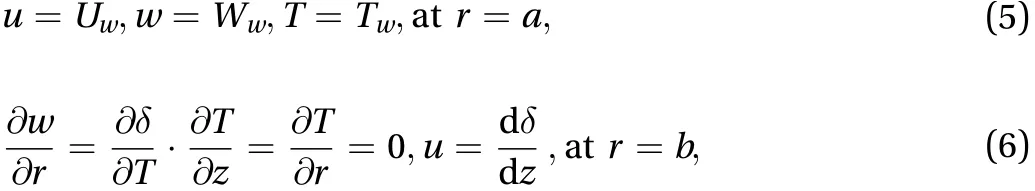

The temperature at the external surface of the liquid film is denoted by.is reference temperature as.
The similarity variables satisfied as Refs. [1, 5, 6, 18, 21] and displayed as
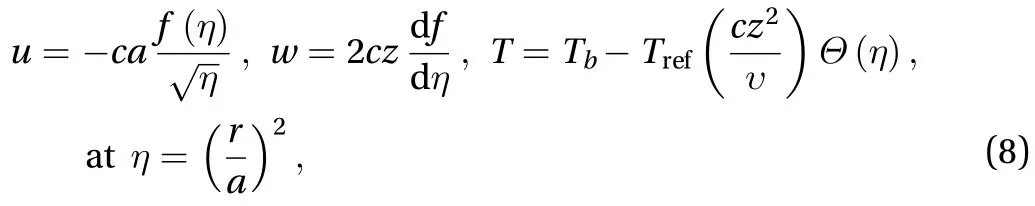
and

is the exterior radius of the liquid film at b.
The similarity variables in Eq. (8) are inserted in Eqs. (1-6),the dimensionless Eqs. (2, 3) become
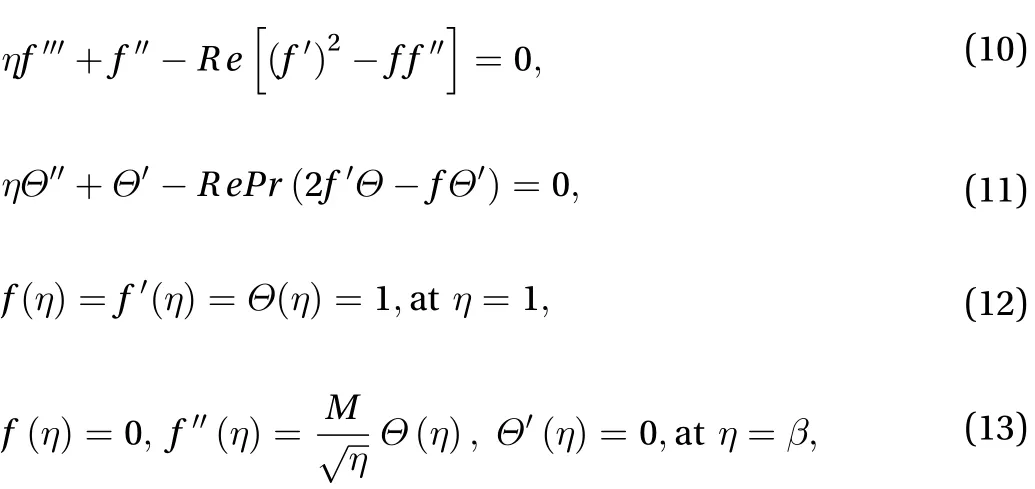
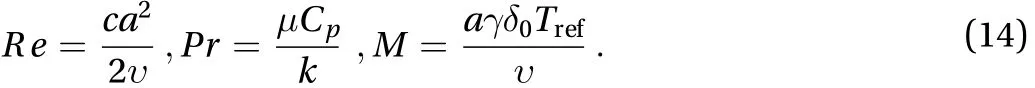
Here, M, Pr, and Re represent the Marangoni constraint Prandtl number and Reynolds number. The similarity variables in Eq. (8) are utilizing in Eq. (3) to obtain the pressure term as

The transformed shear stress on the film exterior portion is

The shear stress on the wall is

The deposition velocity V is written as [1, 5, 6]


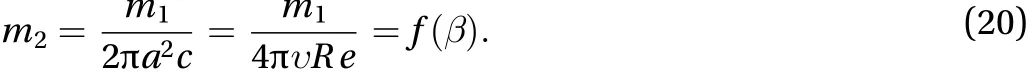
The local skin friction and Nusselt number for the considered flow problem are defined as [5, 6, 21]
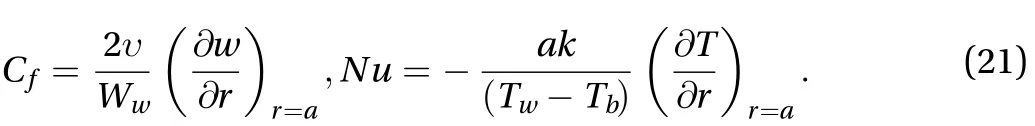
The non-dimensional forms for the above mentioned physical properties are
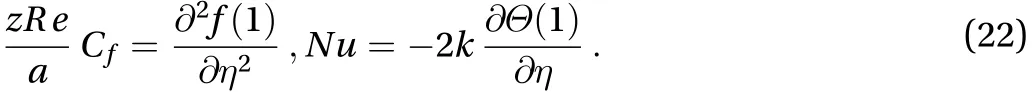
The solution of the modeled problems Eqs. (10, 11), under the initial and boundary conditions Eqs. (12, 13) using the optimal homotopy asymptotic method (OHAM) technique [14-16]have been utilized. The initial guesses have been calculated from the linear operators as
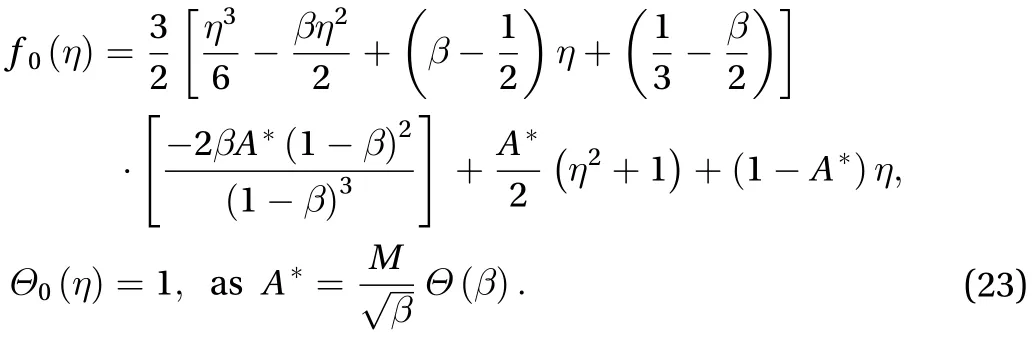
The initial guesses for the velocity and temperature profiles,which satisfy the physical conditions Eqs. (12, 13) have been calculated from the defined linear operators as

The general solution of the linear operators is established as
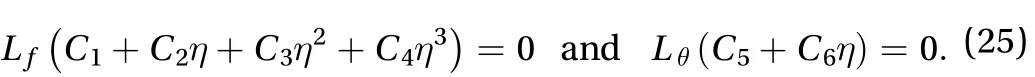
The concept of the average squared residual errors applying the BVPh 2.0 package as defined by Liao [14] to find out the stable convergent solution of the problem has been promoted.
The Eqs. (10, 11) with the physical conditions in Eqs. (12, 13)of the proposed problems are written as,

The combined square residual error is shown as

The total square residual errorin the form of auxiliary parameters has been shown in Fig. 1. The outputs of the optimal convergence controlling constraintsandhave beenachieved from the 20thorder OHAM approximation for the velocity and temperature profiles respectively.
Thin film spray on the surface of an enlarging cylinder under the influence of Marangoni convection has been examined. The formation of the proposed problem has been revealed in Fig. 1.The results of the model problem has been attained through the OHAM technique. The total square residual has been detected and shown in Fig. 2. This method has the tendency to minimize the residual error with the increasing order of approximations.The recent approximations have been used up to the 20thorder.The deviations have been observed in the effect of the physical parameters after the small intervals. The variable thickness of the thin film spray mainly effected due to the Marangoni convection. The diverse effect of the modeled constraints on the fluid motion (spray), temperature and pressure fields have been de-picted in Figs. 3–9.
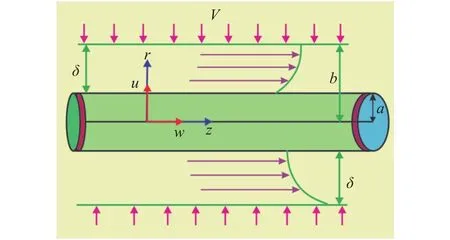
Fig. 1. Geometry of the proposed problem for the thin film spray over a stretching cylinder.
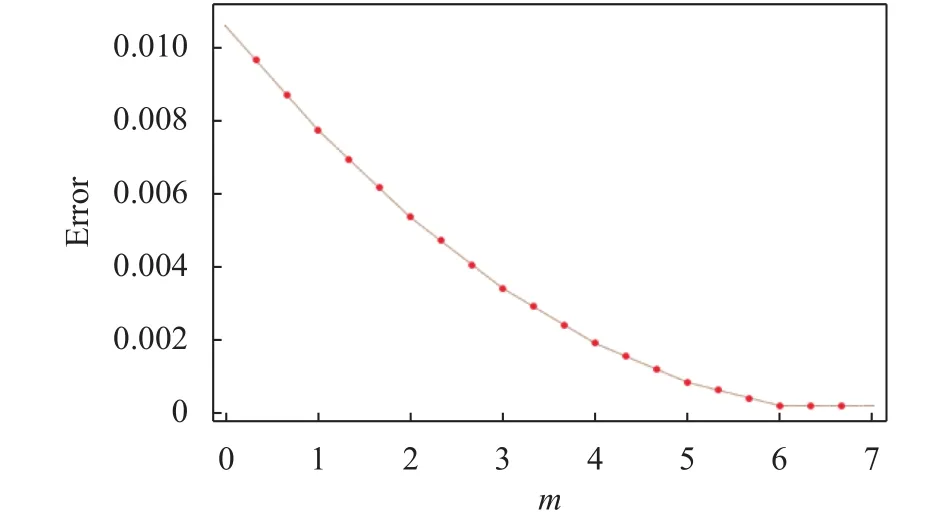
Fig. 2. The total square residual error for the proposed problem.
The impact of the physical parameters varies due to the Marangoni convection like in the published work [1, 5, 6, 18, 21]the larger amount of the film thickness reduces the velocity field.In fact, the increases thickness of the thin film enhances the friction force to decline the spray. In the recent research due to the Marangoni convection the increasing amount of the thickness parameter enhances the flow motion near the cylinder surface and decline the flow motion after the critical point. This show that the spray phenomena varies in short interval with the variation of the film thickness and it is happening only in the existence of Marangoni convection. The increasing amount of the Reynolds numbercommonly reduces the flow field. Physically, Reynolds number expresses the ratio among the inertia forces and viscous forces and the larger amount of the Reynolds number boosted the inertial force and consequently the spray phenomenon disrupted, but the strong Marangoni convection stops this decline for a while and enhancing the flow motion near the wall surface as shown in Fig. 4 and after the point of inflection the flow motion declines. It has been observed that Marangoni convection opposes the Reynolds number near the wall surface and facilitate the film spray. The impact of the Reynolds numberversus temperature distributionhas been shown in Fig. 5.
The increasing amount of the Reynolds numberenhances the temperature profile and the effect is almost as in Refs. [1, 5, 6, 18, 21]. The larger values of the film thickness parameterreduce the heat transfer rate and enhances the cooling effect to decline the temperature distribution near the cylinder surface as shown in Fig. 6, and same as in the published work, but in the presence of Marangoni convection this effect change away from the wall surface and improves the temperature field. It has been observed that the Marangoni Convection controlling the increasing thickness effect away from the cylinder surface.

Fig. 3. Influence of on .

Fig. 4. Influence of on.

Fig. 5. Influence of on.

Fig. 6. Influence of on.
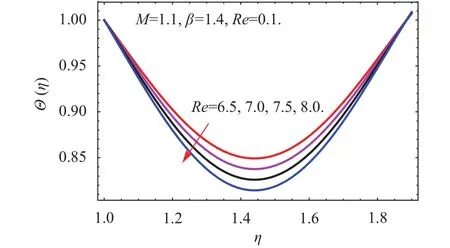
Fig. 7. Influence of Pr on.
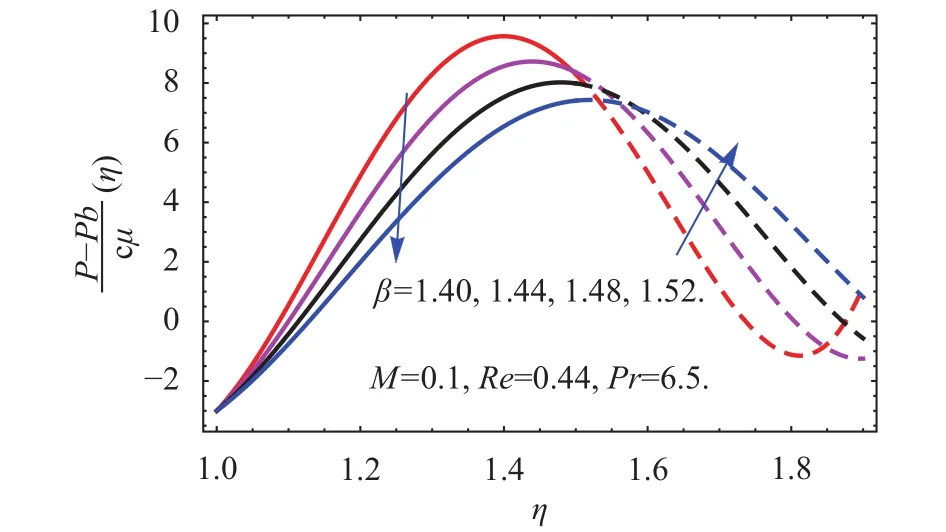
Fig. 8. Influence of on the pressure distribution.
Similarly, the larger amount of the Prandtl numberenhances the thickness of the thermal boundary layer and as a result the temperature profile decline as depicted in Fig. 7.
The pressure term has an important connection during spray pattern. Figure 8 specifies that pressure distribution declined for the greater quantity of the thickness constraintand due to the Marangoni convection this effect is opposite of the published work [1, 5, 6, 18, 21]. The effect changes away the cylinder surface and same as Refs. [1, 5, 6, 18, 21]. Physically, more pressure is required for the thick boundary layer as compared to the thinning liquids during spray phenomenon.
The effect of Reynold number on pressure profile is depicted by Fig. 9. The increasing amount of the Reynolds number improves the inertial forces which reduces the pressure distribution. Due to Marangoni convection the pressure distribution increases at very small level near the mid of the interval and again decline. It has been observed that the strong Marangoni convection interrupt the actual behavior of the physical parameters and this effect is very important for the limitation of the physical parameters during the uniform spray. The thickness parameterand Reynolds number Re relation is shown in the contour Fig. 10. The small value ofmaintaining the smooth relation among theand Re at, but for the greater amount ofthe physical parametersand Re are strongly affected as exposed in Fig. 11. Clearly, the higher values of the Marangoni convection parameter instable the film thicknessand.
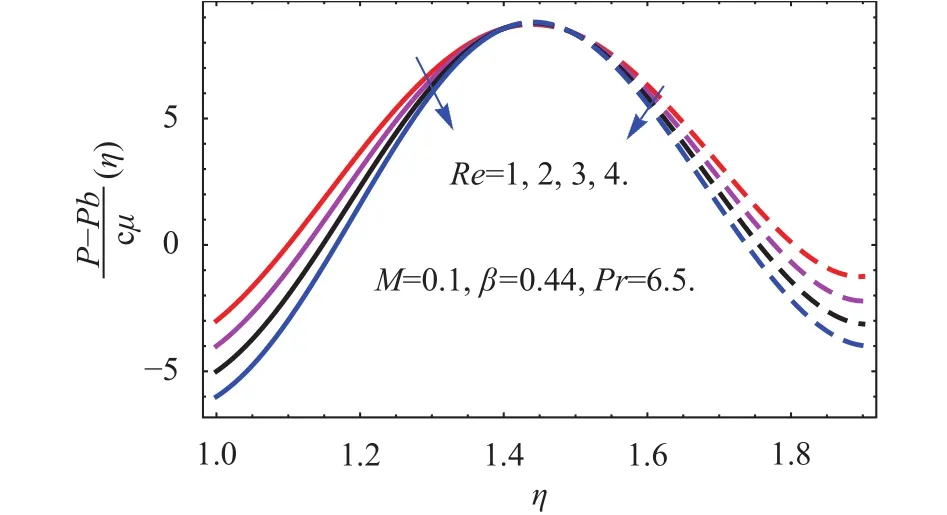
Fig. 9. Influence of Re on the pressure distribution.
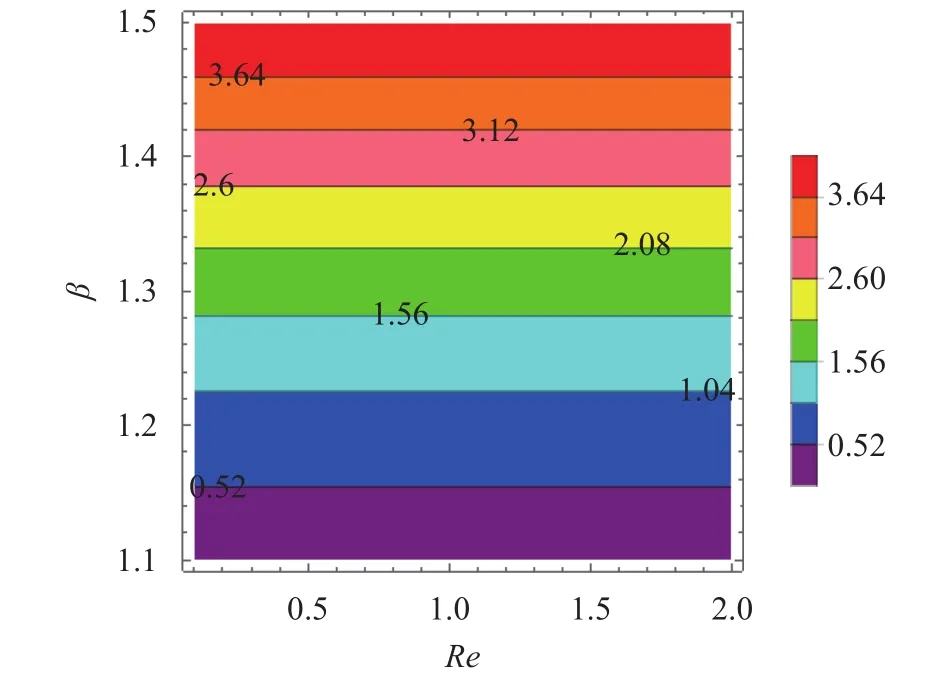
Fig. 10. Contour representation of versus Re.
The total square residual error has been calculated from the velocity and temperature profiles and shown in Table. 1.
The impact of the Reynolds number Re and film thickness parameterversus the local skin friction is examined in Table 2. The larger quantities of the Re andrises the skin friction coefficient. In fact, the larger values of these parameters enhancing the resistance force and consequently the skin friction increases.
The influence of the Pr and thickness parameterversus the Nusselt number is scrutinized in Table 3. The larger amount of these parameters enhances the cooling effect. Clearly the thermal boundary layer enhances with larger quantities of these parameters as mentioned previously and as a result the cooling effect upsurges.
The thin film spray on an extending cylinder under the influence of Marangoni convection has been scrutinized in this research. The solution of the modeled nonlinear differential equations has been obtained through OHAM technique. The absolute total residual error has been calculated for the flow field.The pressure distribution is also necessary for the uniform spray coating and has been observed in this research. The diverse effect of the physical parameters has been observed.
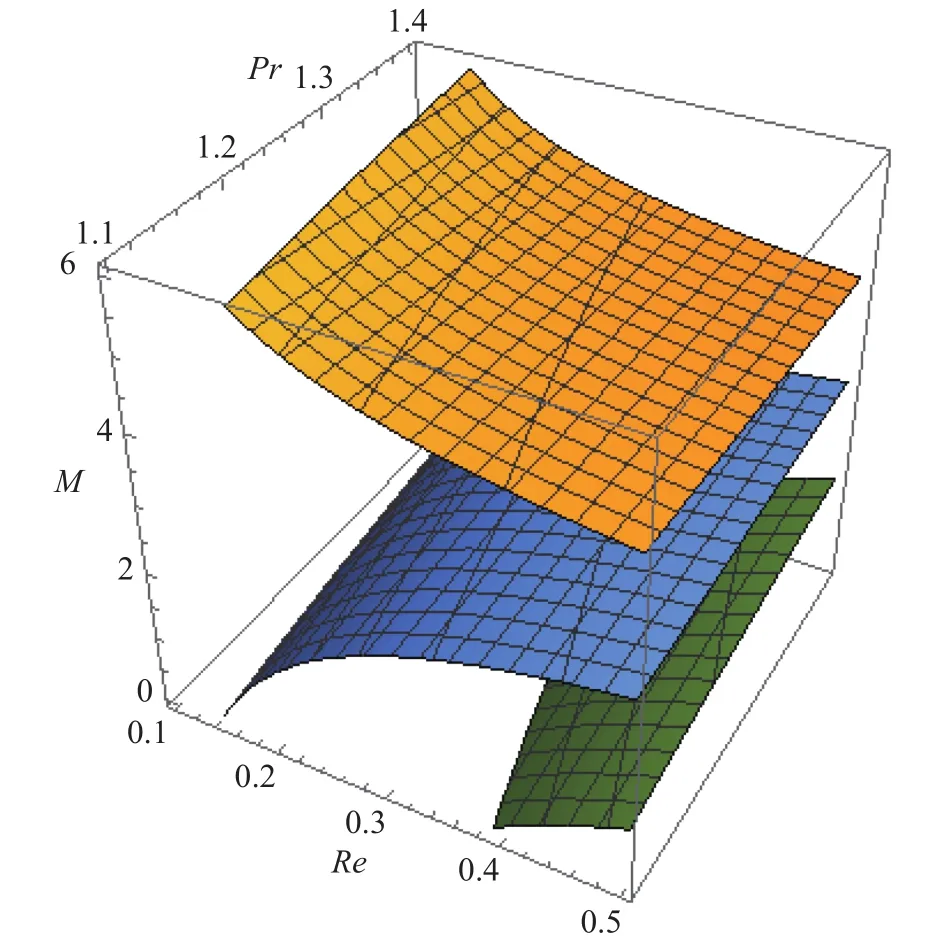
Fig. 11. 3D Contour representation of the parameter and Re.
Table 1 Individual averaged squared residual errors for the velocity and temperature profiles using the BVPh 2.0 package proposed by Liao [8] when.
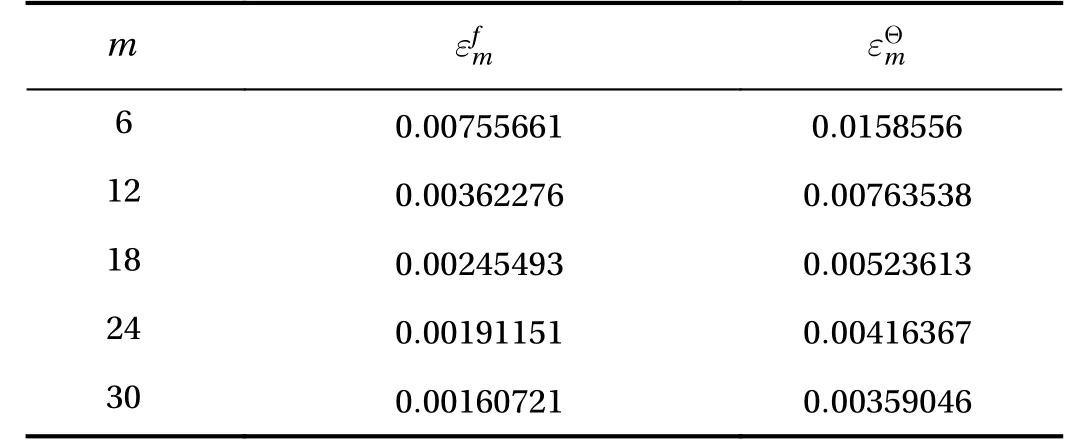
Table 1 Individual averaged squared residual errors for the velocity and temperature profiles using the BVPh 2.0 package proposed by Liao [8] when.
?
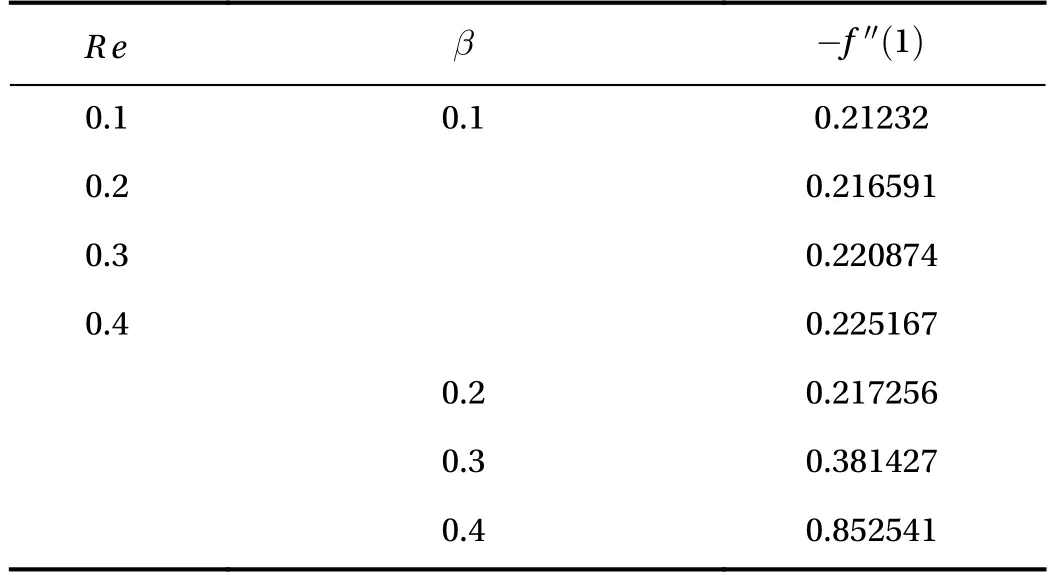
Table 2 Exhibits the numerical values for the skin friction coefficient for different physical parameters.
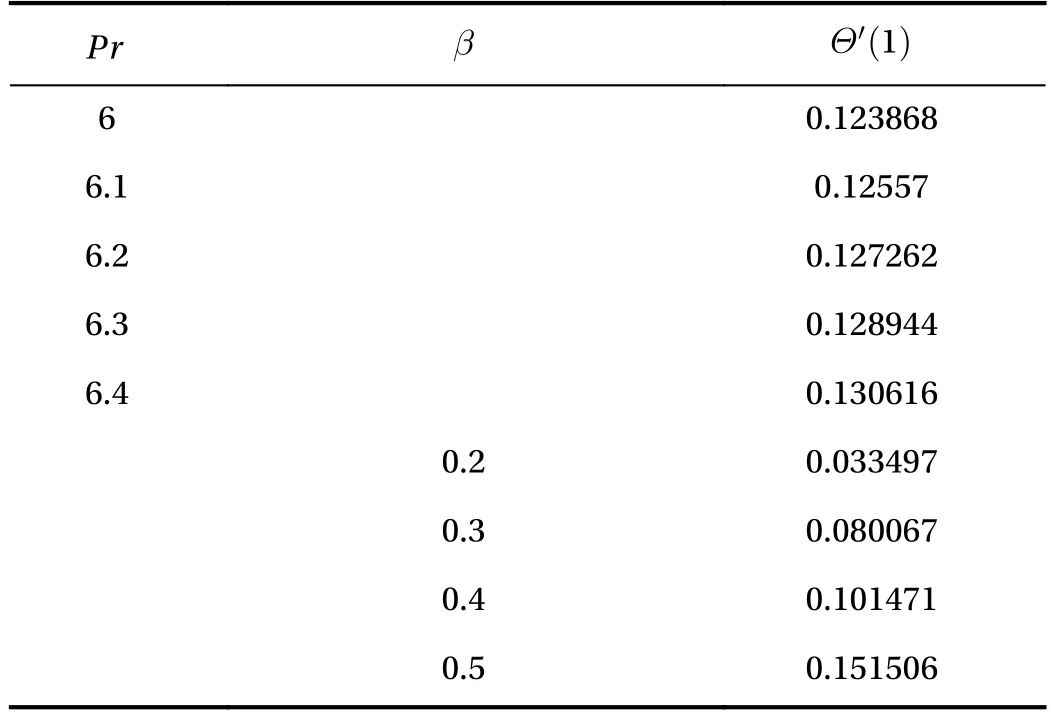
Table 3 Exhibits the numerical values of a local Nusselt number of different physical parameters.
It has been observed that under the Marangoni convection the increasing amount of the thickness parameter enhances the flow motion near the cylinder surface and decline the flow motion after the point of inflection.
The vigorous Marangoni convection interrupts the Reynolds number effect and decline the spray phenomena for a while and enhancing the flow motion near the wall surface. The pressure distribution declined for the greater amount ofand due to the Marangoni convection, this effect is opposite away the cylinder surface. The diverse impact of the physical parameters under the Marangoni convection provides space for the variation of the point of inflection for the desired spray analysis.
杂志排行
Theoretical & Applied Mechanics Letters的其它文章
- Particle selectivity of filtering by C. elegans
- The extractable hydrokinetic power from an oscillating membrane-based harvester
- Impact of spray droplets on momentum and heat transport in a turbulent marine atmospheric boundary layer
- A new numerical framework for large-eddy simulation of waves generated by objects piercing water surface
- Numerical solutions for point masses sliding over analytical surfaces: Part 1
- Numerical solutions for point masses sliding over analytical surfaces: Part 2
